Geometric topology (object)
Encyclopedia
In mathematics
, the geometric topology is a topology
one can put on the set H of hyperbolic 3-manifold
s of finite volume. Convergence in this topology is a crucial ingredient of hyperbolic Dehn surgery
, a fundamental tool in the theory of hyperbolic 3-manifolds.
The following is a definition due to Troels Jorgensen:
There is an alternate definition due to Mikhail Gromov. Gromov's topology utilizes the Gromov-Hausdorff metric and is defined on pointed hyperbolic 3-manifolds. One essentially considers better and better bi-Lipschitz homeomorphisms on larger and larger balls. This results in the same notion of convergence as above as the thick part is always connected; thus, a large ball will eventually encompass all of the thick part.
As a further refinement, Gromov's metric can also be defined on framed hyperbolic 3-manifolds. This gives nothing new but this space can be explicitly identified with torsion-free Kleinian group
s with the Chabauty topology
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the geometric topology is a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
one can put on the set H of hyperbolic 3-manifold
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
s of finite volume. Convergence in this topology is a crucial ingredient of hyperbolic Dehn surgery
Hyperbolic Dehn surgery
In mathematics, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifolds from a given cusped hyperbolic 3-manifold...
, a fundamental tool in the theory of hyperbolic 3-manifolds.
The following is a definition due to Troels Jorgensen:
- A sequence
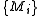in H converges to M in H if there are
- a sequence of positive real numbers
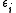converging to 0, and - a sequence of
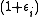-bi-Lipschitz diffeomorphisms 
- where the domains and ranges of the maps are the
-thick parts of either the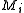 
's or M.
There is an alternate definition due to Mikhail Gromov. Gromov's topology utilizes the Gromov-Hausdorff metric and is defined on pointed hyperbolic 3-manifolds. One essentially considers better and better bi-Lipschitz homeomorphisms on larger and larger balls. This results in the same notion of convergence as above as the thick part is always connected; thus, a large ball will eventually encompass all of the thick part.
As a further refinement, Gromov's metric can also be defined on framed hyperbolic 3-manifolds. This gives nothing new but this space can be explicitly identified with torsion-free Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s with the Chabauty topology
Chabauty topology
In mathematics, the Chabauty topology is a certain topological structure introduced in 1950 by Claude Chabauty, on the set of all closed subgroups of a locally compact group G....
.