
Geometric genus
Encyclopedia
In algebraic geometry
, the geometric genus is a basic birational invariant
pg of algebraic varieties and complex manifold
s.
s as the Hodge number hn,0 (equal to h0,n by Serre duality
), that is, the dimension of the canonical linear system.
In other words for a variety V of complex dimension
n it is the number of linearly independent holomorphic n-forms
to be found on V. This definition, as the dimension of
then carries over to any base field
, when Ω is taken to be the sheaf of Kähler differential
s and the power is the (top) exterior power, the canonical line bundle
.
The geometric genus is the first invariant pg = P1 of a sequence of invariants Pn called the plurigenera.
The notion of genus features prominently in the statement of the Riemann-Roch theorem (see also Riemann-Roch theorem for algebraic curves) and of the Riemann-Hurwitz formula
.
If C is an irreducible (and smooth) hypersurface in the projective plane
cut out by a polynomial equation of degree d, then its normal line bundle is the Serre twisting sheaf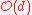 , so by the adjunction formula, the canonical line bundle of C is given by
, so by the adjunction formula, the canonical line bundle of C is given by 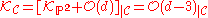 .
.
is the geometric genus of the normalization C′. That is, since the mapping
is birational, the definition is extended by birational invariance.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the geometric genus is a basic birational invariant
Birational invariant
In algebraic geometry, a birational invariant is a quantity or object that is well-defined on a birational equivalence class of algebraic varieties...
pg of algebraic varieties and complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s.
Definition
The geometric genus can be defined for non-singular complex projective varieties and more generally for complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s as the Hodge number hn,0 (equal to h0,n by Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
), that is, the dimension of the canonical linear system.
In other words for a variety V of complex dimension
Complex dimension
In mathematics, complex dimension usually refers to the dimension of a complex manifold M, or complex algebraic variety V. If the complex dimension is d, the real dimension will be 2d...
n it is the number of linearly independent holomorphic n-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
to be found on V. This definition, as the dimension of
- H0(V,Ωn)
then carries over to any base field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, when Ω is taken to be the sheaf of Kähler differential
Kähler differential
In mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
s and the power is the (top) exterior power, the canonical line bundle
Canonical bundle
In mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
.
The geometric genus is the first invariant pg = P1 of a sequence of invariants Pn called the plurigenera.
The case of curves
In the case of complex varieties, (the complex loci of) non-singular curves are Riemann surfaces. The algebraic definition of genus agrees with the topological notion. On a nonsingular curve, the canonical line bundle has degree 2g-2.The notion of genus features prominently in the statement of the Riemann-Roch theorem (see also Riemann-Roch theorem for algebraic curves) and of the Riemann-Hurwitz formula
Riemann-Hurwitz formula
In mathematics, the Riemann–Hurwitz formula, named after Bernhard Riemann and Adolf Hurwitz, describes the relationship of the Euler characteristics of two surfaces when one is a ramified covering of the other. It therefore connects ramification with algebraic topology, in this case...
.
If C is an irreducible (and smooth) hypersurface in the projective plane
Algebraic geometry of projective spaces
Projective spaces play a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of those spaces.- Homogeneous polynomial ideals:...
cut out by a polynomial equation of degree d, then its normal line bundle is the Serre twisting sheaf
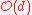 , so by the adjunction formula, the canonical line bundle of C is given by
, so by the adjunction formula, the canonical line bundle of C is given by 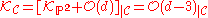 .
.Genus of singular varieties
The definition of geometric genus is carried over classically to singular curves C, by decreeing that- pg(C)
is the geometric genus of the normalization C′. That is, since the mapping
- C′ → C
is birational, the definition is extended by birational invariance.
See also
- Genus (mathematics)Genus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
- Arithmetic genusArithmetic genusIn mathematics, the arithmetic genus of an algebraic variety is one of some possible generalizations of the genus of an algebraic curve or Riemann surface.The arithmetic genus of a projective complex manifold...
- Invariants of surfaces

