Generic-case complexity
Encyclopedia
Generic-case complexity is a subfield of computational complexity theory
that studies the complexity of computational problems on "most inputs".
Generic-case complexity is a way of measuring the complexity of a computational problem
by neglecting a small set of
unrepresentative inputs and considering worst-case complexity on the rest.
Small is defined in terms of asymptotic density.
The apparent efficacy of generic case complexity is because for a wide variety of concrete computational problems, the most difficult instances seem to be rare. Typical instances are relatively easy.
This approach to complexity originated in combinatorial group theory
, which has a computational tradition going back to the beginning of the last century.
The notion of generic complexity was introduced in
where authors showed that for a large class of finitely generated groups the generic time complexity of some classical decision problems from combinatorial group theory, namely the word problem
, conjugacy problem
and membership problem, are linear.
A detailed introduction of generic case complexity can be found in the surveys
,
.
Definition 1. A size function on I is a map with infinite range.
with infinite range.
The ball of radius n is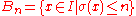 .
.
If the inputs are coded as strings over a finite alphabet, size might be the string length.
Let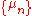 be an ensemble of probability distributions where
be an ensemble of probability distributions where 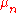
is a probability distribution
on .
.
If the balls are finite, then each
are finite, then each 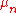 can be taken to
can be taken to
be the equiprobable distribution which is the most common case. Notice that only finitely many
 's can be empty or have
's can be empty or have 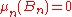 ; we ignore them.
; we ignore them.
Definition 2. The asymptotic density of a subset is
is
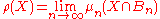 when this limit exists.
when this limit exists.
When the balls are finite and
are finite and 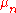 is the equiprobable measure,
is the equiprobable measure,
In this case it is often convenient to use spheres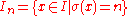 instead of balls and
instead of balls and
define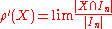 . An argument using Stolz theorem shows that
. An argument using Stolz theorem shows that 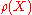
exists if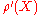 does, and in that case they are equal.
does, and in that case they are equal.
Definition 3 is generic if
is generic if 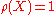 and negligible if
and negligible if 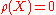 .
.
X is exponentially (superpolynomially) generic if the convergence to the limit in Definition 2 is exponentially (superpolynomially) fast, etc.
A generic subset X is asymptotically large. Whether X appears large in practice depends
on how fast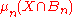 converges to 1. Superpolynomial convergence seems to be fast enough.
converges to 1. Superpolynomial convergence seems to be fast enough.
is in GenP (generically polynomial time) if it never gives incorrect answers and if it
gives correct answers in polynomial time on a generic set of inputs. A problem is in GenP if it
admits an algorithm in GenP. Likewise for GenL (generically linear time), GenE (generically
exponential time with a linear exponent) GenExp (generically exponential time), etc.
ExpGenP is the subclass of GenP for which the relevant generic set is exponentially generic.
More generally for any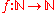 we can define the class Gen(f) corresponding to
we can define the class Gen(f) corresponding to
time complexity
O(f) on a generic set of input.
Definition 5. An algorithm solves a problem generically if it never gives incorrect answers and if it gives correct answers on a generic set of inputs. A problem is generically solvable if it is solved generically by some algorithm.
The situation for two-sided tape is unknown. However, there is a kind of lower bound for machines of both types.
The halting problem is not in ExpGenP for any model of Turing machine,
Presburger arithmetic
NP complete problems
One way functions
Public-key cryptography
A series of articles, is devoted to cryptanalysis of the Anshel–Anshel–Goldfeld key exchange protocol,
whose security is based on assumptions about the braid group
. This series culminates in which applies techniques from
generic case complexity to obtain a complete analysis of the length based attack and the
conditions under which it works. The generic point of view also suggests a kind of new
attack called the quotient attack, and a more secure version of the Anshel–Anshel–Goldfeld protocol.
List of general theoretical results
Theorem 1 Let I be the set of all Turing machines. If F is a subset of the set of all
partial computable function from to itself such that F and its complement are both non-empty,
to itself such that F and its complement are both non-empty,
then the problem of deciding whether or not a given Turing machine computes a function from
F is not decidable on any exponentially generic subset of I.
Theorem 2 The set of formal languages which are generically computable has measure zero.
Theorem 3 There is an infinite hierarchy of generic complexity classes. More precisely
for a proper complexity function f, .
.
there are also generic case complete problems. The arguments in the generic case are similar to
those in the average case, and the generic case complete problem is also average case complete.
It is the distributional bounded halting problem.
Theorem 4 There is a notion of generic-polynomial-time reduction with respect to
which the distributional bounded halting problem is complete within class of distributional NP problems.
Almost polynomial time
Meyer and Paterson define an algorithm to be almost polynomial time, or APT, if it halts
within p(n) steps on all but p(n) inputs of size n. Clearly APT algorithms are included in our
class GenP. We have seen several NP complete problems in GenP, but Meyer and Paterson
show that this is not the case for APT. They prove that an NP complete problem is reducible to
a problem in APT if and only if P = NP. Thus APT seems much more restrictive than GenP.
Average-case complexity
Generic case complexity is similar to average-case complexity
. However there are some significant differences.
Generic case complexity is a direct measure of the performance of an algorithm on most inputs while average case complexity
gives a measure of the balance between easy and difficult instances. In addition Generic-case complexity naturally applies to undecidable problem
s.
Suppose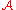 is an algorithm whose time complexity
is an algorithm whose time complexity
, is polynomial on
is polynomial on  average.
average.
What can we infer about the behavior of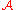 on typical inputs?
on typical inputs?
Example 1 Let I be the set of all words over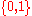 and define the size
and define the size 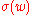 to be word length,
to be word length,
 . Define
. Define 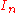 to be the set of words of length n, and assume that each
to be the set of words of length n, and assume that each 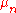 is the equiprobable measure.
is the equiprobable measure.
Suppose that T(w)=n for all but one word in each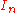 , and
, and  on the exceptional words.
on the exceptional words.
In this example T is certainly polynomial on typical inputs, but T is not polynomial on average. T is in GenP.
Example 2 Keep I and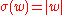 as before, but define
as before, but define 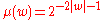 and
and
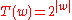 . T is polynomial on average even though it is exponential on typical inputs. T is not in GenP.
. T is polynomial on average even though it is exponential on typical inputs. T is not in GenP.
In these two examples the generic complexity is more closely related to behavior
on typical inputs than average case complexity. Average case complexity measures something
else: the balance between the frequency of difficult instances and the degree of difficulty,.
Roughly speaking an algorithm which is polynomial time on average can have only a subpolynomial
fraction of inputs that require superpolynomial time to compute.
Nevertheless in some cases generic and average case complexity are quite close to each other.
A function is polynomial on
is polynomial on  -average on spheres if there
-average on spheres if there
exists such that
such that 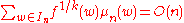 where
where 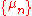
is the ensemble induced by . If f is polynomial on
. If f is polynomial on  -average on spheres, the f is
-average on spheres, the f is
polynomial on -average, and for many distributions the converse holds
-average, and for many distributions the converse holds
Theorem 5 If a function is polynomial on
is polynomial on  -average on spheres then f
-average on spheres then f
is generically polynomial relative to the spherical asymptotic density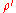 .
.
Theorem 6 Suppose a complete algorithm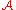 has subexponential time bound T and a partial algorithm
has subexponential time bound T and a partial algorithm 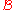
for the same problem is in ExpGenP with respect to the ensemble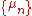 corresponding to a probability measure
corresponding to a probability measure 
on the inputs I for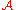 . Then there is a complete algorithm which is
. Then there is a complete algorithm which is  -average time complexity.
-average time complexity.
Errorless heuristic algorithms
In a 2006 paper, Bogdanov and Trevisan came close to defining generic case complexity. Instead of partial algorithms, they consider so-called errorless heuristic algorithms. These are
complete algorithms which may fail by halting with output "?". The class AvgnegP is defined
to consist of all errorless heuristic algorithms A which run in polynomial time and for which the
probability of failure on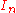 is negligible, i.e., converges superpolynomially fast to 0.
is negligible, i.e., converges superpolynomially fast to 0.
AvgnegP is a subset of GenP. Errorless heuristic algorithms are essentially the same as the algorithms with
benign faults defined by Impagliazzo where polynomial time on average algorithms are
characterized in terms of so-called benign algorithm schemes.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
that studies the complexity of computational problems on "most inputs".
Generic-case complexity is a way of measuring the complexity of a computational problem
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
by neglecting a small set of
unrepresentative inputs and considering worst-case complexity on the rest.
Small is defined in terms of asymptotic density.
The apparent efficacy of generic case complexity is because for a wide variety of concrete computational problems, the most difficult instances seem to be rare. Typical instances are relatively easy.
This approach to complexity originated in combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
, which has a computational tradition going back to the beginning of the last century.
The notion of generic complexity was introduced in
where authors showed that for a large class of finitely generated groups the generic time complexity of some classical decision problems from combinatorial group theory, namely the word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
, conjugacy problem
Conjugacy problem
In abstract algebra, the conjugacy problem for a group G with a given presentation is the decision problem of determining, given two words x and y in G, whether or not they represent conjugate elements of G...
and membership problem, are linear.
A detailed introduction of generic case complexity can be found in the surveys
,
.
Asymptotic density
Let I be an infinite set of inputs for a computational problem.Definition 1. A size function on I is a map
 with infinite range.
with infinite range.The ball of radius n is
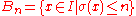 .
.If the inputs are coded as strings over a finite alphabet, size might be the string length.
Let
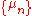 be an ensemble of probability distributions where
be an ensemble of probability distributions where 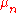
is a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on
 .
.If the balls
 are finite, then each
are finite, then each 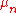 can be taken to
can be taken tobe the equiprobable distribution which is the most common case. Notice that only finitely many
 's can be empty or have
's can be empty or have 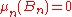 ; we ignore them.
; we ignore them.Definition 2. The asymptotic density of a subset
 is
is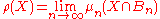 when this limit exists.
when this limit exists.When the balls
 are finite and
are finite and 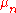 is the equiprobable measure,
is the equiprobable measure,In this case it is often convenient to use spheres
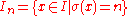 instead of balls and
instead of balls anddefine
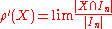 . An argument using Stolz theorem shows that
. An argument using Stolz theorem shows that 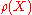
exists if
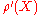 does, and in that case they are equal.
does, and in that case they are equal.Definition 3
 is generic if
is generic if 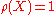 and negligible if
and negligible if 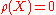 .
.X is exponentially (superpolynomially) generic if the convergence to the limit in Definition 2 is exponentially (superpolynomially) fast, etc.
A generic subset X is asymptotically large. Whether X appears large in practice depends
on how fast
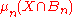 converges to 1. Superpolynomial convergence seems to be fast enough.
converges to 1. Superpolynomial convergence seems to be fast enough.Generic complexity classes
Definition 4 An algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is in GenP (generically polynomial time) if it never gives incorrect answers and if it
gives correct answers in polynomial time on a generic set of inputs. A problem is in GenP if it
admits an algorithm in GenP. Likewise for GenL (generically linear time), GenE (generically
exponential time with a linear exponent) GenExp (generically exponential time), etc.
ExpGenP is the subclass of GenP for which the relevant generic set is exponentially generic.
More generally for any
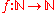 we can define the class Gen(f) corresponding to
we can define the class Gen(f) corresponding totime complexity
Time complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
O(f) on a generic set of input.
Definition 5. An algorithm solves a problem generically if it never gives incorrect answers and if it gives correct answers on a generic set of inputs. A problem is generically solvable if it is solved generically by some algorithm.
Combinatorial group theory problems.
- The famous undecidable problemUndecidable problemIn computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
s: the word, conjugacy and membership decision problems are in generically polynomial.
- The word and conjugacy search problemSearch problemIn computational complexity theory and computability theory, a search problem is a type of computational problem represented by a binary relation...
s are in GenP for all fixed finitely presented groups.
- The well known coset enumerationCoset enumerationIn mathematics, coset enumeration is the problem of counting the cosets of a subgroup H of a group G given in terms of a presentation. As a by-product, one obtains a permutation representation for G on the cosets of H...
procedure admits a computable upper bound on a generic set of inputs.
- The Whitehead algorithm for testing whether or not one element of a free group is mapped to another by an automorphism has an exponential worst case upper bound but runs well in practice. The algorithm is shown to be in GenL.
- The conjugacy problem in HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s can be unsolvable even for free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s. However, it is generically cubic time
The halting problem and the Post correspondence problem.
- The halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
for Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
with one-sided tape is easily decidable most of the time; it is in GenP
The situation for two-sided tape is unknown. However, there is a kind of lower bound for machines of both types.
The halting problem is not in ExpGenP for any model of Turing machine,
- The Post correspondence problemPost correspondence problemThe Post correspondence problem is an undecidable decision problem that was introduced by Emil Post in 1946. Because it is simpler than the halting problem and the Entscheidungsproblem it is often used in proofs of undecidability....
is in ExpGenP.
Presburger arithmetic
The decision problemDecision problemIn computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
for Presburger arithmeticPresburger arithmeticPresburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
admits a double exponential
worst case lower bound and a triple exponential worst case upper bound. The
generic complexity is not known, but it is known that the problem is not in ExpGenP
NP complete problems
As it is well known that NP-complete problems can be easy on average, it is not a surprise that several of them are generically easy too.
- The three satisfiability problem is in ExpGenP
- The subset sum problem is in GenP.
One way functions
There is a generic complexity version of a one-way functionOne-way functionIn computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems...
which yields the same class of functions but allows one to consider different security assumptions than usual.
Public-key cryptography A series of articles, is devoted to cryptanalysis of the Anshel–Anshel–Goldfeld key exchange protocol,
whose security is based on assumptions about the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
. This series culminates in which applies techniques from
generic case complexity to obtain a complete analysis of the length based attack and the
conditions under which it works. The generic point of view also suggests a kind of new
attack called the quotient attack, and a more secure version of the Anshel–Anshel–Goldfeld protocol.
List of general theoretical results
- A famous Rice's theoremRice's theoremIn computability theory, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide whether an algorithm computes a partial function with that property...
states that if F is a subset of the set of partial computable functions from to
to 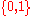 , then unless F or its complement is empty, the problem of deciding whether or not a particular Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, then unless F or its complement is empty, the problem of deciding whether or not a particular Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
computes a function in F is undecidable. The following theorem gives a generic version.
Theorem 1 Let I be the set of all Turing machines. If F is a subset of the set of all
partial computable function from
 to itself such that F and its complement are both non-empty,
to itself such that F and its complement are both non-empty,then the problem of deciding whether or not a given Turing machine computes a function from
F is not decidable on any exponentially generic subset of I.
- The following theorems are from.
Theorem 2 The set of formal languages which are generically computable has measure zero.
Theorem 3 There is an infinite hierarchy of generic complexity classes. More precisely
for a proper complexity function f,
 .
.- The next theorem shows that just as there are average case complete problems within distributional NP problems,
there are also generic case complete problems. The arguments in the generic case are similar to
those in the average case, and the generic case complete problem is also average case complete.
It is the distributional bounded halting problem.
Theorem 4 There is a notion of generic-polynomial-time reduction with respect to
which the distributional bounded halting problem is complete within class of distributional NP problems.
Almost polynomial time
Meyer and Paterson define an algorithm to be almost polynomial time, or APT, if it halts
within p(n) steps on all but p(n) inputs of size n. Clearly APT algorithms are included in our
class GenP. We have seen several NP complete problems in GenP, but Meyer and Paterson
show that this is not the case for APT. They prove that an NP complete problem is reducible to
a problem in APT if and only if P = NP. Thus APT seems much more restrictive than GenP.
Average-case complexity
Generic case complexity is similar to average-case complexity
Average-case complexity
Average-case complexity is a subfield of computational complexity theory that studies the complexity of algorithms on random inputs.The study of average-case complexity has applications in the theory of cryptography....
. However there are some significant differences.
Generic case complexity is a direct measure of the performance of an algorithm on most inputs while average case complexity
gives a measure of the balance between easy and difficult instances. In addition Generic-case complexity naturally applies to undecidable problem
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
s.
Suppose
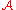 is an algorithm whose time complexity
is an algorithm whose time complexityTime complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
,
 is polynomial on
is polynomial on  average.
average.What can we infer about the behavior of
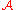 on typical inputs?
on typical inputs?Example 1 Let I be the set of all words over
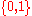 and define the size
and define the size 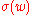 to be word length,
to be word length, . Define
. Define 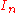 to be the set of words of length n, and assume that each
to be the set of words of length n, and assume that each 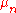 is the equiprobable measure.
is the equiprobable measure.Suppose that T(w)=n for all but one word in each
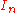 , and
, and  on the exceptional words.
on the exceptional words.In this example T is certainly polynomial on typical inputs, but T is not polynomial on average. T is in GenP.
Example 2 Keep I and
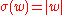 as before, but define
as before, but define 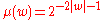 and
and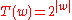 . T is polynomial on average even though it is exponential on typical inputs. T is not in GenP.
. T is polynomial on average even though it is exponential on typical inputs. T is not in GenP.In these two examples the generic complexity is more closely related to behavior
on typical inputs than average case complexity. Average case complexity measures something
else: the balance between the frequency of difficult instances and the degree of difficulty,.
Roughly speaking an algorithm which is polynomial time on average can have only a subpolynomial
fraction of inputs that require superpolynomial time to compute.
Nevertheless in some cases generic and average case complexity are quite close to each other.
A function
 is polynomial on
is polynomial on  -average on spheres if there
-average on spheres if thereexists
 such that
such that 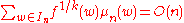 where
where 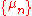
is the ensemble induced by
 . If f is polynomial on
. If f is polynomial on  -average on spheres, the f is
-average on spheres, the f ispolynomial on
 -average, and for many distributions the converse holds
-average, and for many distributions the converse holdsTheorem 5 If a function
 is polynomial on
is polynomial on  -average on spheres then f
-average on spheres then fis generically polynomial relative to the spherical asymptotic density
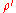 .
.Theorem 6 Suppose a complete algorithm
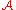 has subexponential time bound T and a partial algorithm
has subexponential time bound T and a partial algorithm 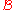
for the same problem is in ExpGenP with respect to the ensemble
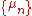 corresponding to a probability measure
corresponding to a probability measure 
on the inputs I for
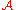 . Then there is a complete algorithm which is
. Then there is a complete algorithm which is  -average time complexity.
-average time complexity.Errorless heuristic algorithms
In a 2006 paper, Bogdanov and Trevisan came close to defining generic case complexity. Instead of partial algorithms, they consider so-called errorless heuristic algorithms. These are
complete algorithms which may fail by halting with output "?". The class AvgnegP is defined
to consist of all errorless heuristic algorithms A which run in polynomial time and for which the
probability of failure on
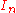 is negligible, i.e., converges superpolynomially fast to 0.
is negligible, i.e., converges superpolynomially fast to 0.AvgnegP is a subset of GenP. Errorless heuristic algorithms are essentially the same as the algorithms with
benign faults defined by Impagliazzo where polynomial time on average algorithms are
characterized in terms of so-called benign algorithm schemes.