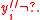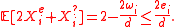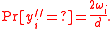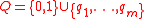Generalized minimum distance decoding
Encyclopedia
In coding theory
, generalized minimum-distance (GMD) decoding provides an efficient algorithm
for decoding concatenated codes, which is based on using an error
s-and-erasures
decoder
for the outer code.
A naive decoding algorithm for concatenated codes can not be an optimal way of decoding because it does not take into account the information that maximum likelihood decoding (MLD) gives. In other words, in the naive algorithm, inner received codewords are treated the same regardless of the difference between their hamming distance
s. Intuitively, the outer decoder should place higher confidence in symbols whose inner encodings
are close to the received word. David Forney
in 1966 devised a better algorithm called generalized minimum distance (GMD) decoding which makes use of those information better. This method is achieved by measuring confidence of each received codeword, and erasing symbols whose confidence is below a desired value. And GMD decoding algorithm was one of the first examples of soft-decision decoder
s. We will present three versions of the GMD decoding algorithm. The first two will be randomized algorithm
s while the last one will be a deterministic algorithm
.
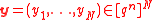which corrupted by noisy channel. The following is the algorithm description for the general case. In this algorithm, we can decode y by just declaring an erasure at every bad position and running the errors and erasure decoding algorithm for 
on the resulting vector.
Randomized_Decoder
Given :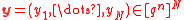
.
Theorem 1. Let y be a received word such that there exists a codeword
such that 
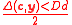. Then the deterministic GMD algorithm outputs 
.
Note that a naive decoding algorithm for concatenated codes can correct up to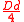
errors.
Lemma 1. Let the assumption in Theorem 1 hold. And if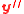
has 
errors and 
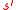erasures(when compared with 
) after Step 1, then 
.
If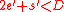
, then the algorithm in Step 2 will output 
. The lemma above says that in expectation, this is indeed the case. Note that this is not enough to prove Theorem 1, but can be crucial in developing future variations of the algorithm.
Proof of lemma 1. For every
, define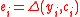 
. This implies that
Next for every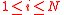
, we define two indicator variables:
and
and
We claim that we are done if we can show that for every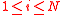
:
Clearly, by definition
and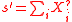 
. Further, by the linearity
of expectation, we get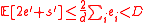
. We consider two cases to prove (2) : 
block is correctly decoded(Case 1), 
block is incorrectly decoded(Case 2)
Case 1: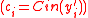
Note that if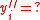
then 
, and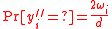 
implies
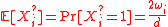, and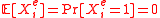 
.
Further, by definition we have
Case 2:
In this case,
Since
, 
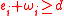. This follows another case analysis when 
or not.
Finally, this implies
In the following sections, we will finally show that the deterministic version of the algorithm above can do unique decoding of
up to half its design distance.
for each
. Now we come up with another randomized version of the GMD algorithm that uses the same randomness for every 
. This idea follows the algorithm below.
Modified_Randomized_Decoder
Given :
, pick 
at random. Then every for every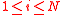 
:
For the proof of Lemma 1
, we only use the randomness to show that
In this version of the GMD algorithm, we note that
The second equality above follows from the choice of
. The proof of Lemma 1 can be also used to show 
< 
for version2 of GMD.
In the next section, we will see how to get a deterministic version of the GMD algorithm by choosing θ from a polynomially sized set as opposed to the current infinite set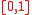
.
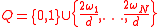. Since for each 
, we have
where
for some 
. Note that for every 
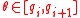, the step 1 of the second version of randomized algorithm outputs the same 
. Thus, we need to consider all possible value of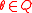 
. This gives the deterministic algorithm below.
Deterministic_Decoder
Given :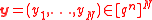
, for every 
, repeat the following.
Every loop of 1~4 can be run in polynomial time, the algorithm above can also be computed in polynomial time.
Specifically, each call to an errors and erasures decoder of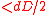
errors takes 
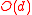time. Finally, the runtime of the algorithm above is 
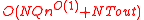where 
is the running time of the outer errors and erasures decoder.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, generalized minimum-distance (GMD) decoding provides an efficient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for decoding concatenated codes, which is based on using an error
Error
The word error entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge...
s-and-erasures
Erasure code
In information theory, an erasure code is a forward error correction code for the binary erasure channel, which transforms a message of k symbols into a longer message with n symbols such that the original message can be recovered from a subset of the n symbols...
decoder
Decoder
A decoder is a device which does the reverse operation of an encoder, undoing the encoding so that the original information can be retrieved. The same method used to encode is usually just reversed in order to decode...
for the outer code.
A naive decoding algorithm for concatenated codes can not be an optimal way of decoding because it does not take into account the information that maximum likelihood decoding (MLD) gives. In other words, in the naive algorithm, inner received codewords are treated the same regardless of the difference between their hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
s. Intuitively, the outer decoder should place higher confidence in symbols whose inner encodings
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
are close to the received word. David Forney
David Forney
George David "Dave" Forney, Jr. is an electrical engineer who has made contributions in telecommunication system theory, specifically in coding theory and information theory....
in 1966 devised a better algorithm called generalized minimum distance (GMD) decoding which makes use of those information better. This method is achieved by measuring confidence of each received codeword, and erasing symbols whose confidence is below a desired value. And GMD decoding algorithm was one of the first examples of soft-decision decoder
Soft-decision decoder
In information theory, a soft-decision decoder is a class of algorithm used to decode data that has been encoded with an error correcting code. Whereas a hard-decision decoder operates on data that take on a fixed set of possible values , the inputs to a soft-decision decoder may take on a whole...
s. We will present three versions of the GMD decoding algorithm. The first two will be randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s while the last one will be a deterministic algorithm
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
.
Setup
- Hamming distanceHamming distanceIn information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
: Given two vectorVectorVector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
s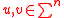
the Hamming distance between u and v, denoted by 
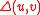, is defined to be the number of positions in which u and v differ. - Minimum distance : Let
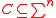be a codeCodeA code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
. The minimum distance of code C is defined to be
where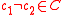 
- Code concatenation : Given
, consider two codes which we call outer code and inner code 
, and their distances are 
and 
. A concatenated code can be achieved by 
where 
. Finally we will take 
to be RS code, which has an errors and erasure decoder, and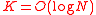 
, which in turn implies that MLD on the inner code will be poly(
) time. - Maximum likelihood decoding(MLD) : MLD is a decoding method for error correcting codes, which outputs the codeword closest to the received word in Hamming distance. The MLD function denoted by
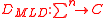is defined as follows. For every 
, 
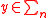. - Probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
: A probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
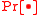on a sample space 
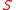is a mapping from events of 
to real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s such that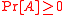
for any event 
, 
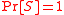, and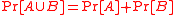 
for any two mutually exclusive events 
and 
- Expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
: The expected value of a discrete random variable
is 
.
Randomized algorithm
Consider the received word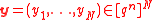 which corrupted by noisy channel. The following is the algorithm description for the general case. In this algorithm, we can decode y by just declaring an erasure at every bad position and running the errors and erasure decoding algorithm for on the resulting vector.Randomized_Decoder
Given :
.
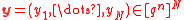- For every
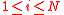, compute 
. - Set
. - For every
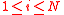, repeat : With probability 
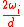, set 
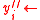?, otherwise set 
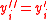. - Run errors and erasure algorithm for
on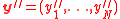 
.
Theorem 1. Let y be a received word such that there exists a codeword
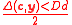such that . Then the deterministic GMD algorithm outputs .Note that a naive decoding algorithm for concatenated codes can correct up to
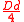errors.Lemma 1. Let the assumption in Theorem 1 hold. And if
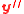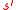has errors and erasures(when compared with ) after Step 1, then .If
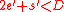, then the algorithm in Step 2 will output . The lemma above says that in expectation, this is indeed the case. Note that this is not enough to prove Theorem 1, but can be crucial in developing future variations of the algorithm.Proof of lemma 1. For every
, define 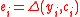. This implies thatNext for every
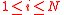, we define two indicator variables:-
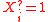iff 
and
-
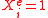iff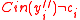 
and
We claim that we are done if we can show that for every
:
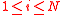Clearly, by definition
and 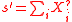. Further, by the linearityLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
of expectation, we get
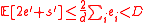. We consider two cases to prove (2) : block is correctly decoded(Case 1), block is incorrectly decoded(Case 2)Case 1:
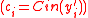
Note that if
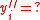then , and 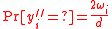implies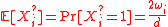, and 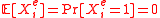.Further, by definition we have
Case 2:
In this case,
-
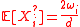and 
Since
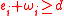, . This follows another case analysis when or not.Finally, this implies
In the following sections, we will finally show that the deterministic version of the algorithm above can do unique decoding of
up to half its design distance.Modified randomized algorithm
Note that, in the previous version of the GMD algorithm in step "3", we do not really need to use "fresh" randomnessRandomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
for each
. Now we come up with another randomized version of the GMD algorithm that uses the same randomness for every . This idea follows the algorithm below.Modified_Randomized_Decoder
Given :
, pick at random. Then every for every :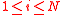
- Set
. - Compute
. - If
< 
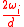, set 
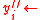?, otherwise set 
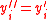. - Run errors and erasure algorithm for
on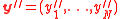 
.
For the proof of Lemma 1
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
, we only use the randomness to show that
In this version of the GMD algorithm, we note that
The second equality above follows from the choice of
. The proof of Lemma 1 can be also used to show < for version2 of GMD.In the next section, we will see how to get a deterministic version of the GMD algorithm by choosing θ from a polynomially sized set as opposed to the current infinite set
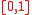.Deterministic algorithm
Let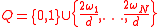. Since for each , we have
where
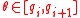for some . Note that for every , the step 1 of the second version of randomized algorithm outputs the same . Thus, we need to consider all possible value of 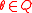. This gives the deterministic algorithm below.Deterministic_Decoder
Given :
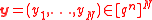, for every , repeat the following.
- Compute
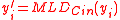for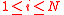 
. - Set
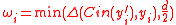for every 
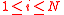. - If
< 
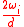, set 
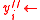?, otherwise set 
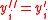. - Run errors-and-erasures algorithm for
on 
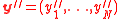. Let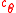 
be the codeword in 
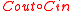corresponding to the output of the algorithm, if any. - Among all the
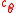output in 4, output the one closest to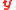 
Every loop of 1~4 can be run in polynomial time, the algorithm above can also be computed in polynomial time.
Specifically, each call to an errors and erasures decoder of
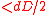errors takes 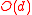time. Finally, the runtime of the algorithm above is 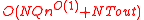where is the running time of the outer errors and erasures decoder.See also
- Concatenated codes
- Reed Solomon error correction
- Welch Berlekamp algorithmBerlekamp–Welch algorithmThe Berlekamp–Welch algorithm, also known as the Welch–Berlekamp algorithm, is named for Elwyn R. Berlekamp and Lloyd R. Welch. The algorithm efficiently corrects errors in BCH codes and Reed–Solomon codes...