Erasure code
Encyclopedia
In information theory
, an erasure code is a forward error correction
(FEC) code for the binary erasure channel
, which transforms a message of k symbols into a longer message (code word) with n symbols such that the original message can be recovered from a subset of the n symbols. The fraction r=k/n is called the code rate
, the fraction k’/k, where k’ denotes the number of symbols required for recovery, is called reception efficiency.
Optimal codes are often costly (in terms of memory usage, CPU time, or both) when n is large. Except for very simple schemes, practical solutions usually have quadratic encoding and decoding complexity
. Using FFT techniques, the complexity may be reduced to O(n log(n)); however, this is not practical.
, a check-sum is computed and appended to the k source values:
.
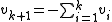The set of k+1 values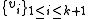
is now consistent with regard to the check-sum.
If one of these values,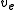
, is erased, it can be easily recovered by summing the remaining variables:
.
Alice wants to send her telephone number (555629) to Bob using err-mail. Err-mail works just like e-mail, except
Instead of asking Bob to acknowledge the messages she sends, Alice devises the following scheme.
Bob knows that the form of f(k) is
, where a and b are the two parts of the telephone number.
Now suppose Bob receives "D=777" and "E=851".
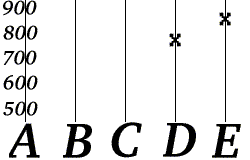
Bob can reconstruct Alice's phone number by computing the values of a and b from the values (f(4) and f(5)) he has received.
Bob can perform this procedure using any two err-mails, so the erasure code in this example has a rate of 40%.
Note that Alice cannot encode her telephone number in just one err-mail, because it contains six characters, and the maximum length of one err-mail message is five characters. If she sent her phone number in pieces, asking Bob to acknowledge receipt of each piece, at least four messages would have to be sent anyway (two from Alice, and two acknowledgments from Bob). So the erasure code in this example, which requires five messages, is quite economical.
This example is a little bit contrived. For truly generic erasure codes that work over any data set, we would need something other than the f(i) given.
. Additionally, points are now computed over a finite field
.
First we choose a finite field F with order of at least n, but usually a power of 2. The sender numbers the data symbols from 0 to k - 1 and sends them. He then constructs a (Lagrange) polynomial
p(x) of order k such that p(i) is equal to data symbol i. He then sends p(k), ..., p(n - 1). The receiver can now also use polynomial interpolation to recover the lost packets, provided he receives k symbol successfully. If the order of F is less than 2^b, where b is the number of bits in a symbol, then multiple polynomials can be used.
The sender can construct symbols k to n-1 'on the fly', i.e., distribute the workload evenly between transmission of the symbols. If the receiver wants to do his calculations 'on the fly', he can construct a new polynomial q, such that q(i) = p(i) if symbol i < k was received successfully and q(i) = 0 when symbol i < k was not received. Now let r = p - q. Firstly we know that r(i)=0 if symbol i < k has been received successfully. Secondly, if symbol i >= k has been received successfully, then r(i)=p(i) - q(i) can be calculated. So we have enough data points to construct r and evaluate it to find the lost packets. So both the sender and the receiver require O(n (n - k)) operations and only O(n - k) space for operating 'on the fly'.
using a Vandermonde matrix.
Near-optimal erasure codes trade correction capabilities for computational complexity: practical algorithms can encode and decode with linear time complexity.
Fountain code
s (also known as rateless erasure codes) are notable examples of near-optimal erasure codes. They can transform a k symbol message into a practically infinite encoded form, i.e., they can generate an arbitrary amount of redundancy symbols that can all be used for error correction. Receivers can start decoding after they have received slightly more than k encoded symbols.
Regenerating Codes address the issue of rebuilding (also called repairing) lost encoded fragments from existing encoded fragments. This issue arises in distributed
storage systems where communication to maintain encoded redundancy is a problem.
Near optimal fountain
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, an erasure code is a forward error correction
Forward error correction
In telecommunication, information theory, and coding theory, forward error correction or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels....
(FEC) code for the binary erasure channel
Binary erasure channel
A binary erasure channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter sends a bit , and the receiver either receives the bit or it receives a message that the bit was not received...
, which transforms a message of k symbols into a longer message (code word) with n symbols such that the original message can be recovered from a subset of the n symbols. The fraction r=k/n is called the code rate
Code rate
In telecommunication and information theory, the code rate of a forward error correction code is the proportion of the data-stream that is useful...
, the fraction k’/k, where k’ denotes the number of symbols required for recovery, is called reception efficiency.
Optimal erasure codes
Optimal erasure codes have the property that any k out of the n code word symbols are sufficient to recover the original message (i.e., they have optimal reception efficiency). Optimal erasure codes are maximum distance separable codes (MDS codes).Optimal codes are often costly (in terms of memory usage, CPU time, or both) when n is large. Except for very simple schemes, practical solutions usually have quadratic encoding and decoding complexity
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. Using FFT techniques, the complexity may be reduced to O(n log(n)); however, this is not practical.
Parity check
Parity check is the special case where n = k + 1. From a set of k values, a check-sum is computed and appended to the k source values: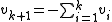. The set of k+1 values
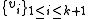is now consistent with regard to the check-sum.If one of these values,
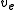, is erased, it can be easily recovered by summing the remaining variables: .Example: Err-mail (k=2)
In the simple case where k=2, redundancy symbols may be created by sampling different points along the line between the two original symbols. This is pictured with a simple example, called err-mail:Alice wants to send her telephone number (555629) to Bob using err-mail. Err-mail works just like e-mail, except
- About half of all the mail gets lost.
- Messages longer than 5 characters are illegal.
- It is very expensive (similar to air-mail).
Instead of asking Bob to acknowledge the messages she sends, Alice devises the following scheme.
- She breaks her telephone number up into two parts a=555, b=629, and sends 2 messages – "A=555" and "B=629" – to Bob.
- She constructs a linear function,
, in this case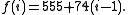 
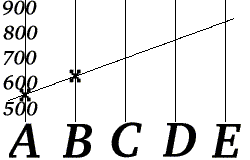
- She computes the values f(3), f(4), and f(5), and then transmits three redundant messages: "C=703", "D=777" and "E=851".
Bob knows that the form of f(k) is
, where a and b are the two parts of the telephone number.Now suppose Bob receives "D=777" and "E=851".
Bob can reconstruct Alice's phone number by computing the values of a and b from the values (f(4) and f(5)) he has received.
Bob can perform this procedure using any two err-mails, so the erasure code in this example has a rate of 40%.
Note that Alice cannot encode her telephone number in just one err-mail, because it contains six characters, and the maximum length of one err-mail message is five characters. If she sent her phone number in pieces, asking Bob to acknowledge receipt of each piece, at least four messages would have to be sent anyway (two from Alice, and two acknowledgments from Bob). So the erasure code in this example, which requires five messages, is quite economical.
This example is a little bit contrived. For truly generic erasure codes that work over any data set, we would need something other than the f(i) given.
General Case
The linear construction above can be generalized to polynomial interpolationPolynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
. Additionally, points are now computed over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
.
First we choose a finite field F with order of at least n, but usually a power of 2. The sender numbers the data symbols from 0 to k - 1 and sends them. He then constructs a (Lagrange) polynomial
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
p(x) of order k such that p(i) is equal to data symbol i. He then sends p(k), ..., p(n - 1). The receiver can now also use polynomial interpolation to recover the lost packets, provided he receives k symbol successfully. If the order of F is less than 2^b, where b is the number of bits in a symbol, then multiple polynomials can be used.
The sender can construct symbols k to n-1 'on the fly', i.e., distribute the workload evenly between transmission of the symbols. If the receiver wants to do his calculations 'on the fly', he can construct a new polynomial q, such that q(i) = p(i) if symbol i < k was received successfully and q(i) = 0 when symbol i < k was not received. Now let r = p - q. Firstly we know that r(i)=0 if symbol i < k has been received successfully. Secondly, if symbol i >= k has been received successfully, then r(i)=p(i) - q(i) can be calculated. So we have enough data points to construct r and evaluate it to find the lost packets. So both the sender and the receiver require O(n (n - k)) operations and only O(n - k) space for operating 'on the fly'.
Real world implementation
This process is implemented by Reed-Solomon codes, with code words constructed over a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
using a Vandermonde matrix.
Near-optimal erasure codes
Near-optimal erasure codes require (1+ε)k symbols to recover the message (where ε>0). Reducing ε can be done at the cost of CPU time.Near-optimal erasure codes trade correction capabilities for computational complexity: practical algorithms can encode and decode with linear time complexity.
Fountain code
Fountain code
In coding theory, fountain codes are a class of erasure codes with the property that a potentially limitless sequence of encoding symbols can be generated from a given set of source symbols such that the original source symbols can ideally be recovered from any subset of the encoding symbols of...
s (also known as rateless erasure codes) are notable examples of near-optimal erasure codes. They can transform a k symbol message into a practically infinite encoded form, i.e., they can generate an arbitrary amount of redundancy symbols that can all be used for error correction. Receivers can start decoding after they have received slightly more than k encoded symbols.
Regenerating Codes address the issue of rebuilding (also called repairing) lost encoded fragments from existing encoded fragments. This issue arises in distributed
storage systems where communication to maintain encoded redundancy is a problem.
Near optimal fountainFountain codeIn coding theory, fountain codes are a class of erasure codes with the property that a potentially limitless sequence of encoding symbols can be generated from a given set of source symbols such that the original source symbols can ideally be recovered from any subset of the encoding symbols of...
(rateless erasure) codes
- Online codesOnline codesIn computer science, online codes are an example of rateless erasure codes. These codes can encode a message into a number of symbols such that knowledge of any fraction of them allows one to recover the original message...
- LT codesLT codesIn computer science, Luby transform codes are the first class of practical fountain codes that are near optimal erasure correcting codes invented by Michael Luby in 1998 and published in 2002. Like some other fountain codes, LT codes depend on sparse bipartite graphs to trade reception overhead...
- Raptor codesRaptor codesIn computer science, raptor codes are the first known class of fountain codes with linear time encoding and decoding. They were invented by Amin Shokrollahi in 2000/2001 and were first published in 2004 as an extended abstract...
Optimal erasure codes
- Parity: used in redundant array of independent disks
- Reed-Solomon coding
- any other MDS code
- Regenerating Codes see also http://csi.usc.edu/~dimakis/StorageWiki.
External links
- Software FEC in computer communications by Luigi Rizzo describes optimal erasure correction codes
- Feclib is a near optimal extension to Luigi Rizzo's work that uses band matrices. Many parameters can be set, like the size of the width of the band and size of the finite field. It also successfully exploits the large registerProcessor registerIn computer architecture, a processor register is a small amount of storage available as part of a CPU or other digital processor. Such registers are addressed by mechanisms other than main memory and can be accessed more quickly...
size of modern CPUs. How it compares to the near optimal codes mentioned above is unknown. - Coding for Distributed Storage wiki for regenerating codes and rebuilding erasure codes.