
Community matrix
Encyclopedia
In mathematical biology
, the community matrix is the linearization
of the Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point.
The Lotka–Volterra predator-prey model is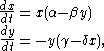
where x(t) denotes the number of predators, y(t) the number of prey, and α, β, γ and δ are constants. The linearization of these differential equations at an equilibrium point (x*, y*) has the form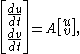
where u = x − x* and v = y − y*. The matrix A is called the community matrix. If A has an eigenvalue with positive real part then the equilibrium is unstable, but if all eigenvalues have negative real part then it is stable.
Mathematical biology
Mathematical and theoretical biology is an interdisciplinary scientific research field with a range of applications in biology, medicine and biotechnology...
, the community matrix is the linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
of the Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point.
The Lotka–Volterra predator-prey model is
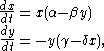
where x(t) denotes the number of predators, y(t) the number of prey, and α, β, γ and δ are constants. The linearization of these differential equations at an equilibrium point (x*, y*) has the form
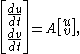
where u = x − x* and v = y − y*. The matrix A is called the community matrix. If A has an eigenvalue with positive real part then the equilibrium is unstable, but if all eigenvalues have negative real part then it is stable.

