
Gabriel's Horn
Encyclopedia
Gabriel's Horn is a geometric
figure which has infinite
surface area
but encloses a finite volume
. The name refers to the tradition identifying the Archangel Gabriel as the angel who blows the horn to announce Judgment Day, associating the divine, or infinite, with the finite. The properties of this figure were first studied by Italian
physicist and mathematician Evangelista Torricelli
.
of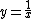 , with the domain
, with the domain
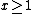 (thus avoiding the asymptote
(thus avoiding the asymptote
at x = 0) and rotating
it in three dimension
s about the x-axis. The discovery was made using Cavalieri's principle
before the invention of calculus
, but today calculus can be used to calculate the volume and surface area of the horn between x = 1 and x = a, where a > 1. Using integration (see Solid of revolution
and Surface of revolution
for details), it is possible to find the volume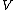 and the surface area
and the surface area 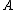 :
:

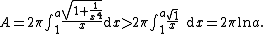
 can be as large as required, but it can be seen from the equation that the volume of the part of the horn between
can be as large as required, but it can be seen from the equation that the volume of the part of the horn between 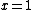 and
and  will never exceed
will never exceed  ; however, it will get closer and closer to
; however, it will get closer and closer to  as
as  becomes larger. Mathematically, the volume approaches
becomes larger. Mathematically, the volume approaches  as
as  approaches infinity. Using the limit
approaches infinity. Using the limit
notation of calculus, the volume may be expressed as:
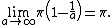
This is so because as approaches infinity,
approaches infinity, 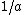 approaches zero. This means the volume approaches
approaches zero. This means the volume approaches  (1 - 0) which equals
(1 - 0) which equals  .
.
As for the area, the above shows that the area is greater than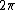 times the natural logarithm
times the natural logarithm
of . There is no upper bound
. There is no upper bound
for the natural logarithm of as it approaches infinity. That means, in this case, that the horn has an infinite surface area. That is to say;
as it approaches infinity. That means, in this case, that the horn has an infinite surface area. That is to say;
 as
as 
or
ical. However the explanation is that the bounding curve,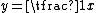 , is simply a special case–just like the simple harmonic series
, is simply a special case–just like the simple harmonic series
(Σx-1)–for which the successive area 'segments' do not decrease rapidly enough to allow for convergence to a limit. For volume segments (Σ1/x2) however, and in fact for any generally constructed higher degree curve (eg y = 1/x1.001), the same is not true and the rate of decrease in the associated series is sufficiently rapid for convergence to a (finite) limiting sum.
The apparent paradox formed part of a great dispute over the nature of infinity involving many of the key thinkers of the time including Thomas Hobbes
, John Wallis and Galileo.
The paradox can also be considered from a non-mathematical perspective. If Gabriel’s Horn existed in reality, it could be filled with a finite amount of paint since it has a finite volume. But then too, it has an infinite area; so an infinite amount of paint would therefore be required to cover its inner surface. It seems non-sensical to be able to completely fill a space with paint, yet fail to cover all that space's surface! The real-world solution to the paradox is that paint is not infinitely divisible; at some point, the throat of the Horn will become too small to allow even a single paint molecule to pass. When considering the Horn to this limited length, the practicably paintable surface of the inner surface is less than the amount of paint needed to fill it to that point.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
figure which has infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
but encloses a finite volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
. The name refers to the tradition identifying the Archangel Gabriel as the angel who blows the horn to announce Judgment Day, associating the divine, or infinite, with the finite. The properties of this figure were first studied by Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
physicist and mathematician Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
.
Mathematical definition
Gabriel's horn is formed by taking the graphGraph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of
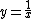 , with the domain
, with the domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
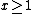 (thus avoiding the asymptote
(thus avoiding the asymptoteAsymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
at x = 0) and rotating
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
it in three dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s about the x-axis. The discovery was made using Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
before the invention of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, but today calculus can be used to calculate the volume and surface area of the horn between x = 1 and x = a, where a > 1. Using integration (see Solid of revolution
Solid of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
and Surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
for details), it is possible to find the volume
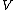 and the surface area
and the surface area 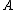 :
:
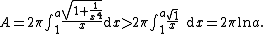
 can be as large as required, but it can be seen from the equation that the volume of the part of the horn between
can be as large as required, but it can be seen from the equation that the volume of the part of the horn between 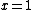 and
and  will never exceed
will never exceed  ; however, it will get closer and closer to
; however, it will get closer and closer to  as
as  becomes larger. Mathematically, the volume approaches
becomes larger. Mathematically, the volume approaches  as
as  approaches infinity. Using the limit
approaches infinity. Using the limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
notation of calculus, the volume may be expressed as:
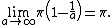
This is so because as
 approaches infinity,
approaches infinity, 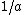 approaches zero. This means the volume approaches
approaches zero. This means the volume approaches  (1 - 0) which equals
(1 - 0) which equals  .
.As for the area, the above shows that the area is greater than
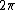 times the natural logarithm
times the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of
 . There is no upper bound
. There is no upper boundUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
for the natural logarithm of
 as it approaches infinity. That means, in this case, that the horn has an infinite surface area. That is to say;
as it approaches infinity. That means, in this case, that the horn has an infinite surface area. That is to say; as
as 
or

Apparent paradox
When the properties of Gabriel's Horn were discovered, the fact that the rotation of an infinite curve about the x-axis generates an object of finite volume was considered paradoxParadox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
ical. However the explanation is that the bounding curve,
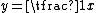 , is simply a special case–just like the simple harmonic series
, is simply a special case–just like the simple harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
(Σx-1)–for which the successive area 'segments' do not decrease rapidly enough to allow for convergence to a limit. For volume segments (Σ1/x2) however, and in fact for any generally constructed higher degree curve (eg y = 1/x1.001), the same is not true and the rate of decrease in the associated series is sufficiently rapid for convergence to a (finite) limiting sum.
The apparent paradox formed part of a great dispute over the nature of infinity involving many of the key thinkers of the time including Thomas Hobbes
Thomas Hobbes
Thomas Hobbes of Malmesbury , in some older texts Thomas Hobbs of Malmsbury, was an English philosopher, best known today for his work on political philosophy...
, John Wallis and Galileo.
The paradox can also be considered from a non-mathematical perspective. If Gabriel’s Horn existed in reality, it could be filled with a finite amount of paint since it has a finite volume. But then too, it has an infinite area; so an infinite amount of paint would therefore be required to cover its inner surface. It seems non-sensical to be able to completely fill a space with paint, yet fail to cover all that space's surface! The real-world solution to the paradox is that paint is not infinitely divisible; at some point, the throat of the Horn will become too small to allow even a single paint molecule to pass. When considering the Horn to this limited length, the practicably paintable surface of the inner surface is less than the amount of paint needed to fill it to that point.
See also
- PseudospherePseudosphereIn geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid....
- HyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
- Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
- Surface of revolutionSurface of revolutionA surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
- Zeno's paradoxesZeno's paradoxesZeno's paradoxes are a set of problems generally thought to have been devised by Greek philosopher Zeno of Elea to support Parmenides's doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion is...
External links
- Information and diagrams about Gabriel's Horn
- Torricelli's Trumpet at PlanetMath
- "Gabriel's Horn" by John Snyder, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
, 2007.

