G-test
Encyclopedia
In statistics
, G-tests are likelihood-ratio or maximum likelihood
statistical significance
tests that are increasingly being used in situations where chi-squared tests were previously recommended.
The commonly used chi-squared tests for goodness of fit to a distribution and for independence in contingency table
s are in fact approximations of the log-likelihood ratio on which the G-tests are based. This approximation was developed by Karl Pearson
because at the time it was unduly laborious to calculate log-likelihood ratios. With the advent of electronic calculators and personal computers, this is no longer a problem. G-tests are coming into increasing use, particularly since they were recommended at least since the 1981 edition of the popular statistics textbook by Sokal and Rohlf. Dunning introduced the test to the computational linguistics
community where it is now widely used.
The general formula for Pearson's chi-squared test statistic is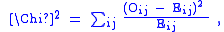
where Oi is the frequency observed in a cell, E is the frequency expected on the null hypothesis, and the sum is taken across all cells. The corresponding general formula for G is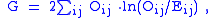
where ln denotes the natural logarithm
(log to the base e
) and the sum is again taken over all non-empty cells.
.
Let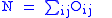
, 
, 
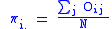and 
Then G can be expressed in several alternative forms:
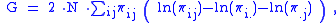
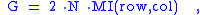
where the entropy of a discrete random variable
is defined as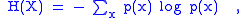
and where
is the mutual information
between the row vector and the column vector of the contingency table.
It can also be shown that the inverse document frequency weighting commonly used for text retrieval is an approximation of G applicable when the row sum for the query is much smaller than the row sum for the remainder of the corpus. Similarly, the result of Bayesian inference applied to a choice of single multinomial distribution for all rows of the contingency table taken together versus the more general alternative of a separate multinomial per row produces results very similar to the G statistic.
of G is approximately a chi-squared distribution, with the same number of degrees of freedom
as in the corresponding chi-squared test.
For samples of a reasonable size, the G-test and the chi-squared test will lead to the same conclusions. However, the approximation to the theoretical chi-squared distribution for the G-test is better than for the Pearson chi-squared tests in cases where for any cell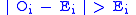
, and in any such case the G-test should always be used.
For very small samples the multinomial test
for goodness of fit, and Fisher's exact test
for contingency tables, or even Bayesian hypothesis selection are preferable to either the chi-squared test or the G-test.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, G-tests are likelihood-ratio or maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
tests that are increasingly being used in situations where chi-squared tests were previously recommended.
The commonly used chi-squared tests for goodness of fit to a distribution and for independence in contingency table
Contingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
s are in fact approximations of the log-likelihood ratio on which the G-tests are based. This approximation was developed by Karl Pearson
Karl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
because at the time it was unduly laborious to calculate log-likelihood ratios. With the advent of electronic calculators and personal computers, this is no longer a problem. G-tests are coming into increasing use, particularly since they were recommended at least since the 1981 edition of the popular statistics textbook by Sokal and Rohlf. Dunning introduced the test to the computational linguistics
Computational linguistics
Computational linguistics is an interdisciplinary field dealing with the statistical or rule-based modeling of natural language from a computational perspective....
community where it is now widely used.
The general formula for Pearson's chi-squared test statistic is
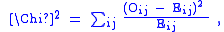
where Oi is the frequency observed in a cell, E is the frequency expected on the null hypothesis, and the sum is taken across all cells. The corresponding general formula for G is
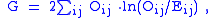
where ln denotes the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(log to the base e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
) and the sum is again taken over all non-empty cells.
Relation to mutual information
The value of G can also be expressed in terms of mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
.
Let
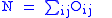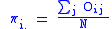, , and Then G can be expressed in several alternative forms:
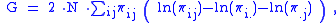
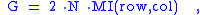
where the entropy of a discrete random variable
is defined as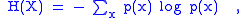and where
is the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between the row vector and the column vector of the contingency table.
It can also be shown that the inverse document frequency weighting commonly used for text retrieval is an approximation of G applicable when the row sum for the query is much smaller than the row sum for the remainder of the corpus. Similarly, the result of Bayesian inference applied to a choice of single multinomial distribution for all rows of the contingency table taken together versus the more general alternative of a separate multinomial per row produces results very similar to the G statistic.
Distribution and usage
Given the null hypothesis that the observed frequencies result from random sampling from a distribution with the given expected frequencies, the distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of G is approximately a chi-squared distribution, with the same number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
as in the corresponding chi-squared test.
For samples of a reasonable size, the G-test and the chi-squared test will lead to the same conclusions. However, the approximation to the theoretical chi-squared distribution for the G-test is better than for the Pearson chi-squared tests in cases where for any cell
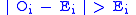, and in any such case the G-test should always be used.For very small samples the multinomial test
Multinomial test
In statistics, the multinomial test is the test of the null hypothesis that the parameters of a multinomial distribution equal specified values. It is used for categorical data; see Read and Cressie....
for goodness of fit, and Fisher's exact test
Fisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
for contingency tables, or even Bayesian hypothesis selection are preferable to either the chi-squared test or the G-test.
Application
An application of the G-test is known as the McDonald–Kreitman test in statistical genetics.Statistical software
- Software for the R programming language (homepage here) to perform the G-test is available on a Professor's software page at the University of Alberta.
- Fisher's G-Test in the GeneCycle Package of the R programming language (fisher.g.test) does not implement the G-test as described in this article, but rather Fisher's exact test of Gaussian white-noise in a time series (see Fisher, R.A. 1929 "Tests of significance in harmonic analysis").
- In SASSAS SystemSAS is an integrated system of software products provided by SAS Institute Inc. that enables programmers to perform:* retrieval, management, and mining* report writing and graphics* statistical analysis...
, one can conduct G-Test by applying the/chisqoption inproc freq.