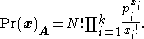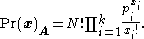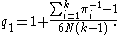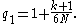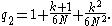Multinomial test
Encyclopedia
In statistics
, the multinomial test is the test of the null hypothesis
that the parameters of a multinomial distribution equal specified values. It is used for categorical data; see Read and Cressie.
We begin with a sample of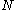
items each of which has been observed to fall into one of 
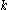categories. We can define 
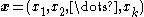as the observed numbers of items in each cell. Hence 
.
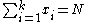Next, we define a vector of parameters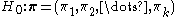
, where :
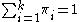. These are the parameter values under the null hypothesis
.
The exact probability of the observed configuration
under the null hypothesis is given by
The significance probability for the test is the probability of occurrence of the data set observed, or of a data set less likely than that observed, if the null hypothesis is true. Using an exact test
, this is calculated as
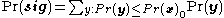
where the sum ranges over all outcomes as likely as, or less likely than, that observed. In practice this becomes computationally onerous as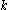
and 
increase so it is probably only worth using exact tests for small samples. For larger samples, asymptotic approximations are accurate enough and easier to calculate.
One of these approximations is the likelihood ratio. We set up an alternative hypothesis under which each value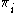
is replaced by its maximum likelihood estimate 
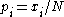. The exact probability of the observed configuration 
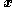under the alternative hypothesis is given by
The natural logarithm of the ratio between these two probabilities multiplied by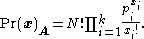
is then the statistic for the likelihood ratio test
If the null hypothesis is true, then as
increases, the distribution of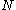 
converges to that of chi-squared
with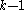
degrees of freedom. However it has long been known (e.g. Lawley 1956) that for finite sample sizes, the moments of 
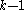are greater than those of chi-squared, thus inflating the probability of type I errors
(false positives). The difference between the moments of chi-squared and those of the test statistic are a function of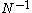
. Williams (1976) showed that the first moment can be matched as far as 
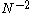if the test statistic is divided by a factor given by
In the special case where the null hypothesis is that all the values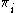
are equal to 
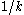(i.e. it stipulates a uniform distribution), this simplifies to
Subsequently, Smith et al. (1981) derived a dividing factor which matches the first moment as far as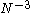
. For the case of equal values of 
, this factor is
The null hypothesis can also be tested by using Pearson's chi-squared test
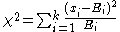
where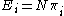
is the expected number of cases in category 
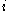under the null hypothesis. This statistic also converges to a chi-squared distribution with 
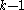degrees of freedom when the null hypothesis is true but does so from below, as it were, rather than from above as 
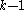does, so may be preferable to the uncorrected version of 
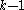for small samples.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the multinomial test is the test of the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that the parameters of a multinomial distribution equal specified values. It is used for categorical data; see Read and Cressie.
We begin with a sample of
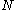items each of which has been observed to fall into one of 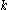categories. We can define 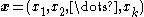as the observed numbers of items in each cell. Hence 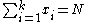.Next, we define a vector of parameters
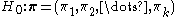, where :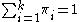. These are the parameter values under the null hypothesisNull hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
.
The exact probability of the observed configuration
under the null hypothesis is given byThe significance probability for the test is the probability of occurrence of the data set observed, or of a data set less likely than that observed, if the null hypothesis is true. Using an exact test
Exact test
In statistics, an exact test is a test where all assumptions upon which the derivation of the distribution of the test statistic is based are met, as opposed to an approximate test, in which the approximation may be made as close as desired by making the sample size big enough...
, this is calculated as
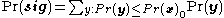
where the sum ranges over all outcomes as likely as, or less likely than, that observed. In practice this becomes computationally onerous as
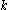and increase so it is probably only worth using exact tests for small samples. For larger samples, asymptotic approximations are accurate enough and easier to calculate.One of these approximations is the likelihood ratio. We set up an alternative hypothesis under which each value
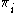is replaced by its maximum likelihood estimate 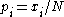. The exact probability of the observed configuration 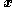under the alternative hypothesis is given by
The natural logarithm of the ratio between these two probabilities multiplied by
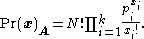is then the statistic for the likelihood ratio test
If the null hypothesis is true, then as
increases, the distribution of 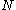converges to that of chi-squaredChi-squared
In statistics, the term chi-squared has different uses:*chi-squared distribution, a continuous probability distribution;*chi-squared statistic, a statistic used in some statistical tests;...
with
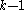degrees of freedom. However it has long been known (e.g. Lawley 1956) that for finite sample sizes, the moments of 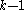are greater than those of chi-squared, thus inflating the probability of type I errorsType I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
(false positives). The difference between the moments of chi-squared and those of the test statistic are a function of
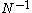. Williams (1976) showed that the first moment can be matched as far as 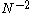if the test statistic is divided by a factor given by
In the special case where the null hypothesis is that all the values
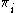are equal to 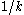(i.e. it stipulates a uniform distribution), this simplifies to
Subsequently, Smith et al. (1981) derived a dividing factor which matches the first moment as far as
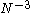. For the case of equal values of , this factor is
The null hypothesis can also be tested by using Pearson's chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
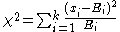
where
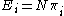is the expected number of cases in category 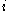under the null hypothesis. This statistic also converges to a chi-squared distribution with 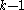degrees of freedom when the null hypothesis is true but does so from below, as it were, rather than from above as 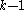does, so may be preferable to the uncorrected version of 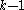for small samples.