
Functional renormalization group
Encyclopedia
In theoretical physics
, functional renormalization group (FRG) is an implementation of the renormalization group
(RG) concept which is used in quantum and statistical field theory, especially when dealing with strongly interacting systems. The method combines functional methods of quantum field theory
with the intuitive renormalization group idea of Kenneth G. Wilson
. This technique allows to interpolate smoothly between the known microscopic laws and the complicated macroscopic phenomena in physical systems. In this sense, it bridges the transition from simplicity of microphysics to complexity of macrophysics. Figuratively speaking, FRG acts as a microscope with a variable resolution. One starts with a high-resolution picture of the known microphysical laws and subsequently decreases the resolution to obtain a coarse-grained picture of macroscopic collective phenomena. The method is nonperturbative, meaning that is does not rely on an expansion in a small coupling constant
. Mathematically, FRG is based on an exact functional differential equation for a scale-dependent effective action
.
, the effective action
 is an analogue of the classical action functional
is an analogue of the classical action functional 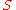 and depends on the fields of a given theory. It includes all quantum and thermal fluctuations. Variation of
and depends on the fields of a given theory. It includes all quantum and thermal fluctuations. Variation of  yields exact quantum field equations, for example for cosmology
yields exact quantum field equations, for example for cosmology
or the electrodynamics of superconductors. Mathematically, is the generating functional of the one-particle irreducible Feynman diagram
is the generating functional of the one-particle irreducible Feynman diagram
s. Interesting physics, as propagators and effective couplings for interactions, can be straightforwardly extracted from it. In a generic interacting field theory the effective action , however, is difficult to obtain. FRG provides a practical tool to calculate
, however, is difficult to obtain. FRG provides a practical tool to calculate  employing the renormalization group
employing the renormalization group
concept.
The central object in FRG is a scale-dependent effective action functional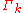 often called average action or flowing action. The dependence on the RG sliding scale
often called average action or flowing action. The dependence on the RG sliding scale 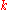 is introduced by adding a regulator
is introduced by adding a regulator
(infrared cutoff)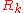 to the full inverse propagator
to the full inverse propagator 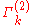 . Roughly speaking, the regulator
. Roughly speaking, the regulator  decouples slow modes with momenta
decouples slow modes with momenta 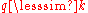 by giving them a large mass, while high momentum modes are not affected. Thus,
by giving them a large mass, while high momentum modes are not affected. Thus, 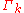 includes all quantum and statistical fluctuations with momenta
includes all quantum and statistical fluctuations with momenta  . The flowing action
. The flowing action 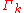 obeys the exact functional flow equation
obeys the exact functional flow equation
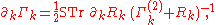
derived by Christof Wetterich
in 1993. Here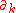 denotes a derivative with respect to the RG scale
denotes a derivative with respect to the RG scale 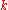 at fixed values of the fields.
at fixed values of the fields.
The functional differential equation for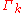 must be supplemented with the initial condition
must be supplemented with the initial condition  , where the "classical action"
, where the "classical action"  describes the physics at the microscopic ultraviolet scale
describes the physics at the microscopic ultraviolet scale 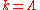 . Importantly, in the infrared limit
. Importantly, in the infrared limit  the full effective action
the full effective action
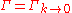 is obtained. In the Wetterich equation
is obtained. In the Wetterich equation  denotes a supertrace which sums over momenta, frequencies, internal indices, and fields (taking bosons with a plus and fermions with a minus sign). The exact flow equation for
denotes a supertrace which sums over momenta, frequencies, internal indices, and fields (taking bosons with a plus and fermions with a minus sign). The exact flow equation for 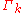 has a one-loop structure. This is an important simplification compared to perturbation theory
has a one-loop structure. This is an important simplification compared to perturbation theory
, where multi-loop diagrams must be included. The second functional derivative is the full inverse field propagator modified by the presence of the regulator
is the full inverse field propagator modified by the presence of the regulator  .
.
The renormalization group evolution of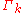 can be illustrated in the theory space, which is a multi-dimensional space of all possible running couplings
can be illustrated in the theory space, which is a multi-dimensional space of all possible running couplings 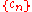 allowed by the symmetries of the problem. As schematically shown in the figure, at the microscopic ultraviolet scale
allowed by the symmetries of the problem. As schematically shown in the figure, at the microscopic ultraviolet scale 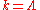 one starts with the initial condition
one starts with the initial condition  .
.
As the sliding scale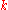 is lowered, the flowing action
is lowered, the flowing action  evolves in the theory space according to the functional flow equation. The choice of the regulator
evolves in the theory space according to the functional flow equation. The choice of the regulator 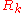 is not unique, which introduces some scheme dependence into the renormalization group
is not unique, which introduces some scheme dependence into the renormalization group
flow. For this reason, different choices of the regulator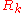 correspond to the different paths in the figure. At the infrared scale
correspond to the different paths in the figure. At the infrared scale  , however, the full effective action
, however, the full effective action 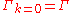 is recovered for every choice of the cut-off
is recovered for every choice of the cut-off 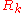 , and all trajectories meet at the same point in the theory space.
, and all trajectories meet at the same point in the theory space.
In most cases of interest the Wetterich equation can only be solved approximately. Usually some type of expansion of is performed, which is then truncated at finite order leading to a finite system of ordinary differential equations. Different systematic expansion schemes (such as the derivative expansion, vertex expansion, etc.) were developed. The choice of the suitable scheme should be physically motivated and depends on a given problem. The expansions do not necessarily involve a small parameter (like an interaction coupling constant
is performed, which is then truncated at finite order leading to a finite system of ordinary differential equations. Different systematic expansion schemes (such as the derivative expansion, vertex expansion, etc.) were developed. The choice of the suitable scheme should be physically motivated and depends on a given problem. The expansions do not necessarily involve a small parameter (like an interaction coupling constant
) and thus they are, in general, of nonperturbative nature.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, functional renormalization group (FRG) is an implementation of the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
(RG) concept which is used in quantum and statistical field theory, especially when dealing with strongly interacting systems. The method combines functional methods of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
with the intuitive renormalization group idea of Kenneth G. Wilson
Kenneth G. Wilson
Kenneth Geddes Wilson is an American theoretical physicist and Nobel Prize winner.As an undergraduate at Harvard, he was a Putnam Fellow. He earned his PhD from Caltech in 1961, studying under Murray Gell-Mann....
. This technique allows to interpolate smoothly between the known microscopic laws and the complicated macroscopic phenomena in physical systems. In this sense, it bridges the transition from simplicity of microphysics to complexity of macrophysics. Figuratively speaking, FRG acts as a microscope with a variable resolution. One starts with a high-resolution picture of the known microphysical laws and subsequently decreases the resolution to obtain a coarse-grained picture of macroscopic collective phenomena. The method is nonperturbative, meaning that is does not rely on an expansion in a small coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
. Mathematically, FRG is based on an exact functional differential equation for a scale-dependent effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
.
The flow equation
In quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
 is an analogue of the classical action functional
is an analogue of the classical action functional 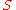 and depends on the fields of a given theory. It includes all quantum and thermal fluctuations. Variation of
and depends on the fields of a given theory. It includes all quantum and thermal fluctuations. Variation of  yields exact quantum field equations, for example for cosmology
yields exact quantum field equations, for example for cosmologyCosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
or the electrodynamics of superconductors. Mathematically,
 is the generating functional of the one-particle irreducible Feynman diagram
is the generating functional of the one-particle irreducible Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s. Interesting physics, as propagators and effective couplings for interactions, can be straightforwardly extracted from it. In a generic interacting field theory the effective action
 , however, is difficult to obtain. FRG provides a practical tool to calculate
, however, is difficult to obtain. FRG provides a practical tool to calculate  employing the renormalization group
employing the renormalization groupRenormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
concept.
The central object in FRG is a scale-dependent effective action functional
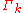 often called average action or flowing action. The dependence on the RG sliding scale
often called average action or flowing action. The dependence on the RG sliding scale 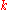 is introduced by adding a regulator
is introduced by adding a regulatorRegularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
(infrared cutoff)
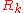 to the full inverse propagator
to the full inverse propagator 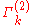 . Roughly speaking, the regulator
. Roughly speaking, the regulator  decouples slow modes with momenta
decouples slow modes with momenta 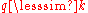 by giving them a large mass, while high momentum modes are not affected. Thus,
by giving them a large mass, while high momentum modes are not affected. Thus, 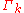 includes all quantum and statistical fluctuations with momenta
includes all quantum and statistical fluctuations with momenta  . The flowing action
. The flowing action 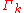 obeys the exact functional flow equation
obeys the exact functional flow equation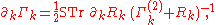
derived by Christof Wetterich
Christof Wetterich
Christof Wetterich is a German theoretical physicist. Born 1952 in Freiburg , he studied physics in Paris, Cologne and Freiburg,where he received his PhD in 1979. He worked at CERN in Geneva and DESY in Hamburg. Since 1992 he has a chair for theoreticalphysics at Ruprecht-Karls-Universität Heidelberg...
in 1993. Here
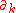 denotes a derivative with respect to the RG scale
denotes a derivative with respect to the RG scale 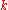 at fixed values of the fields.
at fixed values of the fields.The functional differential equation for
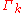 must be supplemented with the initial condition
must be supplemented with the initial condition  , where the "classical action"
, where the "classical action"  describes the physics at the microscopic ultraviolet scale
describes the physics at the microscopic ultraviolet scale 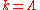 . Importantly, in the infrared limit
. Importantly, in the infrared limit  the full effective action
the full effective actionEffective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
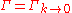 is obtained. In the Wetterich equation
is obtained. In the Wetterich equation  denotes a supertrace which sums over momenta, frequencies, internal indices, and fields (taking bosons with a plus and fermions with a minus sign). The exact flow equation for
denotes a supertrace which sums over momenta, frequencies, internal indices, and fields (taking bosons with a plus and fermions with a minus sign). The exact flow equation for 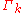 has a one-loop structure. This is an important simplification compared to perturbation theory
has a one-loop structure. This is an important simplification compared to perturbation theoryPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, where multi-loop diagrams must be included. The second functional derivative
 is the full inverse field propagator modified by the presence of the regulator
is the full inverse field propagator modified by the presence of the regulator  .
.The renormalization group evolution of
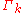 can be illustrated in the theory space, which is a multi-dimensional space of all possible running couplings
can be illustrated in the theory space, which is a multi-dimensional space of all possible running couplings 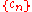 allowed by the symmetries of the problem. As schematically shown in the figure, at the microscopic ultraviolet scale
allowed by the symmetries of the problem. As schematically shown in the figure, at the microscopic ultraviolet scale 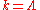 one starts with the initial condition
one starts with the initial condition  .
.As the sliding scale
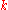 is lowered, the flowing action
is lowered, the flowing action  evolves in the theory space according to the functional flow equation. The choice of the regulator
evolves in the theory space according to the functional flow equation. The choice of the regulator 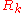 is not unique, which introduces some scheme dependence into the renormalization group
is not unique, which introduces some scheme dependence into the renormalization groupRenormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
flow. For this reason, different choices of the regulator
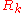 correspond to the different paths in the figure. At the infrared scale
correspond to the different paths in the figure. At the infrared scale  , however, the full effective action
, however, the full effective action 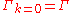 is recovered for every choice of the cut-off
is recovered for every choice of the cut-off 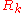 , and all trajectories meet at the same point in the theory space.
, and all trajectories meet at the same point in the theory space.In most cases of interest the Wetterich equation can only be solved approximately. Usually some type of expansion of
 is performed, which is then truncated at finite order leading to a finite system of ordinary differential equations. Different systematic expansion schemes (such as the derivative expansion, vertex expansion, etc.) were developed. The choice of the suitable scheme should be physically motivated and depends on a given problem. The expansions do not necessarily involve a small parameter (like an interaction coupling constant
is performed, which is then truncated at finite order leading to a finite system of ordinary differential equations. Different systematic expansion schemes (such as the derivative expansion, vertex expansion, etc.) were developed. The choice of the suitable scheme should be physically motivated and depends on a given problem. The expansions do not necessarily involve a small parameter (like an interaction coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
) and thus they are, in general, of nonperturbative nature.
Aspects of functional renormalization
- The Wetterich flow equation is an exact equation. However, in practice, the functional differential equation must be truncated, i.e. it must be projected to functions of a few variables or even onto some finite-dimensional sub-theory space. As in every nonperturbative method, the question of error estimate is nontrivial in functional renormalization. One way to estimate the error in FRG is to improve the truncation in successive steps, i.e. to enlarge the sub-theory space by including more and more running couplings. The difference in the flows for different truncations gives a good estimate of the error. Alternatively, one can use different regulator functions
 in a given (fixed) truncation and determine the difference of the RG flows in the infrared for the respective regulator choices. If bosonization is used, one can check the insensitivity of final results with respect to different bosonization procedures.
in a given (fixed) truncation and determine the difference of the RG flows in the infrared for the respective regulator choices. If bosonization is used, one can check the insensitivity of final results with respect to different bosonization procedures.
- In FRG, as in all RG methods, a lot of insight about a physical system can be gained from the topology of RG flows. Specifically, identification of fixed pointsFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of the renormalization group evolution is of great importance. Near fixed points the flow of running couplings effectively stops and RG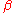 -functions approach zero. The presence of (partially) stable infrared fixed points is closely connected to the concept of universalityUniversalityUniversality may refer to:* Universality in physical science * Universality * Universality , meaning present in all places and all times* Universality...
-functions approach zero. The presence of (partially) stable infrared fixed points is closely connected to the concept of universalityUniversalityUniversality may refer to:* Universality in physical science * Universality * Universality , meaning present in all places and all times* Universality...
. Universality manifests itself in the observation that some very distinct physical systems have the same critical behavior. For instance, to good accuracy, critical exponents of the liquid-gas phase transition in water and the ferromagnetic phase transition in magnets are the same. In the renormalization group language, different systems from the same universality class flow to the same (partially) stable infrared fixed point. In this way macrophysics becomes independent of the microscopic details of the particular physical model.
- Compared to the perturbation theoryPerturbation theoryPerturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, functional renormalization does not make a strict distinction between renormalizable and nonrenormalizable couplings. All running couplings that are allowed by symmetries of the problem are generated during the FRG flow. However, the nonrenormalizable couplings approach partial fixed points very quickly during the evolution towards the infrared, and thus the flow effectively collapses on a hypersurface of the dimension given by the number of renormalizable couplings. Taking the nonrenormalizable couplings into account allows to study nonuniversal features that are sensitive to the concrete choice of the microscopic action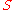 and the finite ultraviolet cutoff
and the finite ultraviolet cutoff  .
.
- The Wetterich equation can be obtained from the Legendre transformationLegendre transformationIn mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of the Polchinski functional equation, derived by Joseph Polchinski in 1984. The concept of the effective average action, used in FRG, is, however, more intuitive than the flowing bare action in the Polchinski equation. In addition, the FRG method proved to be more suitable for practical calculations.
- Typically, low-energy physics of strongly interacting systems is described by macroscopic degrees of freedom (i.e. particle excitations) which are very different from microscopic high-energy degrees of freedom. For instance, quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
is a field theory of interacting quarks and gluons. At low energies, however, proper degrees of freedom are baryons and mesons. Another example is the BEC/BCS crossover problem in condensed matter physicsCondensed matter physicsCondensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
. While the microscopic theory is defined in terms of two-component nonrelativistic fermions, at low energies a composite (particle-particle) dimer becomes an additional degree of freedom, and it is advisable to include it explicitly in the model. The low-energy composite degrees of freedom can be introduced in the description by the method of partial bosonization (Hubbard-Stratonovich transformationHubbard-Stratonovich transformationThe Hubbard–Stratonovich transformation is an exact mathematical transformation invented by Russian physicist Ruslan L. Stratonovich and popularized by British physicist John Hubbard...
). This transformation, however, is done once and for all at the UV scale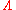 . In FRG a more efficient way to incorporate macroscopic degrees of freedom was introduced, which is known as flowing bosonization or rebosonization. With the help of a scale-dependent field transformation, this allows to perform the Hubbard-Stratonovich transformationHubbard-Stratonovich transformationThe Hubbard–Stratonovich transformation is an exact mathematical transformation invented by Russian physicist Ruslan L. Stratonovich and popularized by British physicist John Hubbard...
. In FRG a more efficient way to incorporate macroscopic degrees of freedom was introduced, which is known as flowing bosonization or rebosonization. With the help of a scale-dependent field transformation, this allows to perform the Hubbard-Stratonovich transformationHubbard-Stratonovich transformationThe Hubbard–Stratonovich transformation is an exact mathematical transformation invented by Russian physicist Ruslan L. Stratonovich and popularized by British physicist John Hubbard...
continuously at all RG scales .
.
Applications
The method was applied to numerous problems in physics, e.g.:- In statistical field theoryStatistical field theoryA statistical field theory is any model in statistical mechanics where the degrees of freedom comprise a field or fields. In other words, the microstates of the system are expressed through field configurations...
, FRG provided a unified picture of phase transitions in classical linear -symmetric scalar theories in different dimensions
-symmetric scalar theories in different dimensions 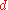 , including critical exponents for
, including critical exponents for  and the Berezinskii-Kosterlitz-Thouless phase transition for
and the Berezinskii-Kosterlitz-Thouless phase transition for  ,
,  .
.
- In gauge quantum field theory, FRG was used, for instance, to investigate the chiral phase transition and infrared properties of QCD and its large-flavor extensions.
- In condensed matter physicsCondensed matter physicsCondensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, the method proved to be successful to treat lattice models (e.g. the Hubbard modelHubbard modelThe Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
or frustrated magnetic systems), repulsive Bose gas, BEC/BCS crossover for two-component Fermi gas, Kondo effectKondo effectIn physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities. It is a measure of how electrical resistivity changes with temperature....
, disordered systems and nonequlibrium phenomena.
- Application of FRG to gravity provided solid arguments in favor of nonperturbative renormalizability of quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
in four spacetime dimensions, known as the asymptotic safety scenario.
- In mathematical physics FRG was used to prove renormalizability of different field theories.
See also
- Renormalization groupRenormalization groupIn theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
- RenormalizationRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
- Critical phenomenaCritical phenomenaIn physics, critical phenomena is the collective name associated with thephysics of critical points. Most of them stem from the divergence of thecorrelation length, but also the dynamics slows down...
- Scale invarianceScale invarianceIn physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...

