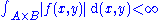Fubini's theorem
Encyclopedia
In mathematical analysis
Fubini's theorem, named after Guido Fubini
, is a result which gives conditions under which it is possible to compute a double integral using iterated integral
s. As a consequence it allows the order of integration
to be changed in iterated integrals.
. Suppose f(x,y) is A × B measurable
. If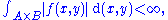
where the integral is taken with respect to a product measure
on the space over A × B, then
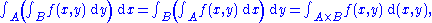
the first two integrals being iterated integrals with respect to two measures, respectively, and the third being an integral with respect to a product of these two measures.
If the above integral of the absolute value is not finite, then the two iterated integrals may actually have different values. See below for an illustration of this possibility.
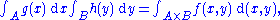
the integral on the right side being with respect to a product measure.
then
and
In this version the condition that the measures are σ-finite is necessary.
) is a successor of Fubini's theorem. The conclusion of Tonelli's theorem is identical to that of Fubini's theorem, but the assumptions are different. Tonelli's theorem states that on the product of two σ-finite measure spaces
, a product measure integral can be evaluated by way of an iterated integral for nonnegative measurable functions, regardless of whether they have finite integral.
In fact, the existence of the first integral above (the integral of the absolute value), can be guaranteed by Tonelli's theorem (see below).
A formal statement of Tonelli's theorem is identical to that of Fubini's theorem, except that the requirements are now that (X, A, μ) and (Y, B, ν) are σ-finite measure spaces, while f maps X×Y to [0, ∞].
and Stanisław Ulam, called also Fubini theorem for category, is a similar result for arbitrary second countable Baire space
s.
Let X and Y be second countable Baire space
s (or, in particular, Polish space
s), and
. Then the following are equivalent if A has the Baire property:
Even if A does not have the Baire property, 2. follows from 1.
Note that the theorem still holds (perhaps vacuously) for X - arbitrary Hausdorff space and Y - Hausdorff with countable π-base.
The theorem is analogous to regular Fubini theorem for the case where the considered function is a characteristic function of a set in a product space, with usual correspondences – meagre set with set of measure zero, comeagre set with one of full measure, a set with Baire property with a measurable set.
which is the basis for much of probability theory:
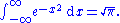
To see how Fubini's theorem is used to prove this, see Gaussian integral
.
value is finite, then the order of integration does not matter;
if we integrate first with respect to x and then with respect
to y, we get the same result as if we integrate first with
respect to y and then with respect to x. The assumption
that the integral of the absolute value is finite is
"Lebesgue integrability".
The iterated integral
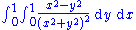
does not converge absolutely
(i.e. the integral of the
absolute value
is not finite):
That the assumption of Lebesgue integrability in Fubini's theorem
cannot be dropped can be seen by examining this particular
iterated integral. Putting "dx dy" in place
of "dy dx" has the effect of multiplying the value of
the integral by −1 because of the antisymmetry
of the
function being integrated. Therefore, unless the value of the
integral is zero, putting "dx dy" in place of
"dy dx" actually changes the value of the integral.
That is indeed what happens in this case.
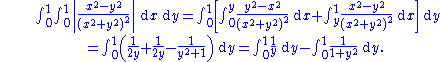
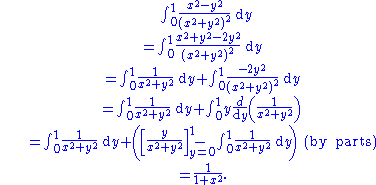
This takes care of the "inside" integral with respect to y;
now we do the "outside" integral with respect to x:
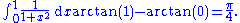
Thus we have
and
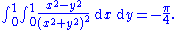
Fubini's theorem implies that since these two iterated integrals differ, the integral of the absolute value must be ∞.
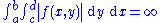
then the two iterated integrals
may have different finite values.
. Martin's axiom
implies that there exists a function on the unit square whose iterated integrals are not equal, while a variant of Freiling's axiom of symmetry
implies that in fact a strong Fubini-type theorem for [0, 1] does hold, and whenever the two iterated integrals exist they are equal. See List of statements undecidable in ZFC.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
Fubini's theorem, named after Guido Fubini
Guido Fubini
Guido Fubini was an Italian mathematician, known for Fubini's theorem and the Fubini–Study metric.Born in Venice, he was steered towards mathematics at an early age by his teachers and his father, who was himself a teacher of mathematics...
, is a result which gives conditions under which it is possible to compute a double integral using iterated integral
Iterated integral
In calculus an iterated integral is the result of applying integrals to a function of more than one variable in a way that each of the integrals considers some of the variables as given constants. For example, the function f, if y is considered a given parameter can be integrated with respect to...
s. As a consequence it allows the order of integration
Order of integration (calculus)
In calculus, interchange of the order of integration is a methodology that transforms iterated integrals of functions into other, hopefully simpler, integrals by changing the order in which the integrations are performed...
to be changed in iterated integrals.
Theorem statement
Suppose A and B are complete measure spacesMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
. Suppose f(x,y) is A × B measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
. If
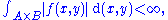
where the integral is taken with respect to a product measure
Product measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
on the space over A × B, then
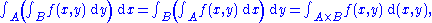
the first two integrals being iterated integrals with respect to two measures, respectively, and the third being an integral with respect to a product of these two measures.
If the above integral of the absolute value is not finite, then the two iterated integrals may actually have different values. See below for an illustration of this possibility.
Corollary
If for some functions g and h, then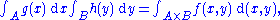the integral on the right side being with respect to a product measure.
Alternate theorem statement
Another version of Fubini's theorem states that if A and B are σ-finite measure spaces, not necessarily complete, and if either-
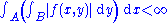or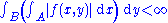 
then
and
-
.
In this version the condition that the measures are σ-finite is necessary.
Tonelli's theorem
Tonelli's theorem (named after Leonida TonelliLeonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
) is a successor of Fubini's theorem. The conclusion of Tonelli's theorem is identical to that of Fubini's theorem, but the assumptions are different. Tonelli's theorem states that on the product of two σ-finite measure spaces
Sigma-finite measure
In mathematics, a positive measure μ defined on a σ-algebra Σ of subsets of a set X is called finite if μ is a finite real number . The measure μ is called σ-finite if X is the countable union of measurable sets of finite measure...
, a product measure integral can be evaluated by way of an iterated integral for nonnegative measurable functions, regardless of whether they have finite integral.
In fact, the existence of the first integral above (the integral of the absolute value), can be guaranteed by Tonelli's theorem (see below).
A formal statement of Tonelli's theorem is identical to that of Fubini's theorem, except that the requirements are now that (X, A, μ) and (Y, B, ν) are σ-finite measure spaces, while f maps X×Y to [0, ∞].
Kuratowski-Ulam theorem
The Kuratowski-Ulam theorem, named after Polish mathematicians Kazimierz KuratowskiKazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
and Stanisław Ulam, called also Fubini theorem for category, is a similar result for arbitrary second countable Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
s.
Let X and Y be second countable Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
s (or, in particular, Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
s), and
. Then the following are equivalent if A has the Baire property:
- A is meager (respectively comeager)
- The set
is comeagre in X, where 
, where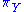 
is the projection onto Y.
Even if A does not have the Baire property, 2. follows from 1.
Note that the theorem still holds (perhaps vacuously) for X - arbitrary Hausdorff space and Y - Hausdorff with countable π-base.
The theorem is analogous to regular Fubini theorem for the case where the considered function is a characteristic function of a set in a product space, with usual correspondences – meagre set with set of measure zero, comeagre set with one of full measure, a set with Baire property with a measurable set.
Gaussian integral
One application of Fubini's theorem is the evaluation of the Gaussian integralGaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
which is the basis for much of probability theory:
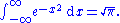
To see how Fubini's theorem is used to prove this, see Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
.
Rearranging a conditionally convergent iterated integral
Fubini's theorem tells us that if the integral of the absolutevalue is finite, then the order of integration does not matter;
if we integrate first with respect to x and then with respect
to y, we get the same result as if we integrate first with
respect to y and then with respect to x. The assumption
that the integral of the absolute value is finite is
"Lebesgue integrability".
The iterated integral
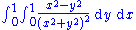
does not converge absolutely
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
(i.e. the integral of the
absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
is not finite):
That the assumption of Lebesgue integrability in Fubini's theorem
cannot be dropped can be seen by examining this particular
iterated integral. Putting "dx dy" in place
of "dy dx" has the effect of multiplying the value of
the integral by −1 because of the antisymmetry
Antisymmetry
In linguistics, antisymmetry is a theory of syntactic linearization presented in Richard Kayne's 1994 monograph The Antisymmetry of Syntax. The crux of this theory is that hierarchical structure in natural language maps universally onto a particular surface linearization, namely...
of the
function being integrated. Therefore, unless the value of the
integral is zero, putting "dx dy" in place of
"dy dx" actually changes the value of the integral.
That is indeed what happens in this case.
Proof
One way to do this without using Fubini's theorem is as follows: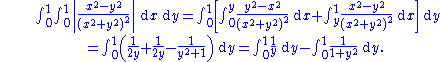Evaluation
Firstly, we consider the "inside" integral.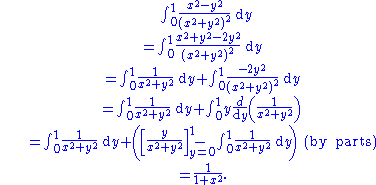This takes care of the "inside" integral with respect to y;
now we do the "outside" integral with respect to x:
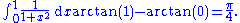
Thus we have
and
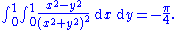
Fubini's theorem implies that since these two iterated integrals differ, the integral of the absolute value must be ∞.
Statement
When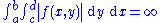then the two iterated integrals
may have different finite values.
Strong versions
The existence of strengthenings of Fubini's theorem, where the function is no longer assumed to be measurable but merely that the two iterated integrals are well defined and exist, is independent of the standard Zermelo–Fraenkel axioms of set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. Martin's axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
implies that there exists a function on the unit square whose iterated integrals are not equal, while a variant of Freiling's axiom of symmetry
Freiling's axiom of symmetry
Freiling's axiom of symmetry is a set-theoretic axiom proposed by Chris Freiling. It is based on intuition of Stuart Davidsonbut the mathematics behind it goes back to Wacław Sierpiński....
implies that in fact a strong Fubini-type theorem for [0, 1] does hold, and whenever the two iterated integrals exist they are equal. See List of statements undecidable in ZFC.
See also
- Cavalieri's principleCavalieri's principleIn geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
(a particular case of Fubini's theorem) - Coarea formulaCoarea formulaIn the mathematical field of geometric measure theory, the coarea formula expresses the integral of a function over an open set in Euclidean space in terms of the integral of the level sets of another function...