
Fréchet distance
Encyclopedia
In mathematics, the Fréchet distance is a measure of similarity between curve
s that takes into account the location and ordering of the points along the curves. It is named after Maurice Fréchet.
 be a metric space
be a metric space
. A curve
 in
in 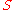 is a continuous map
is a continuous map
from the unit interval
into , i.e.,
, i.e., 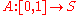 . A reparameterization
. A reparameterization
 of
of 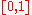 is a continuous, non-decreasing
is a continuous, non-decreasing
, surjection .
.
Let and
and  be two given curves in
be two given curves in 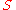 . Then, the Fréchet distance between
. Then, the Fréchet distance between  and
and  is defined as the infimum
is defined as the infimum
over all reparameterizations and
and 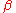 of
of  of the maximum over all
of the maximum over all  of the distance in
of the distance in  between
between 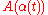 and
and 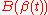 . In mathematical notation, the Fréchet distance
. In mathematical notation, the Fréchet distance 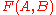 is
is
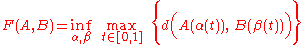
where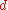 is the distance function
is the distance function
of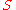 .
.
Informally, we can think of the parameter as "time". Then,
as "time". Then, 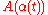 is the position of the dog and
is the position of the dog and  is the position of the dog's owner at time
is the position of the dog's owner at time  (or vice versa). The length of the leash between them at time
(or vice versa). The length of the leash between them at time  is the distance between
is the distance between 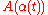 and
and 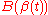 . Taking the infimum over all possible reparametrizations of
. Taking the infimum over all possible reparametrizations of 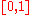 corresponds to choosing the walk along the given paths where the maximum leash length is minimized. The restriction that
corresponds to choosing the walk along the given paths where the maximum leash length is minimized. The restriction that  and
and  be non-decreasing means that neither the dog nor its owner can backtrack.
be non-decreasing means that neither the dog nor its owner can backtrack.
The Fréchet metric takes into account the flow of the two curves because the pairs of points whose distance contributes to the Fréchet distance sweep continuously along their respective curves. This makes the Fréchet distance a better measure of similarity for curves than alternatives, such as the Hausdorff distance
, for arbitrary point sets. It is possible for two curves to have small Hausdorff distance but large Fréchet distance.
The Fréchet distance and its variants find application in several problems, from morphing
and handwriting recognition
to protein structure alignment
. Alt and Godau were the first to describe a polynomial-time algorithm to compute the Fréchet distance between two polygonal curves
in Euclidean space
. The running time of their algorithm is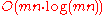 for two polygonal curves with m and n segments.
for two polygonal curves with m and n segments.
The free-space diagram between two curves for a given distance threshold ε is a two-dimensional region in the parameter space that consist of all point pairs on the two curves at distance at most ε:
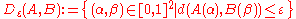
The Fréchet distance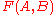 is at most ε if and only if the free-space diagram
is at most ε if and only if the free-space diagram 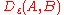 contains a path which from the lower left corner to the upper right corner which is monotone both in the horizontal and in the vertical direction.
contains a path which from the lower left corner to the upper right corner which is monotone both in the horizontal and in the vertical direction.
The discrete Fréchet distance, also called the coupling distance, is an approximation of the Fréchet metric for polygonal curves, defined by Either and Mannila. The discrete Fréchet distance considers only positions of the leash where its endpoints are located at vertices of the two polygonal curves and never in the interior of an edge. This special structure allows the discrete Fréchet distance to be computed in polynomial time by an easy dynamic programming algorithm.
When the two curves are embedded in a metric space other than Euclidean space, such as a polyhedral terrain or some Euclidean space with obstacles, the distance between two points on the curves is most naturally defined as the length of the shortest path between them. The leash is required to be a geodesic
joining its endpoints. The resulting metric between curves is called the geodesic Fréchet distance. Cook and Wenk describe a polynomial-time algorithm to compute the geodesic Fréchet distance between two polygonal curves in a simple polygon
.
If we further require that the leash must move continuously in the ambient metric space, then we obtain the notion of the homotopic Fréchet distance between two curves. The leash cannot switch discontinuously from one position to another — in particular, the leash cannot jump over obstacles, and can sweep over a mountain on a terrain only if it is long enough. The motion of the leash describes a homotopy
between the two curves. Chambers et al. describe a polynomial-time algorithm to compute the homotopic Fréchet distance between polygonal curves in the Euclidean plane with obstacles.
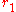 and
and 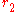 respectively is
respectively is 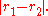
The longest leash is required when the owner stands still and the dog travels to the opposite side of the circle ( ), and the shortest leash when both owner and dog walk at a constant speed around the circle (
), and the shortest leash when both owner and dog walk at a constant speed around the circle (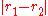 ).
).
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s that takes into account the location and ordering of the points along the curves. It is named after Maurice Fréchet.
Intuitive definition
The Fréchet distance between two curves is the minimum length of a leash required to connect a dog and its owner, constrained on two separate paths, as they walk without backtracking along their respective curves from one endpoint to the other. The definition is symmetric with respect to the two curves. Imagine a dog walking along one curve and the dog's owner walking along the other curve, connected by a leash. Both walk continuously along their respective curve from the prescribed start point to the prescribed end point of the curve. Both may vary their speed, and even stop, at arbitrary positions and for arbitrarily long. However, neither can backtrack. The Fréchet distance between the two curves is the length of the shortest leash (not the shortest leash that is sufficient for all walks, but the shortest leash of all the leashes) that is sufficient for traversing both curves in this manner.Formal definition
Let be a metric space
be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. A curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
 in
in 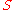 is a continuous map
is a continuous mapMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
into
 , i.e.,
, i.e., 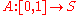 . A reparameterization
. A reparameterizationParametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
 of
of 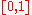 is a continuous, non-decreasing
is a continuous, non-decreasingMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
, surjection
 .
.Let
 and
and  be two given curves in
be two given curves in 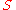 . Then, the Fréchet distance between
. Then, the Fréchet distance between  and
and  is defined as the infimum
is defined as the infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
over all reparameterizations
 and
and 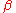 of
of 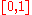 of the maximum over all
of the maximum over all  of the distance in
of the distance in  between
between 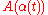 and
and 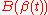 . In mathematical notation, the Fréchet distance
. In mathematical notation, the Fréchet distance 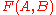 is
is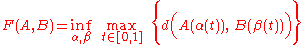
where
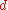 is the distance function
is the distance functionMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
of
 .
.Informally, we can think of the parameter
 as "time". Then,
as "time". Then, 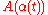 is the position of the dog and
is the position of the dog and  is the position of the dog's owner at time
is the position of the dog's owner at time  (or vice versa). The length of the leash between them at time
(or vice versa). The length of the leash between them at time  is the distance between
is the distance between 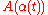 and
and 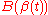 . Taking the infimum over all possible reparametrizations of
. Taking the infimum over all possible reparametrizations of 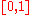 corresponds to choosing the walk along the given paths where the maximum leash length is minimized. The restriction that
corresponds to choosing the walk along the given paths where the maximum leash length is minimized. The restriction that  and
and  be non-decreasing means that neither the dog nor its owner can backtrack.
be non-decreasing means that neither the dog nor its owner can backtrack.The Fréchet metric takes into account the flow of the two curves because the pairs of points whose distance contributes to the Fréchet distance sweep continuously along their respective curves. This makes the Fréchet distance a better measure of similarity for curves than alternatives, such as the Hausdorff distance
Hausdorff distance
In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right...
, for arbitrary point sets. It is possible for two curves to have small Hausdorff distance but large Fréchet distance.
The Fréchet distance and its variants find application in several problems, from morphing
Morphing
Morphing is a special effect in motion pictures and animations that changes one image into another through a seamless transition. Most often it is used to depict one person turning into another through technological means or as part of a fantasy or surreal sequence. Traditionally such a depiction...
and handwriting recognition
Handwriting recognition
Handwriting recognition is the ability of a computer to receive and interpret intelligible handwritten input from sources such as paper documents, photographs, touch-screens and other devices. The image of the written text may be sensed "off line" from a piece of paper by optical scanning or...
to protein structure alignment
Structural alignment
Structural alignment attempts to establish homology between two or more polymer structures based on their shape and three-dimensional conformation. This process is usually applied to protein tertiary structures but can also be used for large RNA molecules...
. Alt and Godau were the first to describe a polynomial-time algorithm to compute the Fréchet distance between two polygonal curves
Polygonal chain
A polygonal chain, polygonal curve, polygonal path, or piecewise linear curve, is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points \scriptstyle called its vertices so that the curve consists of the line segments connecting the...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The running time of their algorithm is
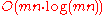 for two polygonal curves with m and n segments.
for two polygonal curves with m and n segments.The free-space diagram
An important tool for calculating the Fréchet distance of two curves is the free-space diagram, which was introduced by Alt and Godau.The free-space diagram between two curves for a given distance threshold ε is a two-dimensional region in the parameter space that consist of all point pairs on the two curves at distance at most ε:
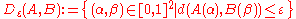
The Fréchet distance
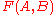 is at most ε if and only if the free-space diagram
is at most ε if and only if the free-space diagram 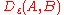 contains a path which from the lower left corner to the upper right corner which is monotone both in the horizontal and in the vertical direction.
contains a path which from the lower left corner to the upper right corner which is monotone both in the horizontal and in the vertical direction.Variants
The weak Fréchet distance is a variant of the classical Fréchet distance without the requirement that the endpoints move monotonically along their respective curves — the dog and its owner are allowed to backtrack to keep the leash between them short. Alt and Godau describe a simpler algorithm to compute the weak Fréchet distance between polygonal curves.The discrete Fréchet distance, also called the coupling distance, is an approximation of the Fréchet metric for polygonal curves, defined by Either and Mannila. The discrete Fréchet distance considers only positions of the leash where its endpoints are located at vertices of the two polygonal curves and never in the interior of an edge. This special structure allows the discrete Fréchet distance to be computed in polynomial time by an easy dynamic programming algorithm.
When the two curves are embedded in a metric space other than Euclidean space, such as a polyhedral terrain or some Euclidean space with obstacles, the distance between two points on the curves is most naturally defined as the length of the shortest path between them. The leash is required to be a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
joining its endpoints. The resulting metric between curves is called the geodesic Fréchet distance. Cook and Wenk describe a polynomial-time algorithm to compute the geodesic Fréchet distance between two polygonal curves in a simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
.
If we further require that the leash must move continuously in the ambient metric space, then we obtain the notion of the homotopic Fréchet distance between two curves. The leash cannot switch discontinuously from one position to another — in particular, the leash cannot jump over obstacles, and can sweep over a mountain on a terrain only if it is long enough. The motion of the leash describes a homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between the two curves. Chambers et al. describe a polynomial-time algorithm to compute the homotopic Fréchet distance between polygonal curves in the Euclidean plane with obstacles.
Examples
The Fréchet distance between two concentric circles of radius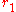 and
and 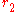 respectively is
respectively is 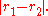
The longest leash is required when the owner stands still and the dog travels to the opposite side of the circle (
 ), and the shortest leash when both owner and dog walk at a constant speed around the circle (
), and the shortest leash when both owner and dog walk at a constant speed around the circle (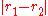 ).
).

