Friedmann-Robertson-Walker metric
Encyclopedia
The Friedmann–Lemaître–Robertson–Walker (FLRW) metric is an exact solution
of Einstein's field equations
of general relativity
; it describes a homogeneous, isotropic expanding
or contracting universe
that may be simply connected
or multiply connected. (If multiply connected, then each event in spacetime will be represented by more than one tuple of coordinates.) The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, a subset of the four scientists — Alexander Friedmann, Georges Lemaître
, Howard Percy Robertson
and Arthur Geoffrey Walker
— may be named (e.g., Friedmann–Robertson–Walker (FRW) or Robertson–Walker (RW) or Friedmann–Lemaître (FL)). This model is sometimes called the Standard Model of modern cosmology. It was developed independently by the named authors in the 1920s and 1930s.
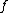
where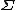
ranges over a 3-dimensional space of uniform curvature, that is, elliptical space, Euclidean space
, or hyperbolic space
. It is normally written as a function of three spatial coordinates, but there are several conventions for doing so, detailed below.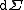
does not depend on t — all of the time dependence is in the function a(t), known as the "scale factor
".
k is a constant representing the curvature of the space. There are two common unit conventions:
A disadvantage of reduced circumference coordinates is that they cover only half of the 3-sphere in the case of positive curvature—circumferences beyond that point begin to decrease, leading to degeneracy. (This is not a problem if space is elliptical, i.e. a 3-sphere with opposite points identified.)
where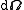
is as before and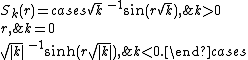
As before, k may be taken as the Gaussian curvature at a(t) = 1 or as a unitless value from the set {−1,0,+1}. Note that when k = +1, r is essentially a third angle along with θ and φ. The letter χ may be used instead of r.
Though it is usually defined piecewise as above, S is an analytic function
of both k and r. It can also be written as a power series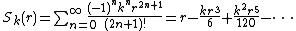
or as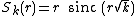
where sinc is the unnormalized sinc function and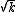
is either complex square root of k. These definitions are valid for all k.
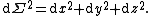
This can be extended to k ≠ 0 by defining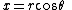
,
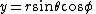, and
,
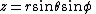where r is one of the radial coordinates defined above, but this is rare.
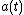does require Einstein's field equations together with a way of calculating the density, 
such as a cosmological equation of state
.
This metric has an analytic solution to Einstein's field equations
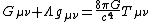giving the Friedmann equations
when the energy-momentum tensor is similarly assumed to be isotropic and homogeneous. The resulting equations are:
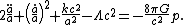
These equations are the basis of the standard big bang
cosmological model including the current ΛCDM
model. Because the FLRW model assumes homogeneity, some popular accounts mistakenly assert that the big bang model cannot account for the observed lumpiness of the universe. In a strictly FLRW model, there are no clusters of galaxies, stars or people, since these are objects much denser than a typical part of the universe. Nonetheless, the FLRW model is used as a first approximation for the evolution of the real, lumpy universe because it is simple to calculate, and models which calculate the lumpiness in the universe are added onto the FLRW models as extensions. Most cosmologists agree that the observable universe
is well approximated by an almost FLRW model, i.e., a model which follows the FLRW metric apart from primordial density fluctuations
. , the theoretical implications of the various extensions to the FLRW model appear to be well understood, and the goal is to make these consistent with observations from COBE
and WMAP.
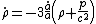
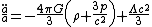
with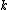
, the spatial curvature index, serving as a constant of integration for the second equation.
The first equation can be derived also from thermodynamical considerations
and is equivalent to the first law of thermodynamics
, assuming the expansion of the universe is an adiabatic process
(which is implicitly assumed in the derivation of the Friedmann–Lemaître–Robertson–Walker metric).
The second equation states that both the energy density and the pressure cause the expansion rate of the universe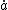
to decrease, i.e., both cause a deceleration in the expansion of the universe. This is a consequence of gravitation
, with pressure playing a similar role to that of energy (or mass) density, according to the principles of general relativity
. The cosmological constant
, on the other hand, causes an acceleration in the expansion of the universe.
term can be omitted if we make the following replacement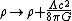
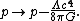
Therefore the cosmological constant
can be interpreted as arising from a form of energy which has negative pressure, equal in magnitude to its (positive) energy density:
Such form of energy—a generalization of the notion of a cosmological constant
—is known as dark energy
.
In fact, in order to get a term which causes an acceleration of the universe expansion, it is enough to have a scalar field
which satisfies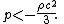
Such a field is sometimes called quintessence
.
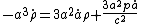
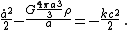
The first equation says that the decrease in the mass contained in a fixed cube (whose side is momentarily a) is the amount which leaves through the sides due to the expansion of the universe plus the mass equivalent of the work done by pressure against the material being expelled. This is the conservation of mass-energy (first law of thermodynamics
) contained within a part of the universe.
The second equation says that the kinetic energy (seen from the origin) of a particle of unit mass moving with the expansion plus its (negative) gravitational potential energy (relative to the mass contained in the sphere of matter closer to the origin) is equal to a constant related to the curvature of the universe. In other words, the energy (relative to the origin) of a co-moving particle in free-fall is conserved. General relativity merely adds a connection between the spatial curvature of the universe and the energy of such a particle: positive total energy implies negative curvature and negative total energy implies positive curvature.
The cosmological constant
term is assumed to be treated as dark energy and thus merged into the density and pressure terms.
During the Planck epoch
, one cannot neglect quantum
effects. So they may cause a deviation from the Friedmann equations.
, it remained relatively unnoticed by his contemporaries. Friedmann was in direct communication with Albert Einstein
, who, on behalf of Zeitschrift für Physik, acted as the scientific referee of Friedmann's work. Eventually Einstein acknowledged the correctness of Friedmann's calculations, but failed to appreciate the physical significance of Friedmann's predictions.
Friedmann died in 1925. In 1927, Georges Lemaître
, a Belgian astronomy student and a part-time lecturer at the University of Leuven, arrived independently at similar results as Friedmann and published them in Annals of the Scientific Society of Brussels. In the face of the observational evidence for the expansion of the universe obtained by Edwin Hubble
in the late 1920s, Lemaître's results were noticed in particular by Arthur Eddington, and in 1930–31 his paper was translated into English and published in the Monthly Notices of the Royal Astronomical Society
.
Howard Percy Robertson
from the US and Arthur Geoffrey Walker
from the UK explored the problem further during the 1930s. In 1935 Robertson and Walker rigorously proved that the FLRW metric is the only one on a spacetime that is spatially homogeneous and isotropic (as noted above, this is a geometric result and is not tied specifically to the equations of general relativity, which were always assumed by Friedmann and Lemaître).
Because the dynamics of the FLRW model were derived by Friedmann and Lemaître, the latter two names are often omitted by scientists outside the US. Conversely, US physicists often refer to it as simply "Robertson–Walker". The full four-name title is the most democratic and it is frequently used. Often the "Robertson–Walker" metric, so-called since they proved its generic properties, is distinguished from the dynamical "Friedmann-Lemaître" models, specific solutions for a(t) which assume that the only contributions to stress-energy are cold matter ("dust"), radiation, and a cosmological constant.
of space of Einstein's universe, a long-abandoned static
model that was supposed to represent our universe in idealized form. Putting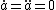
in the Friedmann equation, the radius of curvature of space of this universe (Einstein's radius) is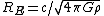
,
where
is the speed of light,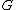 
is the Newtonian gravitational constant
, and
is the density of space of this universe. The numerical value of Einstein's radius is of the order of 1010 light years.
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of Einstein's field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
; it describes a homogeneous, isotropic expanding
Metric expansion of space
The metric expansion of space is the increase of distance between distant parts of the universe with time. It is an intrinsic expansion—that is, it is defined by the relative separation of parts of the universe and not by motion "outward" into preexisting space...
or contracting universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
that may be simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
or multiply connected. (If multiply connected, then each event in spacetime will be represented by more than one tuple of coordinates.) The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, a subset of the four scientists — Alexander Friedmann, Georges Lemaître
Georges Lemaître
Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...
, Howard Percy Robertson
Howard Percy Robertson
Howard Percy Robertson was an American mathematician and physicist known for contributions related to physical cosmology and the uncertainty principle...
and Arthur Geoffrey Walker
Arthur Geoffrey Walker
Arthur Geoffrey Walker was a leading mathematician who made important contributions to physics and physical cosmology. He was born in Watford, Hertfordshire, England....
— may be named (e.g., Friedmann–Robertson–Walker (FRW) or Robertson–Walker (RW) or Friedmann–Lemaître (FL)). This model is sometimes called the Standard Model of modern cosmology. It was developed independently by the named authors in the 1920s and 1930s.
General metric
The FLRW metric starts with the assumption of homogeneity and isotropy of space. It also assumes that the spatial component of the metric can be time-dependent. The generic metric which meets these conditions is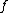where
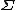ranges over a 3-dimensional space of uniform curvature, that is, elliptical space, Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, or hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. It is normally written as a function of three spatial coordinates, but there are several conventions for doing so, detailed below.
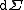does not depend on t — all of the time dependence is in the function a(t), known as the "scale factorScale factor (Universe)
The scale factor or cosmic scale factor parameter of the Friedmann equations is a function of time which represents the relative expansion of the universe. It is sometimes called the Robertson-Walker scale factor...
".
Reduced-circumference polar coordinates
In reduced-circumference polar coordinates the spatial metric has the formk is a constant representing the curvature of the space. There are two common unit conventions:
- k may be taken to have units of length−2, in which case r has units of length and a(t) is unitless. k is then the Gaussian curvatureGaussian curvatureIn differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of the space at the time when a(t) = 1. r is sometimes called the reduced circumference because it is equal to the measured circumference of a circle (at that value of r), centered at the origin, divided by 2 (like the r of Schwarzschild coordinatesSchwarzschild coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
). Where appropriate, a(t) is often chosen to equal 1 in the present cosmological era, so that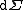
measures comoving distanceComoving distanceIn standard cosmology, comoving distance and proper distance are two closely related distance measures used by cosmologists to define distances between objects...
. - Alternatively, k may be taken to belong to the set {−1,0,+1} (for negative, zero, and positive curvature respectively). Then r is unitless and a(t) has units of length. When k = ±1, a(t) is the radius of curvatureRadius of curvature (mathematics)In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
of the space, and may also be written R(t).
A disadvantage of reduced circumference coordinates is that they cover only half of the 3-sphere in the case of positive curvature—circumferences beyond that point begin to decrease, leading to degeneracy. (This is not a problem if space is elliptical, i.e. a 3-sphere with opposite points identified.)
Hyperspherical coordinates
In hyperspherical or curvature-normalized coordinates the coordinate r is proportional to radial distance; this giveswhere
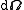is as before and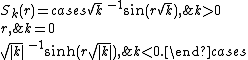As before, k may be taken as the Gaussian curvature at a(t) = 1 or as a unitless value from the set {−1,0,+1}. Note that when k = +1, r is essentially a third angle along with θ and φ. The letter χ may be used instead of r.
Though it is usually defined piecewise as above, S is an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of both k and r. It can also be written as a power series
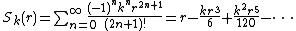
or as
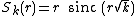
where sinc is the unnormalized sinc function and
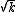is either complex square root of k. These definitions are valid for all k.Cartesian coordinates
When k = 0 one may write simply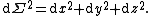This can be extended to k ≠ 0 by defining
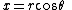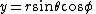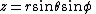,, and,where r is one of the radial coordinates defined above, but this is rare.
Solutions
Einstein's field equations are not used in deriving the general form for the metric: it follows from the geometric properties of homogeneity and isotropy. However, determining the time evolution of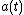 does require Einstein's field equations together with a way of calculating the density, such as a cosmological equation of stateEquation of state (cosmology)
In cosmology, the equation of state of a perfect fluid is characterized by a dimensionless number \! w, equal to the ratio of its pressure \! p to its energy density \! \rho: \! w=p/\rho...
.
This metric has an analytic solution to Einstein's field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
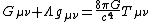giving the Friedmann equationsFriedmann equations
The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity...
when the energy-momentum tensor is similarly assumed to be isotropic and homogeneous. The resulting equations are:
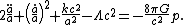
These equations are the basis of the standard big bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
cosmological model including the current ΛCDM
Lambda-CDM model
ΛCDM or Lambda-CDM is an abbreviation for Lambda-Cold Dark Matter, which is also known as the cold dark matter model with dark energy...
model. Because the FLRW model assumes homogeneity, some popular accounts mistakenly assert that the big bang model cannot account for the observed lumpiness of the universe. In a strictly FLRW model, there are no clusters of galaxies, stars or people, since these are objects much denser than a typical part of the universe. Nonetheless, the FLRW model is used as a first approximation for the evolution of the real, lumpy universe because it is simple to calculate, and models which calculate the lumpiness in the universe are added onto the FLRW models as extensions. Most cosmologists agree that the observable universe
Observable universe
In Big Bang cosmology, the observable universe consists of the galaxies and other matter that we can in principle observe from Earth in the present day, because light from those objects has had time to reach us since the beginning of the cosmological expansion...
is well approximated by an almost FLRW model, i.e., a model which follows the FLRW metric apart from primordial density fluctuations
Primordial fluctuations
Primordial fluctuations are density variations in the early universe which are considered the seeds of all structure in the universe. Currently, the most widely accepted explanation for their origin is in the context of cosmic inflation...
. , the theoretical implications of the various extensions to the FLRW model appear to be well understood, and the goal is to make these consistent with observations from COBE
COBE
The COsmic Background Explorer , also referred to as Explorer 66, was a satellite dedicated to cosmology. Its goals were to investigate the cosmic microwave background radiation of the universe and provide measurements that would help shape our understanding of the cosmos.This work provided...
and WMAP.
Interpretation
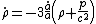
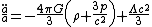
The pair of equations given above is equivalent to the following pair of equationswith
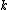, the spatial curvature index, serving as a constant of integration for the second equation.The first equation can be derived also from thermodynamical considerations
Thermodynamics of the universe
The thermodynamics of the universe is dictated by which form of energy dominates it - relativistic particles which are referred to as radiation, or non-relativistic particles which are referred to as matter...
and is equivalent to the first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
, assuming the expansion of the universe is an adiabatic process
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
(which is implicitly assumed in the derivation of the Friedmann–Lemaître–Robertson–Walker metric).
The second equation states that both the energy density and the pressure cause the expansion rate of the universe
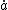to decrease, i.e., both cause a deceleration in the expansion of the universe. This is a consequence of gravitationGravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, with pressure playing a similar role to that of energy (or mass) density, according to the principles of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. The cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
, on the other hand, causes an acceleration in the expansion of the universe.
The cosmological constant term
The cosmological constantCosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
term can be omitted if we make the following replacement
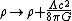
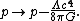
Therefore the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
can be interpreted as arising from a form of energy which has negative pressure, equal in magnitude to its (positive) energy density:
Such form of energy—a generalization of the notion of a cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
—is known as dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
.
In fact, in order to get a term which causes an acceleration of the universe expansion, it is enough to have a scalar field
Scalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
which satisfies
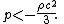
Such a field is sometimes called quintessence
Quintessence (physics)
In physics, quintessence is a hypothetical form of dark energy postulated as an explanation of observations of an accelerating universe. It has been proposed by some physicists to be a fifth fundamental force...
.
Newtonian interpretation
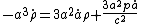
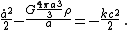
The Friedmann equations are equivalent to this pair of equations:The first equation says that the decrease in the mass contained in a fixed cube (whose side is momentarily a) is the amount which leaves through the sides due to the expansion of the universe plus the mass equivalent of the work done by pressure against the material being expelled. This is the conservation of mass-energy (first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
) contained within a part of the universe.
The second equation says that the kinetic energy (seen from the origin) of a particle of unit mass moving with the expansion plus its (negative) gravitational potential energy (relative to the mass contained in the sphere of matter closer to the origin) is equal to a constant related to the curvature of the universe. In other words, the energy (relative to the origin) of a co-moving particle in free-fall is conserved. General relativity merely adds a connection between the spatial curvature of the universe and the energy of such a particle: positive total energy implies negative curvature and negative total energy implies positive curvature.
The cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
term is assumed to be treated as dark energy and thus merged into the density and pressure terms.
During the Planck epoch
Planck epoch
In physical cosmology, the Planck epoch , named after Max Planck, is the earliest period of time in the history of the universe, from zero to approximately 10−43 seconds , during which, it is believed, quantum effects of gravity were significant...
, one cannot neglect quantum
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
effects. So they may cause a deviation from the Friedmann equations.
Name and history
The main results of the FLRW model were first derived by the Soviet mathematician Alexander Friedmann in 1922 and 1924. Although his work was published in the prestigious physics journal Zeitschrift für PhysikZeitschrift für Physik
The European Physical Journal is a joint publication of EDP Sciences, Springer Science+Business Media, and the Società Italiana di Fisica...
, it remained relatively unnoticed by his contemporaries. Friedmann was in direct communication with Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, who, on behalf of Zeitschrift für Physik, acted as the scientific referee of Friedmann's work. Eventually Einstein acknowledged the correctness of Friedmann's calculations, but failed to appreciate the physical significance of Friedmann's predictions.
Friedmann died in 1925. In 1927, Georges Lemaître
Georges Lemaître
Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...
, a Belgian astronomy student and a part-time lecturer at the University of Leuven, arrived independently at similar results as Friedmann and published them in Annals of the Scientific Society of Brussels. In the face of the observational evidence for the expansion of the universe obtained by Edwin Hubble
Edwin Hubble
Edwin Powell Hubble was an American astronomer who profoundly changed the understanding of the universe by confirming the existence of galaxies other than the Milky Way - our own galaxy...
in the late 1920s, Lemaître's results were noticed in particular by Arthur Eddington, and in 1930–31 his paper was translated into English and published in the Monthly Notices of the Royal Astronomical Society
Monthly Notices of the Royal Astronomical Society
Monthly Notices of the Royal Astronomical Society is one of the world's leading scientific journals in astronomy and astrophysics. It has been in continuous existence since 1827 and publishes peer-reviewed letters and papers reporting original research in relevant fields...
.
Howard Percy Robertson
Howard Percy Robertson
Howard Percy Robertson was an American mathematician and physicist known for contributions related to physical cosmology and the uncertainty principle...
from the US and Arthur Geoffrey Walker
Arthur Geoffrey Walker
Arthur Geoffrey Walker was a leading mathematician who made important contributions to physics and physical cosmology. He was born in Watford, Hertfordshire, England....
from the UK explored the problem further during the 1930s. In 1935 Robertson and Walker rigorously proved that the FLRW metric is the only one on a spacetime that is spatially homogeneous and isotropic (as noted above, this is a geometric result and is not tied specifically to the equations of general relativity, which were always assumed by Friedmann and Lemaître).
Because the dynamics of the FLRW model were derived by Friedmann and Lemaître, the latter two names are often omitted by scientists outside the US. Conversely, US physicists often refer to it as simply "Robertson–Walker". The full four-name title is the most democratic and it is frequently used. Often the "Robertson–Walker" metric, so-called since they proved its generic properties, is distinguished from the dynamical "Friedmann-Lemaître" models, specific solutions for a(t) which assume that the only contributions to stress-energy are cold matter ("dust"), radiation, and a cosmological constant.
Einstein's radius of the Universe
Einstein's radius of the universe is the radius of curvatureRadius of curvature (mathematics)
In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
of space of Einstein's universe, a long-abandoned static
Static spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
model that was supposed to represent our universe in idealized form. Putting
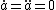
in the Friedmann equation, the radius of curvature of space of this universe (Einstein's radius) is
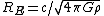,where
is the speed of light, 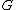is the Newtonian gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, and
is the density of space of this universe. The numerical value of Einstein's radius is of the order of 1010 light years.