The flatness problem is a cosmological

Physical cosmology

Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...

 fine-tuning

Fine-tuning

In theoretical physics, fine-tuning refers to circumstances when the parameters of a model must be adjusted very precisely in order to agree with observations. Theories requiring fine-tuning are regarded as problematic in the absence of a known mechanism to explain why the parameters happen to...

 problem within the Big Bang

Big Bang

The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...

 model of the universe. Such problems arise from the observation that some of the initial conditions of the universe appear to be fine-tuned to very 'special' values, and that a small deviation from these values would have had massive effects on the nature of the universe at the current time.

In the case of the flatness problem, the parameter which appears fine-tuned is the density of matter and energy in the universe. This value affects the curvature of space-time, with a very specific critical value being required for a flat universe. The current density of the universe is observed to be very close to this critical value. Since the total density departs rapidly from the critical value over cosmic time

Cosmic time

Cosmic time is the time coordinate commonly used in the Big Bang models of physical cosmology. It is defined for homogeneous, expanding universes as follows: Choose a time coordinate so that the universe has the same density everywhere at each moment in time Cosmic time (also known as time since...

, the early universe must have had a density even closer to the critical density, departing from it by one part in 10⁶² or less. This leads cosmologists to question how the initial density came to be so closely fine-tuned to this 'special' value.

The problem was first mentioned by Robert Dicke in 1969. The most commonly accepted solution among cosmologists is cosmic inflation

Cosmic inflation

In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...

, the idea that the universe went through a brief period of extremely rapid expansion in the first fraction of a second after the Big Bang; along with the monopole problem and the horizon problem

Horizon problem

The horizon problem is a problem with the standard cosmological model of the Big Bang which was identified in the 1970s. It points out that different regions of the universe have not "contacted" each other because of the great distances between them, but nevertheless they have the same temperature...

, the flatness problem is one of the three primary motivations for inflationary theory.

Energy density and the Friedmann equation

According to Einstein

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

's field equations

Einstein field equations

The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...

 of general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, the structure of spacetime

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

 is affected by the presence of matter

Matter

Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...

 and energy. On small scales space appears flat – as does the surface of the Earth if one looks at a small area. On large scales however, space is bent by the gravitational effect of matter. Since relativity indicates that matter and energy are equivalent, this effect is also produced by the presence of energy (such as light and other electromagnetic radiation) in addition to matter. The amount of bending (or curvature

Shape of the Universe

The shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...

) of the universe depends on the density of matter/energy present.

This relationship can be expressed by the first Friedmann equation. In a universe without a cosmological constant

Cosmological constant

In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...

, this is:


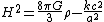
Here 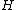is the Hubble parameter, a measure of the rate at which the universe is expanding. 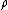is the total density of mass and energy in the universe, is the scale factor (essentially the 'size' of the universe), and is the curvature parameter — that is, a measure of how curved spacetime is. A positive, zero or negative value of corresponds to a respectively closed, flat or open universe. The constants 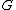and are Newton's gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

 and the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

, respectively.

Cosmologists often simplify this equation by defining a critical density, 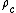. For a given value of , this is defined as the density required for a flat universe, i.e. . Thus the above equation implies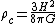
.

Since the constant 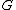is known and the expansion rate 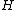can be measured by observing the speed at which distant galaxies are receding from us,
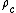can be determined. Its value is currently around . The ratio of the actual density to this critical value is called Ω, and its difference from 1 determines the geometry of the universe: corresponds to a greater than critical density, , and hence a closed universe. gives a low density open universe, and Ω equal to exactly 1 gives a flat universe.

The Friedmann equation above can now be rearranged as follows:




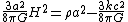
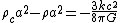
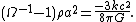
The right hand side of this expression contains only constants, and therefore the left hand side must remain constant throughout the evolution of the universe.

As the universe expands the scale factor increases, but the density 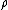decreases as matter (or energy) becomes spread out. For the standard model of the universe which contains mainly matter and radiation for most of its history, 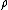decreases more quickly than 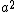increases, and so the factor will decrease. Since the time of the Planck era, shortly after the Big Bang, this term has decreased by a factor of around and so must have increased by a similar amount to retain the constant value of their product.

Current value of Ω

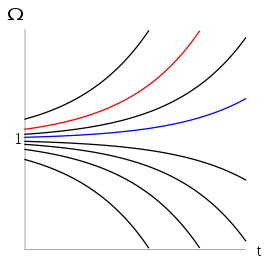
Measurement

The value of Ω at the present time is denoted Ω₀. This value can be deduced by measuring the curvature of spacetime (since Ω=1, or , is defined as the density for which the curvature k=0). The curvature can be inferred from a number of observations.

One such observation is that of anisotropies (that is, variations with direction - see below) in the Cosmic Microwave Background (CMB) radiation. The CMB is electromagnetic radiation

Electromagnetic radiation

Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...

 which fills the universe, left over from an early stage in its history when it was filled with photons and a hot, dense plasma

Plasma (physics)

In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...

. This plasma cooled as the universe expanded, and when it cooled enough to form stable atoms it no longer absorbed the photons. The photons present at that stage have been propagating ever since, growing fainter and less energetic as they spread through the ever-expanding universe.

The temperature of this radiation is almost the same at all points on the sky, but there is a slight variation (around one part in 100,000) between the temperature received from different directions. The angular scale of these fluctuations - the typical angle between a hot patch and a cold patch on the skySince there are fluctuations on many scales, not a single angular separation between hot and cold spots, the necessary measure is the angular scale of the first peak in the anisotropies' power spectrum. See Cosmic Microwave Background#Primary anisotropy. - depends on the curvature of the universe which in turn depends on its density as described above. Thus, measurements of this angular scale allow an estimation of Ω₀.

Another probe of Ω₀ is the frequency of Type-Ia

Type Ia supernova

A Type Ia supernova is a sub-category of supernovae, which in turn are a sub-category of cataclysmic variable stars, that results from the violent explosion of a white dwarf star. A white dwarf is the remnant of a star that has completed its normal life cycle and has ceased nuclear fusion...

 supernovae at different distances from Earth. These supernovae, the explosions of massive stars, are a type of standard candle; this means that the processes governing their intrinsic brightness are well understood so that a measure of apparent brightness when seen from Earth can be used to derive accurate distance measures for them (the apparent brightness decreasing in proportion to the square of the distance - see luminosity distance). Comparing this distance to the redshift

Redshift

In physics , redshift happens when light seen coming from an object is proportionally increased in wavelength, or shifted to the red end of the spectrum...

 of the supernovae gives a measure of the rate at which the universe has been expanding at different points in history. Since the expansion rate evolves differently over time in cosmologies with different total densities, Ω₀ can be inferred from the supernovae data.

Data from the Wilkinson Microwave Anisotropy Probe

Wilkinson Microwave Anisotropy Probe

The Wilkinson Microwave Anisotropy Probe — also known as the Microwave Anisotropy Probe , and Explorer 80 — is a spacecraft which measures differences in the temperature of the Big Bang's remnant radiant heat — the Cosmic Microwave Background Radiation — across the full sky. Headed by Professor...

 (measuring CMB anisotropies) combined with that from the Sloan Digital Sky Survey

Sloan Digital Sky Survey

The Sloan Digital Sky Survey or SDSS is a major multi-filter imaging and spectroscopic redshift survey using a dedicated 2.5-m wide-angle optical telescope at Apache Point Observatory in New Mexico, United States. The project was named after the Alfred P...

 and observations of type-Ia supernovae constrain Ω₀ to be 1 within 1%. In other words the term |Ω − 1| is currently less than 0.01, and therefore must have been less than 10⁻⁶² at the Planck era.

Implication

This tiny value is the crux of the flatness problem. If the initial density of the universe could take any value, it would seem extremely surprising to find it so 'finely tuned' to the critical value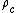 . Indeed, a very small departure of Ω from 1 in the early universe would have been magnified during billions of years of expansion to create a current density very far from critical. In the case of an overdensity this would lead to a universe so dense it would cease expanding and collapse into a Big Crunch

Big Crunch

In physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...

 (an opposite to the Big Bang in which all matter and energy falls back into an incredibly dense state) in a few years or less; in the case of an underdensity it would expand so quickly and become so sparse it would soon seem essentially empty, and gravity would not be strong enough by comparison to cause matter to collapse and form galaxies. In either case the universe would contain no complex structures such as galaxies, stars, planets and people.

This problem with the Big Bang model was first pointed out by Robert Dicke in 1969, and it motivated a search for some reason the density should take such a specific value.

Solutions to the problem

Some cosmologists agreed with Dicke that the flatness problem was a serious one, in need of a fundamental reason for the closeness of the density to criticality. But there was also a school of thought which denied that there was a problem to solve, arguing instead that since the universe must have some density it may as well have one close to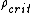 as far from it, and that speculating on a reason for any particular value was "beyond the domain of science". Enough cosmologists saw the problem as a real one, however, for various solutions to be proposed.

Anthropic principle

One solution to the problem is to invoke the anthropic principle

Anthropic principle

In astrophysics and cosmology, the anthropic principle is the philosophical argument that observations of the physical Universe must be compatible with the conscious life that observes it. Some proponents of the argument reason that it explains why the Universe has the age and the fundamental...

, which states that humans should take into account the conditions necessary for them to exist when speculating about causes of the universe's properties. If two types of universe seem equally likely but only one is suitable for the evolution of intelligent life

Intelligent Life

Intelligent life may refer to:*Intelligence including:**Animal cognition**Extraterrestrial intelligence - theoretically intelligent Extraterrestrial life...

, the anthropic principle suggests that finding ourselves in that universe is no surprise: if the other universe had existed instead, there would be no observers to notice the fact.

The principle can be applied to solve the flatness problem in two somewhat different ways. The first (an application of the 'strong anthropic principle') was suggested by C. B. Collins

C. B. Collins

C. B. Collins is a physicist and professor at the University of Texas at Dallas. He founded the Center for Quantum Electronics at that university in 1975...

 and Stephen Hawking

Stephen Hawking

Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...

, who in 1973 considered the existence of an infinite number of universes such that every possible combination of initial properties was held by some universe. In such a situation, they argued, only those universes with exactly the correct density for forming galaxies and stars would give rise to intelligent observers such as humans: therefore, the fact that we observe Ω to be so close to 1 would be "simply a reflection of our own existence."

An alternative approach, which makes use of the 'weak anthropic principle', is to suppose that the universe is infinite in size, but with the density varying in different places (i.e. an inhomogeneous

Homogeneity (physics)

In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...

 universe). Thus some regions will be over-dense and some under-dense . These regions may be extremely far apart - perhaps so far that light has not had time to travel from one to another during the age of the universe

Age of the universe

The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...

 (that is, they lie outside one another's cosmological horizons). Therefore each such region would behave essentially as a separate universe: if we happened to live in a large patch of almost-critical density we would have no way of knowing of the existence of far-off under- or over-dense patches since no light or other signal has reached us from them. An appeal to the anthropic principle can then be made, arguing that intelligent life would only arise in those patches with Ω very close to 1, and that therefore our living in such a patch is unsurprising.

This latter argument makes use of a version of the anthropic principle which is 'weaker' in the sense that it requires no speculation on multiple universes, or on the probabilities of various different universes existing instead of the current one. It requires only a single universe which is infinite - or merely large enough that many disconnected patches can form - and that the density varies in different regions (which is certainly the case on smaller scales, giving rise to galactic clusters and voids

Void (astronomy)

In astronomy, voids are the empty spaces between filaments, the largest-scale structures in the Universe, that contain very few, or no, galaxies. They were first discovered in 1978 during a pioneering study by Stephen Gregory and Laird A. Thompson at the Kitt Peak National Observatory...

).

However, the Anthropic Principle has been criticised by many scientists. For example, in 1979 Bernard Carr and Martin Rees argued that the principle “is entirely post hoc: it has not yet been used to predict any feature of the Universe.” Others have taken objection to its philosophical basis, with Ernan McMullin

Ernan McMullin

Ernan McMullin was the O’Hara Professor of Philosophy Emeritus at the University of Notre Dame. He was an internationally-respected philosopher of science who has written and lectured extensively on subjects ranging from the relationship between cosmology and theology, to the role of values in...

 writing in 1994 that "the weak Anthropic principle is trivial ... and the strong Anthropic principle is indefensible." Since many physicists and philosophers of science do not consider the principle to be compatible with the scientific method

Scientific method

Scientific method refers to a body of techniques for investigating phenomena, acquiring new knowledge, or correcting and integrating previous knowledge. To be termed scientific, a method of inquiry must be based on gathering empirical and measurable evidence subject to specific principles of...

, another explanation for the flatness problem was needed.

Inflation

The standard solution to the Flatness Problem invokes cosmic inflation, a process whereby the universe expands exponentially

Exponential growth

Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...

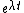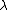 quickly (i.e. grows as with time , for some constant ) during a short period in its early history. The theory of inflation was first proposed in 1979, and published in 1981, by Alan Guth

Alan Guth

Alan Harvey Guth is an American theoretical physicist and cosmologist. Guth has researched elementary particle theory...

. His two main motivations for doing so were the flatness problem and the horizon problem, another fine-tuning problem of physical cosmology.

The proposed cause of inflation is a field

Field (physics)

In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...

 which permeates space and drives the expansion. The field contains a certain energy density, but unlike the density of the matter or radiation present in the late universe, which decrease over time, the density of the inflationary field remains roughly constant as space expands. Therefore the term 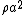increases extremely rapidly as the scale factor grows exponentially. Recalling the Friedman Equation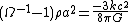
,

and the fact that the right-hand side of this expression is constant, the term 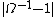must therefore decrease with time.

Thus if 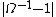initially takes any arbitrary value, a period of inflation can force it down towards 0 and leave it extremely small - around 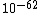as required above, for example. Subsequent evolution of the universe will cause the value to grow, bringing it to the currently observed value of around 0.01. Thus the sensitive dependence on the initial value of Ω has been removed: a large and therefore 'unsurprising' starting value need not become massively amplified and lead to a very curved universe with no opportunity to form galaxies and other structures.

This success in solving the flatness problem is considered one of the major motivations for inflationary theory.

Post inflation

Although inflationary theory is regarded as having had much success, and the evidence for it as compelling, it is not universally accepted: cosmologists recognise that there are still gaps in the theory and are open to the possibility that future observations will disprove it. In particular, in the absence of any firm evidence for what the field driving inflation should be, many different versions of the theory have been proposed. Many of these contain parameters or initial conditions which themselves require fine-tuning in much the way that the early density does without inflation.

For these reasons work is still being done on alternative solutions to the flatness problem. These have included non-standard interpretations of the effect of dark energy and gravity, particle production in an oscillating universe, and use of a Bayesian statistical

Bayesian statistics

Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...

approach to argue that the problem is non-existent. The latter argument, suggested for example by Evrard and Coles, maintains that the idea that Ω being close to 1 is 'unlikely' is based on assumptions about the likely distribution of the parameter which are not necessarily justified.

Despite this ongoing work, inflation remains by far the dominant explanation for the flatness problem.