
Fierz identity
Encyclopedia
In theoretical physics
, a Fierz identity is an identity that allows one to rewrite bilinear
s of the product of two spinor
s as a linear combination
of products of the bilinears of the individual spinors. It is named after Swiss physicist Markus Fierz
.
There is a version of the Fierz identities for Dirac spinors and there is another version for Weyl spinors. And there are versions for other dimensions besides 3+1 dimensions.
Spinor bilinears can be thought of as elements of a Clifford Algebra
. Then the Fierz identity is the concrete realization of the relation to the exterior algebra.
The identities for a generic scalar written as the contraction of two Dirac bilinears of the same type can be written with coefficients according the following table.
For example the V × V product can be expanded as,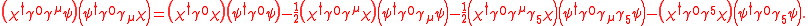
Simplifications arise when the considered spinors are chiral or Majorana spinors as some term in the expansion can be vanishing.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a Fierz identity is an identity that allows one to rewrite bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
s of the product of two spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of products of the bilinears of the individual spinors. It is named after Swiss physicist Markus Fierz
Markus Fierz
Markus Eduard Fierz was a Swiss physicist, particularly remembered for his formulation of Spin-statistics theorem, and for his contributions to the development of quantum theory, particle physics, and statistical mechanics...
.
There is a version of the Fierz identities for Dirac spinors and there is another version for Weyl spinors. And there are versions for other dimensions besides 3+1 dimensions.
Spinor bilinears can be thought of as elements of a Clifford Algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. Then the Fierz identity is the concrete realization of the relation to the exterior algebra.
The identities for a generic scalar written as the contraction of two Dirac bilinears of the same type can be written with coefficients according the following table.
| Product | S | V | T | A | P | |
|---|---|---|---|---|---|---|
| S × S = | 1/4 | 1/4 | -1/4 | -1/4 | 1/4 | |
| V × V = | 1 | -1/2 | 0 | -1/2 | -1 | |
| T × T = | -3/2 | 0 | -1/2 | 0 | -3/2 | |
| A × A = | -1 | -1/2 | 0 | -1/2 | 1 | |
| P × P = | 1/4 | -1/4 | -1/4 | 1/4 | 1/4 | |
For example the V × V product can be expanded as,
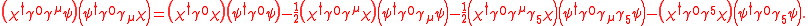
Simplifications arise when the considered spinors are chiral or Majorana spinors as some term in the expansion can be vanishing.

