Fiber diffraction
Encyclopedia
Fiber diffraction is a subarea of scattering
, an area in which molecular structure is determined from scattering data (usually of X-rays, electrons or neutrons). In fiber diffraction the scattering pattern does not change, as the sample is rotated about a unique axis (the fiber axis). Such uniaxial symmetry is frequent with filaments or fibers consisting of biological or man-made macromolecule
s, respectively. In crystallography
fiber symmetry is an aggravation regarding the determination of crystal structure, because reflexions are smeared and may overlap in the fiber diffraction pattern. Materials science
considers fiber symmetry a simplification, because almost the complete obtainable structure information is in a single two-dimensional (2D) diffraction pattern exposed on photographic film or on a 2D detector. 2 instead of 3 co-ordinate directions suffice to describe fiber diffraction.
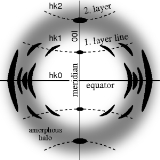
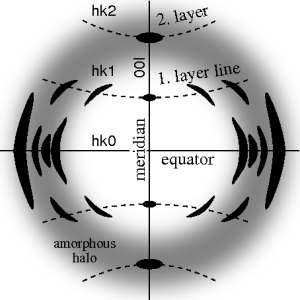The ideal fiber pattern exhibits 4-quadrant symmetry. In the ideal pattern the fiber axis is called the meridian, the perpendicular direction is called equator. In case of fiber symmetry, many more reflexions than in single-crystal diffraction show up in the 2D pattern. In fiber patterns these reflexions clearly appear arranged along lines (layer lines) running almost parallel to the equator. Thus, in fiber diffraction the layer line concept of crystallography
becomes palpable. Bent layer lines indicate that the pattern must be straightened. Reflexions are labelled by the Miller index
hkl, i.e. 3 digits. Reflexions on the i-th layer line share l=i. Reflexions on the meridian are 00l-reflexions. In crystallography
artificial fiber diffraction patterns are generated by rotating a single crystal about an axis (rotating crystal method).
Non-ideal fiber patterns are obtained in experiments. They only show mirror symmetry about the meridian. The reason is that the fiber axis and the incident beam (X-rays, electrons, neutrons) cannot be perfectly oriented perpendicular to each other. The corresponding geometric distortion has been extensively studied by Michael Polanyi
introducing the concept of Polanyi's sphere (German: "Lagenkugel") intersecting Ewald's sphere
. Later Rosalind Franklin
and Raymond Gosling
have carried out their own geometrical reasoning and presented an approximative equation for the fiber tilt angle β. Analysis starts by mapping the distorted 2D pattern on the representative plane of the fiber. This is the plane that contains the cylinder axis in reciprocal space. In crystallography
first an approximation of the mapping into reciprocal space is computed that is refined iteratively. The digital method frequently called Fraser correction starts from the Franklin approximation for the tilt angle β. It eliminates fiber tilt, unwarps the detector image, and corrects the scattering intensity. The correct equation for the determination of β has been presented by Norbert Stribeck.
All science techniques and achievements must be open to scrutiny, assessment and criticism. In the case of fiber diffraction from biological macromolecules, it is evident that the large number of atoms in a molecule far exceeds the number of diffraction "spots" needed to place such atoms in the structure, especially at low resolution. Therefore progress with the structures of such molecules is only possible when the data from x-ray scattering is informed by independent knowledge of the structure which has been gleaned from the use of other techniques and the knowledge derived from them.
This is a main difficulty with x-ray scattering from fibers because the "final" structure of the macromolecule, which includes data derived from the use of other techniques, immediately means that the output from these crystallographers is no longer solely crystallographic but is informed by the modelling ingenuity and any other knowledge held by researchers. Crystallographers should take care to remind their audience of the limitations of the results which can be expected from crystallographic researches.
In the case of DNA fibers, whose structures have been extensively researched using x-ray diffraction, there are numerous other problems to which attention should be drawn. For example, how do we know when the best fiber structure has been deduced ? In the literature there are several groups of crystallographers who disagree with each other about the assessment of the quality of the structures deduced by diffraction from fibers, for example, Bunn, Donohue et al. and Hamilton (see below for detailed references).
Then there is the problem that later researches, generally with a higher resolution than earlier work, nevertheless give rise to structures which are interpreted in terms of the earliest structures, themselves based upon poor, or very poor, resolution allowing the identification of very few "spots".
Further, there is a predeliction for structures deduced by computation of x-ray diffraction data to revert to the starting model, so that new structures are not deduced even when the x-ray data would support them. This phenomenon has been much discussed by, for example, Arnott and Campbell Smith.
X-ray data tends to be interpreted against the chosen starting model. For example, in the famous x-ray diffraction diagram of B-DNA reported by Franklin & Gosling, and in many other similar diagrams (though not in all), the fourth layer line is often missing. This is normally taken to be a consequence of the starting model, a double helix, and to arise from the relative axial displacement of the so-called "major" and "minor" grooves which allegedly give rise to destructive interference at the fourth layer line. Other possibilities are systematically neglected because "an explanation" is confused here with "the explanation."
Crystallographers sometimes seem, temperamentally, to be committed to numerical solution of structural challenges, and thereby to give lesser weight to the results derived from other techniques. By measuring the water content of fibers, for example, it should be possible to compare experimental fiber densities with theoretical values. This is rarely done. A study of "double orientation" in fibers of A-DNA offers fresh insights into the differences between the A form and the B form in which double orientation has never been reported.
Other results are frequently at variance with traditional fiber computational results, for example, those of Langridge and Maurice Wilkins et al. using squared Fourier diagrams, or those of James & Mazia using monomolecular DNA films, to neither of which is reference ever made.
It is evident why crystallographers tend to represent their results as lying beyond challenge, but such a posture does a dis-service to science and to aspiring scientists.
, e.g., the original models of the α-helix
and the Watson-Crick model of double-stranded DNA
.
The animation shows the geometry of fiber diffraction. It is based on the notions proposed by Polanyi. Reference direction is the primary beam (label: X-ray). If the fiber is tilted away from the perpendicular direction by an angle β, as well the information about its molecular structure in reciprocal space (trihedron labelled s-space) is tilted. In reciprocal space the so-called Ewald sphere has its center in the sample. Its radius is 1/λ, with λ the wavelength of the incident radiation. On the surface of the Ewald sphere all the points of reciprocal space are found that are seen by the detector. These points are mapped on the pixels of the detector by central projection.
In s-space each reflexion is found on its Polanyi-sphere. Intrinsically the ideal reflexion is a point in s-space, but fiber symmetry turns it into a ring smeared out by rotation about the fiber direction. Two rings represent each reflexion on the Polanyi sphere, because scattering is point symmetric with respect to the origin of s-space. Mapped onto the detector are only those points of the reflexion in s-space that are both on the Ewald sphere and on the Polanyi sphere. These points form the reflexion circle (blue ring). It does not change as the fiber is tilted. As with a slide projector the reflexion circle is projected (red moving rays) on the detector (detector circle, blue ring). There up to 4 images (red spots) of the monitored reflexion can show up. The position of the reflexion images is a function of the orientation of the fiber in the primary beam (Polanyi equation). Inverted, from the positions of the reflexion images the orientation of the fiber can be determined, if for the Miller index
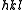both 
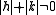and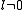 
is valid. From the Polanyi representation of fiber diffraction geometry the relations of the fiber mapping are established by elementary
and spherical geometry.
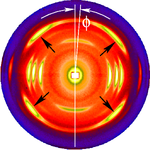
The figure on the left shows a typical fiber pattern of polypropylene
before mapping it into reciprocal space. The mirror axis in the pattern is rotated by the angle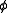
with respect to the vertical direction. This shortcoming is compensated by simple rotation of the picture. 4 straight arrows point at 4 reflexion images of a chosen reference reflexion. Their positions are used to determine the fiber tilt angle 
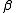. The image has been recorded on a CCD detector. It shows the logarithmic intensitity in pseudo-color representation. Here bright colors represent high intensity.
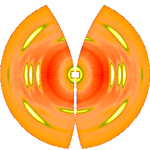
After determination of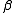
the distance between sample and detector is computed using known crystallographic data of the reference reflexion, a uniformly gridded map for the representative fiber plane in reciprocal space is constructed and the diffraction data are fed into this map. The figure on the right shows the result. Change of scattering intensity has been considered in the unwarping process. Because of the curvature of the surface of the Ewald sphere there remain white spots at the meridian, in which structure information is missing. Only in the center of the image and at a s-value related to the scattering angle 
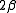there is structure information on the meridian. Of course, there is now 4-quadrant symmetry. This means that in the example pattern part of the missing information may be copied "from the lower half to the upper half" into the white areas. Thus, it frequently makes sense to tilt the fiber intentionally.
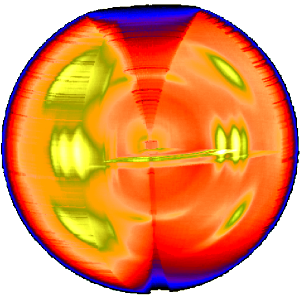The three-dimensional sketch demonstrates that in the example experiment the collected information on the molecular structure of the polypropylene fiber is almost complete. By rotation of the plane pattern about the meridian the scattering data collected in 4 s fill an almost spherical volume of s-space. In the example the 4-quadrant symmetry has not yet been considered to fill part of the white spots. For clarity a quarter of the sphere has been cut out, but keeping the equatorial plane itself.
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
, an area in which molecular structure is determined from scattering data (usually of X-rays, electrons or neutrons). In fiber diffraction the scattering pattern does not change, as the sample is rotated about a unique axis (the fiber axis). Such uniaxial symmetry is frequent with filaments or fibers consisting of biological or man-made macromolecule
Macromolecule
A macromolecule is a very large molecule commonly created by some form of polymerization. In biochemistry, the term is applied to the four conventional biopolymers , as well as non-polymeric molecules with large molecular mass such as macrocycles...
s, respectively. In crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
fiber symmetry is an aggravation regarding the determination of crystal structure, because reflexions are smeared and may overlap in the fiber diffraction pattern. Materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
considers fiber symmetry a simplification, because almost the complete obtainable structure information is in a single two-dimensional (2D) diffraction pattern exposed on photographic film or on a 2D detector. 2 instead of 3 co-ordinate directions suffice to describe fiber diffraction.
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
becomes palpable. Bent layer lines indicate that the pattern must be straightened. Reflexions are labelled by the Miller index
Miller index
Miller indices form a notation system in crystallography for planes and directions in crystal lattices.In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written , and each index denotes a plane orthogonal to a direction in the...
hkl, i.e. 3 digits. Reflexions on the i-th layer line share l=i. Reflexions on the meridian are 00l-reflexions. In crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
artificial fiber diffraction patterns are generated by rotating a single crystal about an axis (rotating crystal method).
Non-ideal fiber patterns are obtained in experiments. They only show mirror symmetry about the meridian. The reason is that the fiber axis and the incident beam (X-rays, electrons, neutrons) cannot be perfectly oriented perpendicular to each other. The corresponding geometric distortion has been extensively studied by Michael Polanyi
Michael Polanyi
Michael Polanyi, FRS was a Hungarian–British polymath, who made important theoretical contributions to physical chemistry, economics, and the theory of knowledge...
introducing the concept of Polanyi's sphere (German: "Lagenkugel") intersecting Ewald's sphere
Ewald's sphere
The Ewald sphere is a geometric construct used in electron, neutron, and X-ray crystallography which demonstrates the relationship between:* the wavevector of the incident and diffracted x-ray beams,* the diffraction angle for a given reflection,...
. Later Rosalind Franklin
Rosalind Franklin
Rosalind Elsie Franklin was a British biophysicist and X-ray crystallographer who made critical contributions to the understanding of the fine molecular structures of DNA, RNA, viruses, coal and graphite...
and Raymond Gosling
Raymond Gosling
Raymond Gosling is a distinguished scientist who worked with both Maurice Wilkins and Rosalind Franklin at King's College London in deducing the structure of DNA, under the direction of Sir John Randall. His other KCL colleagues included Alex Stokes and Herbert Wilson.-Early years:He was born in...
have carried out their own geometrical reasoning and presented an approximative equation for the fiber tilt angle β. Analysis starts by mapping the distorted 2D pattern on the representative plane of the fiber. This is the plane that contains the cylinder axis in reciprocal space. In crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
first an approximation of the mapping into reciprocal space is computed that is refined iteratively. The digital method frequently called Fraser correction starts from the Franklin approximation for the tilt angle β. It eliminates fiber tilt, unwarps the detector image, and corrects the scattering intensity. The correct equation for the determination of β has been presented by Norbert Stribeck.
All science techniques and achievements must be open to scrutiny, assessment and criticism. In the case of fiber diffraction from biological macromolecules, it is evident that the large number of atoms in a molecule far exceeds the number of diffraction "spots" needed to place such atoms in the structure, especially at low resolution. Therefore progress with the structures of such molecules is only possible when the data from x-ray scattering is informed by independent knowledge of the structure which has been gleaned from the use of other techniques and the knowledge derived from them.
This is a main difficulty with x-ray scattering from fibers because the "final" structure of the macromolecule, which includes data derived from the use of other techniques, immediately means that the output from these crystallographers is no longer solely crystallographic but is informed by the modelling ingenuity and any other knowledge held by researchers. Crystallographers should take care to remind their audience of the limitations of the results which can be expected from crystallographic researches.
In the case of DNA fibers, whose structures have been extensively researched using x-ray diffraction, there are numerous other problems to which attention should be drawn. For example, how do we know when the best fiber structure has been deduced ? In the literature there are several groups of crystallographers who disagree with each other about the assessment of the quality of the structures deduced by diffraction from fibers, for example, Bunn, Donohue et al. and Hamilton (see below for detailed references).
Then there is the problem that later researches, generally with a higher resolution than earlier work, nevertheless give rise to structures which are interpreted in terms of the earliest structures, themselves based upon poor, or very poor, resolution allowing the identification of very few "spots".
Further, there is a predeliction for structures deduced by computation of x-ray diffraction data to revert to the starting model, so that new structures are not deduced even when the x-ray data would support them. This phenomenon has been much discussed by, for example, Arnott and Campbell Smith.
X-ray data tends to be interpreted against the chosen starting model. For example, in the famous x-ray diffraction diagram of B-DNA reported by Franklin & Gosling, and in many other similar diagrams (though not in all), the fourth layer line is often missing. This is normally taken to be a consequence of the starting model, a double helix, and to arise from the relative axial displacement of the so-called "major" and "minor" grooves which allegedly give rise to destructive interference at the fourth layer line. Other possibilities are systematically neglected because "an explanation" is confused here with "the explanation."
Crystallographers sometimes seem, temperamentally, to be committed to numerical solution of structural challenges, and thereby to give lesser weight to the results derived from other techniques. By measuring the water content of fibers, for example, it should be possible to compare experimental fiber densities with theoretical values. This is rarely done. A study of "double orientation" in fibers of A-DNA offers fresh insights into the differences between the A form and the B form in which double orientation has never been reported.
Other results are frequently at variance with traditional fiber computational results, for example, those of Langridge and Maurice Wilkins et al. using squared Fourier diagrams, or those of James & Mazia using monomolecular DNA films, to neither of which is reference ever made.
It is evident why crystallographers tend to represent their results as lying beyond challenge, but such a posture does a dis-service to science and to aspiring scientists.
Historical role
Fiber diffraction data led to several important advances in the development of structural biologyStructural biology
Structural biology is a branch of molecular biology, biochemistry, and biophysics concerned with the molecular structure of biological macromolecules, especially proteins and nucleic acids, how they acquire the structures they have, and how alterations in their structures affect their function...
, e.g., the original models of the α-helix
Alpha helix
A common motif in the secondary structure of proteins, the alpha helix is a right-handed coiled or spiral conformation, in which every backbone N-H group donates a hydrogen bond to the backbone C=O group of the amino acid four residues earlier...
and the Watson-Crick model of double-stranded DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
.
Fiber diffraction geometry
In s-space each reflexion is found on its Polanyi-sphere. Intrinsically the ideal reflexion is a point in s-space, but fiber symmetry turns it into a ring smeared out by rotation about the fiber direction. Two rings represent each reflexion on the Polanyi sphere, because scattering is point symmetric with respect to the origin of s-space. Mapped onto the detector are only those points of the reflexion in s-space that are both on the Ewald sphere and on the Polanyi sphere. These points form the reflexion circle (blue ring). It does not change as the fiber is tilted. As with a slide projector the reflexion circle is projected (red moving rays) on the detector (detector circle, blue ring). There up to 4 images (red spots) of the monitored reflexion can show up. The position of the reflexion images is a function of the orientation of the fiber in the primary beam (Polanyi equation). Inverted, from the positions of the reflexion images the orientation of the fiber can be determined, if for the Miller index
Miller index
Miller indices form a notation system in crystallography for planes and directions in crystal lattices.In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written , and each index denotes a plane orthogonal to a direction in the...
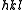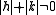both and 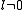is valid. From the Polanyi representation of fiber diffraction geometry the relations of the fiber mapping are established by elementaryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and spherical geometry.
Pattern correction
Polypropylene
Polypropylene , also known as polypropene, is a thermoplastic polymer used in a wide variety of applications including packaging, textiles , stationery, plastic parts and reusable containers of various types, laboratory equipment, loudspeakers, automotive components, and polymer banknotes...
before mapping it into reciprocal space. The mirror axis in the pattern is rotated by the angle
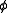with respect to the vertical direction. This shortcoming is compensated by simple rotation of the picture. 4 straight arrows point at 4 reflexion images of a chosen reference reflexion. Their positions are used to determine the fiber tilt angle 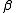. The image has been recorded on a CCD detector. It shows the logarithmic intensitity in pseudo-color representation. Here bright colors represent high intensity.After determination of
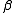the distance between sample and detector is computed using known crystallographic data of the reference reflexion, a uniformly gridded map for the representative fiber plane in reciprocal space is constructed and the diffraction data are fed into this map. The figure on the right shows the result. Change of scattering intensity has been considered in the unwarping process. Because of the curvature of the surface of the Ewald sphere there remain white spots at the meridian, in which structure information is missing. Only in the center of the image and at a s-value related to the scattering angle 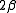there is structure information on the meridian. Of course, there is now 4-quadrant symmetry. This means that in the example pattern part of the missing information may be copied "from the lower half to the upper half" into the white areas. Thus, it frequently makes sense to tilt the fiber intentionally.Text books
- Alexander LE (1979) "X-Ray Diffraction Methods in Polymer Science", Wiley, New York
- Klug HP, Alexander LE (1974) "X-Ray Diffraction Procedures For Polycrystalline and Amorphous Materials", 2nd ed, Wiley, New York
- Warren BE (1990) "X-Ray Diffraction". Dover, New York
External links
- Fibre Diffraction Review — Publications of the CCP13 Fibre Diffraction Software Project
- FibreFix — Windows software for the analysis of fiber patterns
- WCEN — Software (Linux, Mac, Windows) for the analysis of fiber patterns
- Fiber Diffraction — an introduction provided by Prof. K.C. Holmes, Max Planck Institute for Medical Research, Heidelberg.