Fermat's little theorem
Encyclopedia
Fermat's little theorem (so named to distinguish it from Fermat's last theorem
) states that if p is a prime number
, then for any integer
a, a p − a will be evenly divisible by p. This can be expressed in the notation of modular arithmetic
as follows:
A variant of this theorem is stated in the following form: if p is a prime and a is an integer coprime
to p, then a p−1 − 1 will be evenly divisible by p. In the notation of modular arithmetic:
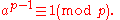
Fermat's little theorem is the basis for the Fermat primality test
. The theorem is named after Pierre de Fermat
.
Pierre de Fermat
first stated the theorem in a letter dated October 18, 1640, to his friend and confidant Frénicle de Bessy as the following: p divides a p−1 − 1 whenever p is prime and a is coprime
to p.
As usual, Fermat did not prove his assertion, only stating:
Euler first published a proof in 1736 in a paper entitled "Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio", but Leibniz
left virtually the same proof in an unpublished manuscript from sometime before 1683.
The term "Fermat's Little Theorem" was first used in 1913 in Zahlentheorie by Kurt Hensel
:
It was first used in English in an article by Irving Kaplansky
, "Lucas
's Tests for Mersenne Numbers," American Mathematical Monthly
, 52 (Apr., 1945).
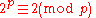. This is a special case of Fermat's little theorem. However, the "if" part of this hypothesis is false: for example, 
, but 341 = 11 × 31 is a pseudoprime
. See below.
in a manuscript without a date, where he wrote also that he knew a proof before 1683.
then 
.
This follows as m is of the form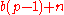
, so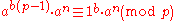 
.
In this form, the theorem is used to justify the RSA public key encryption method.
Fermat's little theorem is generalized by Euler's theorem: for any modulus
n and any integer a coprime
to n, we have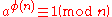
where φ(n) denotes Euler's totient function
counting the integers between 1 and n that are coprime to n. This is indeed a generalization, because if n = p is a prime number, then φ(p) = p − 1.
This can be further generalized to Carmichael's theorem.
The theorem also has a nice generalization in finite field
s.
to base a. F. Sarrus in 1820 found 341 = 11 × 31 as one of the first pseudoprimes, to base 2.
A number p that is a pseudoprime to base a for every number a coprime to p is called a Carmichael number (e.g. 561). Alternately, any number satisfying the equality
is either a prime or Carmichael number.
If there exists an a such that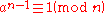
and for all prime q dividing n-1
then n is prime.
This theorem forms the basis for the Lucas-Lehmer test, an important primality test
.
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
) states that if p is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, then for any integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
a, a p − a will be evenly divisible by p. This can be expressed in the notation of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
as follows:
A variant of this theorem is stated in the following form: if p is a prime and a is an integer coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to p, then a p−1 − 1 will be evenly divisible by p. In the notation of modular arithmetic:
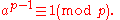
Fermat's little theorem is the basis for the Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
. The theorem is named after Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
.
History
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
first stated the theorem in a letter dated October 18, 1640, to his friend and confidant Frénicle de Bessy as the following: p divides a p−1 − 1 whenever p is prime and a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to p.
As usual, Fermat did not prove his assertion, only stating:
Et cette proposition est généralement vraie en toutes progressions et en tous nombres premiers; de quoi je vous envoierois la démonstration, si je n'appréhendois d'être trop long.
(And this proposition is generally true for all progressions and for all prime numbers; the proof of which I would send to you, if I were not afraid to be too long.)
Euler first published a proof in 1736 in a paper entitled "Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio", but Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
left virtually the same proof in an unpublished manuscript from sometime before 1683.
The term "Fermat's Little Theorem" was first used in 1913 in Zahlentheorie by Kurt Hensel
Kurt Hensel
Kurt Wilhelm Sebastian Hensel was a German mathematician born in Königsberg, Prussia.He was the son of the landowner and entrepreneur Sebastian Hensel, brother of the philosopher Paul Hensel, grandson of the composer Fanny Mendelssohn and the painter Wilhelm Hensel, and a descendant of the...
:
Für jede endliche Gruppe besteht nun ein Fundamentalsatz, welcher der kleine Fermatsche Satz genannt zu werden pflegt, weil ein ganz spezieller Teil desselben zuerst von Fermat bewiesen worden ist."
(There is a fundamental theorem holding in every finite group, usually called Fermat's little Theorem because Fermat was the first to have proved a very special part of it.)
It was first used in English in an article by Irving Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
, "Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
's Tests for Mersenne Numbers," American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
, 52 (Apr., 1945).
Further history
Some mathematicians independently made the related hypothesis (sometimes incorrectly called the Chinese Hypothesis) that p is a prime if and only if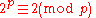. This is a special case of Fermat's little theorem. However, the "if" part of this hypothesis is false: for example, , but 341 = 11 × 31 is a pseudoprimePseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
. See below.
Proofs
Fermat gave his theorem without a proof. The first one who gave a proof was Gottfried LeibnizGottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
in a manuscript without a date, where he wrote also that he knew a proof before 1683.
Generalizations
A slight generalization of the theorem, which immediately follows from it, is: if p is prime and m and n are positive integers such that then .This follows as m is of the form
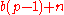, so 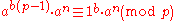.In this form, the theorem is used to justify the RSA public key encryption method.
Fermat's little theorem is generalized by Euler's theorem: for any modulus
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n and any integer a coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n, we have
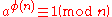
where φ(n) denotes Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
counting the integers between 1 and n that are coprime to n. This is indeed a generalization, because if n = p is a prime number, then φ(p) = p − 1.
This can be further generalized to Carmichael's theorem.
The theorem also has a nice generalization in finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Pseudoprimes
If a and p are coprime numbers such that a p−1 − 1 is divisible by p, then p need not be prime. If it is not, then p is called a pseudoprimePseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
to base a. F. Sarrus in 1820 found 341 = 11 × 31 as one of the first pseudoprimes, to base 2.
A number p that is a pseudoprime to base a for every number a coprime to p is called a Carmichael number (e.g. 561). Alternately, any number satisfying the equality
is either a prime or Carmichael number.
Converse
The converse of Fermat's little theorem is not generally true, as it fails for Carmichael numbers. However, a slightly stronger form of the theorem is true, and is known as Lehmer's theorem. The theorem is as follows:If there exists an a such that
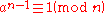
and for all prime q dividing n-1
then n is prime.
This theorem forms the basis for the Lucas-Lehmer test, an important primality test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
.
See also
- Fractions with prime denominators–numbers with behavior relating to Fermat's little theorem
- RSA
- p-derivationP-derivationIn mathematics, more specifically differential algebra, a p-derivation on a ring R, is a mapping from R to R that satisfies certain conditions outlined directly below. The notion of a p-derivation is related to that of a derivation in differential algebra.-Definition:Let p be a prime number...
- Frobenius endomorphismFrobenius endomorphismIn commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
External links
- Fermat's Little Theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Euler Function and Theorem at cut-the-knot
- Fermat's Little Theorem and Sophie's Proof
- Text and translation of Fermat's letter to Frenicle