Fast Kalman filter
Encyclopedia
The fast Kalman filter, devised by Antti Lange
(1941- ), is an extension of the Helmert-Wolf blocking
(HWB) method from geodesy
to real-time applications of Kalman filter
ing (KF) such as satellite imaging of the Earth. Kalman filters are an important software technique for building fault-tolerance into a wide range of systems, including real-time imaging.
The ordinary Kalman filter is optimal for general systems. However, an optimal Kalman filter is probably stable only if Kalman's observability and controllability conditions are also satisfied (Kalman, 1960). These conditions are challenging to continuously maintain for a large system which means that even an optimal Kalman filter may diverge towards false solutions. Fortunately, the stability of an optimal Kalman filter can be controlled by monitoring its error variances if these can be reliably estimated. Their precise computation is, however, much more demanding than the optimal filtering itself but the FKF method may provide the required speed-up also in this respect.
of an ordinary Kalman recursion is roughly proportional to the cube of the number of the measurements processed simultaneously, which can always be set to 1 by processing each scalar measurement independently and (if necessary) performing a simple pre-filtering algorithm to de-correlate these measurements.
Even when many measurements are processed simultaneously, it is not unusual that the linear equation system is sparse, because some measurements turn out to be independent of some state or calibration parameters.
In Satellite Geodesy problems (Brockmann, 1997), the computing load of the HWB
(and FKF) method is only roughly proportional to the square of the number of the state parameters (and not of the measurements whose number may be billions).
is obtained by matrix inversion from the respective system of Normal Equations. Its coefficient matrix is usually sparse and the exact solution of all estimated parameters can be computed by using the HWB method. The optimal solution may also be obtained by Gauss elimination using other sparse-matrix techniques or iterative methods based e.g. on Variational Calculus
.
However, these latter methods can solve the large matrix of all error variances and covariances only approximately and it would thus be impossible to do the data fusion in a strictly optimal fashion. Consequently, the filter's stability may become uncertain even if the observability and controllability conditions were satisfied.
The sparse coefficient matrix to be inverted may often have either a bordered block- or band-diagonal (BBD) structure. If it is band-diagonal it can be transformed into a block-diagonal form e.g. by means of a generalised Canonical Correlation Analysis (gCCA)
. The large matrix can thus be most effectively inverted in a blockwise manner by using the following
analytic inversion formula: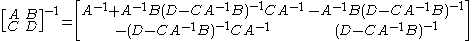
of Frobenius
where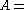
a large block- or band-diagonal (BD) matrix to be easily inverted, and,
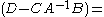a much smaller matrix called the Schur
complement of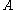
.
This is the FKF method that may make it computationally possible to estimate a much larger number of state and calibration parameters than an ordinary Kalman recursion can do. Their operational accuracies may also be reliably estimated from the theory of Minimum-Norm Quadratic Unbiased Estimation (MINQUE
) of C. R. Rao
(1920- ) and used for controlling the stability of optimal Kalman filtering.
(RTK) surveying, mobile positioning and ultra-reliable navigation (Lange, 2003). First important applications will be real-time optimum calibration of global observing systems in Meteorology, Geophysics, Astronomy etc.
For example, a Numerical Weather Prediction
(NWP) system can now forecast observations with confidence intervals and their operational quality control can thus be improved. A sudden increase of uncertainty in predicting observations would indicate that important observations were missing (observability problem) or an unpredictable change of weather is taking place (controllability problem). Remote sensing and imaging from satellites may partly be based on forecast information. Controlling stability of such feedback between the forecast and satellite data calls for the theory of optimal Kalman filtering. No suboptimal solution would do a proper job as public safety is usually at stake.
The computational advantage of FKF is marginal for applications using only small amounts of data in real-time data. Therefore improved built-in calibration and data communication infrastructures need to be developed first and introduced to public use before personal gadgets and machine-to-machine (M2M) devices can make the best out of FKF.
Antti Lange
Antti Lange is a Finnish mathematician andstatistician of the Finnish Meteorological Institute. Previous employers included ECMWF, WMO, Helsinki University and the University of Jyväskylä.-External links:*...
(1941- ), is an extension of the Helmert-Wolf blocking
Helmert-Wolf blocking
The Helmert–Wolf blocking is a least squares solution for a sparse system of linear equations. Friedrich Robert Helmert reported on the use of such systems for geodesy in his book "Die mathematischen und physikalischen Theorieen der höheren Geodäsie, 1. Teil" published in Leipzig, 1880...
(HWB) method from geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
to real-time applications of Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
ing (KF) such as satellite imaging of the Earth. Kalman filters are an important software technique for building fault-tolerance into a wide range of systems, including real-time imaging.
Description
The Fast Kalman filter applies only to systems with sparse matrices (Lange, 2001), since HWB is an inversion method to solve sparse linear equations (Wolf, 1978).The ordinary Kalman filter is optimal for general systems. However, an optimal Kalman filter is probably stable only if Kalman's observability and controllability conditions are also satisfied (Kalman, 1960). These conditions are challenging to continuously maintain for a large system which means that even an optimal Kalman filter may diverge towards false solutions. Fortunately, the stability of an optimal Kalman filter can be controlled by monitoring its error variances if these can be reliably estimated. Their precise computation is, however, much more demanding than the optimal filtering itself but the FKF method may provide the required speed-up also in this respect.
Optimum calibration
Calibration parameters are a typical example of those state parameters that may create serious observability problems if a narrow window of data (i.e. too few measurements) is continuously used by a Kalman filter (Lange, 1999). Observing instruments onboard orbiting satellites gives an example of optimal Kalman filtering where their calibration is done indirectly on ground (Olsson el al, 2001). There may also exist other state parameters that are hardly or not at all observable (estimable) if too small samples of data are processed (analysed) at a time by any sort of a Kalman filter.Inverse problem
The computing load of the inverse problemInverse problem
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
of an ordinary Kalman recursion is roughly proportional to the cube of the number of the measurements processed simultaneously, which can always be set to 1 by processing each scalar measurement independently and (if necessary) performing a simple pre-filtering algorithm to de-correlate these measurements.
Even when many measurements are processed simultaneously, it is not unusual that the linear equation system is sparse, because some measurements turn out to be independent of some state or calibration parameters.
In Satellite Geodesy problems (Brockmann, 1997), the computing load of the HWB
(and FKF) method is only roughly proportional to the square of the number of the state parameters (and not of the measurements whose number may be billions).
Reliable solution
Reliable operational Kalman filtering requires continuous fusion of data in real-time. Its optimality depends essentially on use of the error variances and covariances between all measurements and the estimated state and calibration parameters. This large error covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
is obtained by matrix inversion from the respective system of Normal Equations. Its coefficient matrix is usually sparse and the exact solution of all estimated parameters can be computed by using the HWB method. The optimal solution may also be obtained by Gauss elimination using other sparse-matrix techniques or iterative methods based e.g. on Variational Calculus
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
.
However, these latter methods can solve the large matrix of all error variances and covariances only approximately and it would thus be impossible to do the data fusion in a strictly optimal fashion. Consequently, the filter's stability may become uncertain even if the observability and controllability conditions were satisfied.
The sparse coefficient matrix to be inverted may often have either a bordered block- or band-diagonal (BBD) structure. If it is band-diagonal it can be transformed into a block-diagonal form e.g. by means of a generalised Canonical Correlation Analysis (gCCA)
Generalized canonical correlation
In statistics, the generalized canonical correlation analysis , is a way of making sense of cross-correlation matrices between the sets of random variables when there are more than two sets. While a conventional CCA generalizes Principal component analysis to two sets of random variables, a gCCA ...
. The large matrix can thus be most effectively inverted in a blockwise manner by using the following
analytic inversion formula:
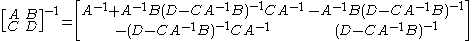
of Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
where
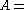a large block- or band-diagonal (BD) matrix to be easily inverted, and, 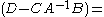a much smaller matrix called the SchurIssai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
complement of
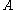.This is the FKF method that may make it computationally possible to estimate a much larger number of state and calibration parameters than an ordinary Kalman recursion can do. Their operational accuracies may also be reliably estimated from the theory of Minimum-Norm Quadratic Unbiased Estimation (MINQUE
Minque
In statistics, the theory of minimum norm quadratic unbiased estimation was developed by C.R. Rao. Its application was originally to the estimation of variance components in random effects models.The theory involves three stages:...
) of C. R. Rao
C. R. Rao
Calyampudi Radhakrishna Rao FRS known as C R Rao is an Indian statistician. He is currently professor emeritus at Penn State University and Research Professor at the University at Buffalo. Rao has been honored by numerous colloquia, honorary degrees, and festschrifts and was awarded the US...
(1920- ) and used for controlling the stability of optimal Kalman filtering.
Applications
The FKF method extends the very high accuracies of Satellite Geodesy to Virtual Reference Station (VRS) Real Time KinematicReal Time Kinematic
Real Time Kinematic satellite navigation is a technique used in land survey and in hydrographic survey based on the use of carrier phase measurements of the GPS, GLONASS and/or Galileo signals where a single reference station provides the real-time corrections, providing up to centimetre-level...
(RTK) surveying, mobile positioning and ultra-reliable navigation (Lange, 2003). First important applications will be real-time optimum calibration of global observing systems in Meteorology, Geophysics, Astronomy etc.
For example, a Numerical Weather Prediction
Numerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
(NWP) system can now forecast observations with confidence intervals and their operational quality control can thus be improved. A sudden increase of uncertainty in predicting observations would indicate that important observations were missing (observability problem) or an unpredictable change of weather is taking place (controllability problem). Remote sensing and imaging from satellites may partly be based on forecast information. Controlling stability of such feedback between the forecast and satellite data calls for the theory of optimal Kalman filtering. No suboptimal solution would do a proper job as public safety is usually at stake.
The computational advantage of FKF is marginal for applications using only small amounts of data in real-time data. Therefore improved built-in calibration and data communication infrastructures need to be developed first and introduced to public use before personal gadgets and machine-to-machine (M2M) devices can make the best out of FKF.
External links
- BBD - software
- FKF - formulas
- HWB - formulas
- The error covariance matrix of FKF - formulas
- There are other Fast Kalman Algorithms designed for special signal processing purposes, see e.g. Stabilizing the Fast Kalman Algorithms on IEEE Xplore
- Kalman filter recipes for real-time image processing