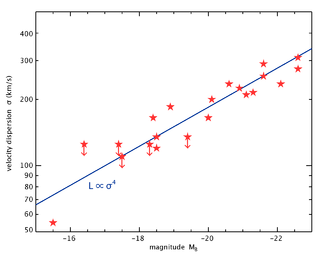
Faber-Jackson relation
Encyclopedia
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
power-law relation between the luminosity
Luminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
and the central stellarStar
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
velocity dispersion
Velocity dispersion
In astronomy, the velocity dispersion σ, is the range of velocities about the mean velocity for a group of objects, such as a cluster of stars about a galaxy...
of elliptical galaxiesElliptical galaxy
An elliptical galaxy is a galaxy having an approximately ellipsoidal shape and a smooth, nearly featureless brightness profile. They range in shape from nearly spherical to highly flat and in size from hundreds of millions to over one trillion stars...
, first noted by the astronomers Sandra M. Faber
Sandra M. Faber
Sandra Moore Faber is a University Professor of Astronomy and Astrophysics at the University of California, Santa Cruz, and works at the Lick Observatory.In 1966, she obtained a B.A., with high honors, in physics from Swarthmore College....
and Robert Earl Jackson
Robert Jackson (scientist)
Robert Earl Jackson is a scientist, who, with Sandra M. Faber, in 1976 discovered the Faber-Jackson relation between the luminosity of an elliptical galaxy and the velocity dispersion in its center....
in 1976. The original relation can be expressed mathematically as:
where the index
is observed to be approximately equal to 4, but depends on the range of galaxy luminosities that is fitted. The Faber–Jackson relation is now understood as a projection of the fundamental planeFundamental plane (elliptical galaxies)
The fundamental plane is a relationship between the effective radius, average surface brightness and central velocity dispersion of normal elliptical galaxies. Any one of the three parameters may be estimated from the other two, as together they describe a plane that falls within their more...
of elliptical galaxies. One of its main uses is as a tool for determining distances to external galaxies.
Theory
The gravitational potentialGravitational binding energy
The gravitational binding energy of an object consisting of loose material, held together by gravity alone, is the amount of energy required to pull all of the material apart, to infinity...
of a mass distribution of radius
and mass 
is given by the expression:
Where α is a constant depending e.g. on the density profile of the system. For a constant density, α =
The kinetic energy is (recall
is the 1 dimensional velocity dispersion. Therefore 3
2 = V2):
From the Virial Theorem (
) it follows
.If we assume that the mass to light ratio,
, is constant, e.g. 
we can use this and the above expression to obtain a relation between 
and 
:
.Let us introduce the surface brightness,
and assume this is a constant to get
.Using this and combining it with the relation between
and 
, this results in
and by rewriting the above expression, we finally obtain the relation between luminosity and velocity dispersion:
,that is
.When account is taken of the fact that massive galaxies originate from homologous merging, and the fainter ones from dissipation, the assumption of constant surface brightness can no longer be supported. Empirically, surface brightness exhibits a peak at about
. The revised relation then becomes
for the less massive galaxies, and
for the more massive ones. With these revised formulae, the fundamental plane splits into two planes inclined by about 11 degrees to each other.
Even first-ranked cluster galaxies do not have constant surface brightness. A claim supporting constant surface brightness was presented by astronomer Allan R. Sandage in 1972 based on three logical arguments and his own empirical data. In 1975, Donald Gudehus showed that each of the logical arguments was incorrect and that first-ranked cluster galaxies exhibited a standard deviation of about half a magnitude.
Estimating distances to galaxies
Like the Tully-Fisher relation, the Faber–Jackson relation provides a means of estimating the distance to a galaxy, which is otherwise hard to obtain, by relating it to more easily observable properties of the galaxy. In the case of elliptical galaxies, if one can measure the central stellar velocity dispersion, which can be done relatively easily by using spectroscopySpectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
to measure the Doppler shift of light emitted by the stars, then one can obtain an estimate of the true luminosity of the galaxy via the Faber–Jackson relation. This can be compared to the apparent magnitude
Apparent magnitude
The apparent magnitude of a celestial body is a measure of its brightness as seen by an observer on Earth, adjusted to the value it would have in the absence of the atmosphere...
of the galaxy, which provides an estimate of the distance modulus
Distance modulus
-Definition:The distance modulus \mu=m-M is the difference between the apparent magnitude m and the absolute magnitude M of an astronomical object...
and, hence, the distance to the galaxy.
By combining a galaxy's central velocity dispersion with measurements of its central surface brightness and radius parameter, it is possible to improve the estimate of the galaxy's distance even more. This standard yardstick, or "reduced galaxian radius-parameter",
, devised by Gudehus in 1991, can yield distances, free of systematic bias, accurate to about 31%.See also
- Fundamental plane (elliptical galaxies)Fundamental plane (elliptical galaxies)The fundamental plane is a relationship between the effective radius, average surface brightness and central velocity dispersion of normal elliptical galaxies. Any one of the three parameters may be estimated from the other two, as together they describe a plane that falls within their more...
- Tully–Fisher relation
- M-sigma relationM-sigma relationThe M-sigma relation is an empirical correlation between the stellar velocity dispersion \sigma of a galaxy bulge and the mass M of the supermassive black hole atthe galaxy's center.The relation can be expressed mathematically as...