Ex-tangential quadrilateral
Encyclopedia
In Euclidean geometry
, an ex-tangential quadrilateral is a convex
quadrilateral
where the extensions of all four sides are tangent to a circle
outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the exradius and its center the excenter (E in the figure). The excenter lies at the intersection of the angle bisectors to the exterior angles at the extensions of the sides and the sides extended. The ex-tangential quadrilateral is closely related to the tangential quadrilateral
(where the four sides are tangent to a circle).
are examples of ex-tangential quadrilaterals. Parallelograms (which include squares
, rhombi
, and rectangle
s) can be considered ex-tangential quadrilaterals with infinite
exradius since they satisfy the characterizations in the next section, but the excircle cannot be tangent to both pairs of extensions of opposite sides (since they are parallel). Convex quadrilaterals whose side lengths form an arithmetic progression
are always ex-tangential as they satisfy the characterization below for adjacent side lengths.
or as 
. This was proved by Jacob Steiner in 1846. A way of combining these characterizations is that the absolute value
s of the differences between opposite sides are equal for the two pairs of opposite sides. (These equations are closely related to the Pitot theorem
for tangential quadrilateral
s, where the sums of opposite sides are equal for the two pairs of opposite sides.)
The implication to the right is named after L. M. Urquhart (1902-1966) although it was proved long before by Augustus De Morgan
in 1841. Daniel Pedoe
named it the most elementary theorem in Euclidean geometry
since it only concerns straight lines and distances. That there in fact is an equivalence was proved by Mowaffac Hajja, which makes the equality to the right another necessary and sufficient condition for a quadrilateral to be ex-tangential.
Note that this is the same formula as the one for the area of a tangential quadrilateral
and it is also derived from Bretschneider's formula in the same way.
, its area is given by
which is the same as for a bicentric quadrilateral
.
If x is the distance between the circumcenter and the excenter, then
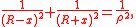
where R and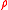
are the circumradius and exradius respectively. This is the same equation as Fuss' theorem for a bicentric quadrilateral. But when solving for x, we must choose the other root of the quadratic equation
for the ex-bicentric quadrilateral compared to the bicentric. Hence, for the ex-bicentric we have
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, an ex-tangential quadrilateral is a convex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
where the extensions of all four sides are tangent to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the exradius and its center the excenter (E in the figure). The excenter lies at the intersection of the angle bisectors to the exterior angles at the extensions of the sides and the sides extended. The ex-tangential quadrilateral is closely related to the tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
(where the four sides are tangent to a circle).
Special cases
KitesKite (geometry)
In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
are examples of ex-tangential quadrilaterals. Parallelograms (which include squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, rhombi
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
, and rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s) can be considered ex-tangential quadrilaterals with infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
exradius since they satisfy the characterizations in the next section, but the excircle cannot be tangent to both pairs of extensions of opposite sides (since they are parallel). Convex quadrilaterals whose side lengths form an arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
are always ex-tangential as they satisfy the characterization below for adjacent side lengths.
Characterizations
A convex quadrilateral with sides a, b, c, d is ex-tangential if and only if the sum of two adjacent sides is equal to the sum of the other two sides. This is possible in two different ways—either as or as . This was proved by Jacob Steiner in 1846. A way of combining these characterizations is that the absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
s of the differences between opposite sides are equal for the two pairs of opposite sides. (These equations are closely related to the Pitot theorem
Pitot theorem
In geometry, the Pitot theorem, named after the French engineer Henri Pitot, states that in a tangential quadrilateral the two sums of lengths of opposite sides are the same. The theorem is a consequence of the fact that two tangent line segments from a point outside the circle to the circle have...
for tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
s, where the sums of opposite sides are equal for the two pairs of opposite sides.)
Urquhart’s Theorem
If opposite sides in a convex quadrilateral ABCD intersect at E and F, thenThe implication to the right is named after L. M. Urquhart (1902-1966) although it was proved long before by Augustus De Morgan
Augustus De Morgan
Augustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....
in 1841. Daniel Pedoe
Daniel Pedoe
Dan Pedoe was an English-born mathematician and geometer with a career spanning more than sixty years. In the course of his life he wrote approximately fifty research and expository papers in geometry. He is also the author of various core books on mathematics and geometry some of which have...
named it the most elementary theorem in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
since it only concerns straight lines and distances. That there in fact is an equivalence was proved by Mowaffac Hajja, which makes the equality to the right another necessary and sufficient condition for a quadrilateral to be ex-tangential.
Area
An ex-tangential quadrilateral ABCD with sides a, b, c, d has the areaNote that this is the same formula as the one for the area of a tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
and it is also derived from Bretschneider's formula in the same way.
Ex-bicentric quadrilateral
If an ex-tangential quadrilateral also has a circumcircle, it is called an ex-bicentric quadrilateral. Then, since it has two opposite supplementary anglesSupplementary angles
Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....
, its area is given by
which is the same as for a bicentric quadrilateral
Bicentric quadrilateral
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...
.
If x is the distance between the circumcenter and the excenter, then
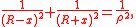
where R and
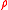are the circumradius and exradius respectively. This is the same equation as Fuss' theorem for a bicentric quadrilateral. But when solving for x, we must choose the other root of the quadratic equationQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
for the ex-bicentric quadrilateral compared to the bicentric. Hence, for the ex-bicentric we have
See also
- Bicentric quadrilateralBicentric quadrilateralIn Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...
- Cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
- KiteKite (geometry)In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
- Orthodiagonal quadrilateralOrthodiagonal quadrilateralIn Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal to each other....
- RhombusRhombusIn Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
- Tangential quadrilateralTangential quadrilateralIn Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
- Complete quadrangle