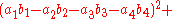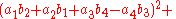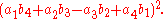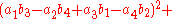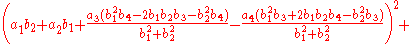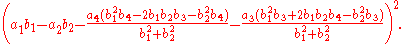Euler's four-square identity
Encyclopedia
In mathematics
, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:
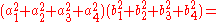
Euler
wrote about this identity in a letter dated May 4, 1748 to Goldbach
(but note that he used a different sign convention from the above). It can be proven with elementary algebra
and holds in every commutative ring
. If the and
and  are real number
are real number
s, a more elegant proof is available: the identity expresses the fact that the absolute value of the product of two quaternion
s is equal to the product of their absolute values, in the same way that the Brahmagupta-Fibonacci two-square identity
does for complex numbers.
The identity was used by Lagrange
to prove his four square theorem
. More specifically, it implies that it is sufficient to prove the theorem for prime numbers, after which the more general theorem follows. The sign convention used above corresponds to the signs obtained by multiplying two quaternions. Other sign conventions can be obtained by changing any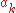 to
to 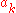 ,
, 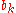 to
to 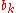 , or by changing the signs inside any of the squared terms on the right hand side.
, or by changing the signs inside any of the squared terms on the right hand side.
However, a different kind of four-square identity can be given as,
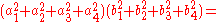
More generally, while Hurwitz's theorem states that an identity of form,
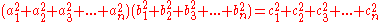
where the are bilinear
are bilinear
functions of the and
and  is possible only for n = {1, 2, 4, 8}, the more general Pfister's theorem allows that if the
is possible only for n = {1, 2, 4, 8}, the more general Pfister's theorem allows that if the  are just rational functions of one set of variables (in this case, the
are just rational functions of one set of variables (in this case, the 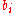 ), hence has a denominator, then it is possible for all
), hence has a denominator, then it is possible for all 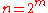 .
.
A,B, and C be the Coefficients of four Binary Quartic Forms,
whose Variables are , and
, and 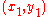
Also let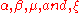 be any quantities desired. Then
be any quantities desired. Then
The derivation of this is done in pure algebra.
The algebra needed to derive this Identity can be found in a PDF file called the
Generalization of Euler's Four Squares (about 60 pages ). It can be found at http://www.samz.us
Notice that we have Euler's Identity by letting , and
, and  ,
,
and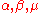 , and,
, and, 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:
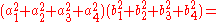
Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
wrote about this identity in a letter dated May 4, 1748 to Goldbach
Christian Goldbach
Christian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...
(but note that he used a different sign convention from the above). It can be proven with elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
and holds in every commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. If the
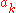 and
and  are real number
are real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, a more elegant proof is available: the identity expresses the fact that the absolute value of the product of two quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s is equal to the product of their absolute values, in the same way that the Brahmagupta-Fibonacci two-square identity
Brahmagupta-Fibonacci identity
In algebra, Brahmagupta's identity, also called Fibonacci's identity, implies that the product of two sums each of two squares is itself a sum of two squares. In other words, the set of all sums of two squares is closed under multiplication...
does for complex numbers.
The identity was used by Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
to prove his four square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
. More specifically, it implies that it is sufficient to prove the theorem for prime numbers, after which the more general theorem follows. The sign convention used above corresponds to the signs obtained by multiplying two quaternions. Other sign conventions can be obtained by changing any
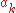 to
to 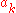 ,
, 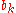 to
to 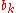 , or by changing the signs inside any of the squared terms on the right hand side.
, or by changing the signs inside any of the squared terms on the right hand side.However, a different kind of four-square identity can be given as,
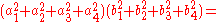
More generally, while Hurwitz's theorem states that an identity of form,
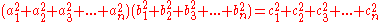
where the
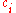 are bilinear
are bilinearBilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
functions of the
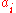 and
and  is possible only for n = {1, 2, 4, 8}, the more general Pfister's theorem allows that if the
is possible only for n = {1, 2, 4, 8}, the more general Pfister's theorem allows that if the  are just rational functions of one set of variables (in this case, the
are just rational functions of one set of variables (in this case, the 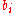 ), hence has a denominator, then it is possible for all
), hence has a denominator, then it is possible for all 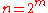 .
.- Euler's Four Square Identity can be further Generalized by letting
A,B, and C be the Coefficients of four Binary Quartic Forms,
whose Variables are
 , and
, and 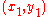
Also let
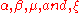 be any quantities desired. Then
be any quantities desired. ThenThe derivation of this is done in pure algebra.
The algebra needed to derive this Identity can be found in a PDF file called the
Generalization of Euler's Four Squares (about 60 pages ). It can be found at http://www.samz.us
Notice that we have Euler's Identity by letting
 , and
, and  ,
,and
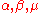 , and,
, and, 
External links
- A Collection of Algebraic Identities
- http://math.dartmouth.edu/~euler/correspondence/letters/OO0841.pdf Lettre CXV from Euler to Goldbach