
Essential dimension
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, essential dimension is an invariant defined for certain algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s such as algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s and quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s. It was introduced by J. Buhler and Z. Reichstein
Zinovy Reichstein
Zinovy Reichstein is a Russian-born American mathematician. He is a professor at the University of British Columbia in Vancouver.He studies mainly algebra, algebraic geometry and algebraic groups. He introduced the concept of essential dimension.Reichstein received his PhD degree in 1988 from...
and in its most generality defined by A. Merkurjev
Alexander Merkurjev
Alexander Merkurjev is a Russian-born American mathematician, who has made major contributions to the field of algebra. Currently Merkurjev is a professor at the University of California, Los Angeles.-Awards and distinctions:...
.
Basically, essential dimension measures the complexity of algebraic structures via their field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s of definition. For example, a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
q : V → K over a field K, where V is a K-vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, is said to be defined over a subfield L of K if there exists a K-basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
e1,...,en of V such that q can be expressed in the form
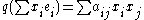 with all coefficients aij belonging to L.
with all coefficients aij belonging to L.

