Equivariant cohomology
Encyclopedia
In mathematics
, equivariant cohomology is a theory from algebraic topology
which applies to spaces with a group
action
. It can be viewed as a common generalization of group cohomology
and an ordinary cohomology theory.
Specifically, given a group
(discrete or not), a topological space
and an action
equivariant cohomology determines a graded ring
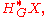
the equivariant cohomology ring. If
is the trivial group
, this is just the ordinary cohomology ring
of
, whereas if 
is contractible, it reduces to the group cohomology of 
.
and 
, called the homotopy orbit space
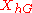of 
on
. (The 'h' distinguishes it from the ordinary orbit space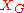 
.)
If
is the trivial group this space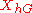 
will turn out to be just 
itself, whereas if 
is contractible the space will be a classifying space
for
.
by its 
-action) in which 
is first replaced by a larger but homotopy equivalent space so that the action is guaranteed to be free
.
To this end, construct the universal bundle
for 
and recall that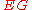 
has a free 
-action. Then the product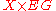 
—which is homotopy equivalent to 
since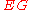 
is contractible—has a “diagonal” 
-action defined by taking the 
-action on each factor: moreover, this action is free since it is free on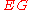 
. So we define the homotopy orbit space to be the orbit space of this 
-action.
This construction is denoted by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, equivariant cohomology is a theory from algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
which applies to spaces with a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. It can be viewed as a common generalization of group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
and an ordinary cohomology theory.
Specifically, given a group
(discrete or not), a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and an actionequivariant cohomology determines a graded ring
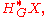
the equivariant cohomology ring. If
is the trivial groupTrivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, this is just the ordinary cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
of
, whereas if is contractible, it reduces to the group cohomology of .Outline construction
Equivariant cohomology can be constructed as the ordinary cohomology of a suitable space determined by and , called the homotopy orbit space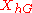 of on
. (The 'h' distinguishes it from the ordinary orbit space 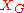.)If
is the trivial group this space 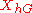will turn out to be just itself, whereas if is contractible the space will be a classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for
.Properties of the homotopy orbit space
- If
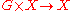is a free action then 
- If
is a trivial action then 
- In particular (as a special case of either of the above) if
is trivial then 
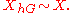
Construction of the homotopy orbit space
The homotopy orbit space is a “homotopically correct” version of the orbit space (the quotient of by its -action) in which is first replaced by a larger but homotopy equivalent space so that the action is guaranteed to be freeGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
.
To this end, construct the universal bundle
Universal bundle
In mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group G, is a specific bundle over a classifying space BG, such that every bundle with the given structure group G over M is a pullback by means of a continuous map-In the CW complex...
for and recall that 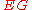has a free -action. Then the product 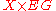—which is homotopy equivalent to since 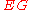is contractible—has a “diagonal” -action defined by taking the -action on each factor: moreover, this action is free since it is free on 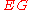. So we define the homotopy orbit space to be the orbit space of this -action.This construction is denoted by
Further reading
- Equivariant cohomology and equivariant intersection theory http://www-fourier.ujf-grenoble.fr/~mbrion/notesmontreal.pdf, Michel Brion