In logic

Logic

In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...

 and philosophy

Philosophy

Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...

, S5 is one of five systems of modal logic

Modal logic

Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...

 proposed by
Clarence Irving Lewis

Clarence Irving Lewis

Clarence Irving Lewis , usually cited as C. I. Lewis, was an American academic philosopher and the founder of conceptual pragmatism. First a noted logician, he later branched into epistemology, and during the last 20 years of his life, he wrote much on ethics.-Early years:Lewis was born in...

 and Cooper Harold Langford in their 1932 book Symbolic Logic.
It is a normal modal logic

Normal modal logic

In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...

, and one of the oldest systems of modal logic of any kind.

Axiomatics

S5 is characterized by the axioms:

• K: ;
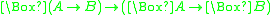• T: ,

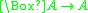and either:

• 5: ;
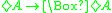• or both of the following:
• 4: 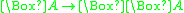, and
• B: .

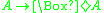Kripke semantics

In terms of Kripke semantics

Kripke semantics

Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...

, S5 is characterized by models where the accessibility relation is an equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

: it is reflexive

Reflexive relation

In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...

, transitive

Transitive relation

In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....

, and symmetric

Symmetric relation

In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...

. Alternatively, S5 can be characterized by models where the accessibility relation is "universal", that is, every world is accessible from any other. Although these characterizations produce different sets of models (since the former, but not the latter, allows for "closed" systems of worlds such that no world in one is accessible from any world in the other), they both model the theorems of S5.

Determining the satisfiability of an S5 formula is an NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

 problem. The hardness proof is trivial, as S5 includes the propositional logic. Membership is proved by showing that any satisfiable formula has a Kripke model where the number of worlds is at most linear in the size of the formula.

Applications

S5 is useful because it avoids superfluous iteration of qualifiers of different kinds. For example, under S5, if X is necessarily, possibly, necessarily possible, then X is possible. The unbolded qualifiers are superfluous under S5. Only the final "possible" is important. While this is useful for keeping propositions reasonably short, it also might appear counter-intuitive in that, under S5, if something is possibly necessary, then it is necessary - i.e. what is possibly necessary is necessary in at least one possible world, hence it is necessary in all possible worlds and thus is true in all possible worlds. This reasoning underpins at least one of the 'modal' formulations of the ontological argument

Ontological argument

The ontological argument for the existence of God is an a priori argument for the existence of God. The ontological argument was first proposed by the eleventh-century monk Anselm of Canterbury, who defined God as the greatest possible being we can conceive...

 for the existence of God - see Axiom S5

Axiom S5

Axiom S5 is the distinctive axiom of the S5 modal logic and states that if possibly p, then necessarily possibly p. It also states, perhaps less intuitively and more controversially, that if possibly necessarily p, then necessarily p...

.

External links

• http://home.utah.edu/~nahaj/logic/structures/systems/s5.html
• http://www.columbia.edu/~av72/modallogic/LectureNotes/ModalLogic06.pdf