
Entropy power inequality
Encyclopedia
In mathematics
, the entropy power inequality is a result in probability theory
that relates to so-called "entropy power" of random variable
s. It shows that the entropy power of suitably well-behaved
random variables is a superadditive function
. The entropy power inequality was proved in 1948 by Claude Shannon in his seminal paper "A Mathematical Theory of Communication
". Shannon also provided a sufficient condition for equality to hold; Stam (1959) showed that the condition is in fact necessary.
f : Rn → R, the differential entropy
of X, denoted h(X), is defined to be
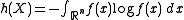
and the entropy power of X, denoted N(X), is defined to be

In particular,N(X) = |K| 1/n when X ~ ΦK.
Let X and Y be independent random variables with probability density functions in the Lp space
Lp(Rn) for some p > 1. Then
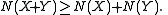
Moreover, equality holds if and only if
X and Y are multivariate normal random variables with proportional covariance matrices
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the entropy power inequality is a result in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
that relates to so-called "entropy power" of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. It shows that the entropy power of suitably well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
random variables is a superadditive function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. The entropy power inequality was proved in 1948 by Claude Shannon in his seminal paper "A Mathematical Theory of Communication
A Mathematical Theory of Communication
"A Mathematical Theory of Communication" is an influential 1948 article by mathematician Claude E. Shannon. As of November 2011, Google Scholar has listed more than 48,000 unique citations of the article and the later-published book version...
". Shannon also provided a sufficient condition for equality to hold; Stam (1959) showed that the condition is in fact necessary.
Statement of the inequality
For a random variable X : Ω → Rn with probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f : Rn → R, the differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
of X, denoted h(X), is defined to be
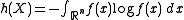
and the entropy power of X, denoted N(X), is defined to be

In particular,N(X) = |K| 1/n when X ~ ΦK.
Let X and Y be independent random variables with probability density functions in the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
Lp(Rn) for some p > 1. Then
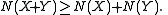
Moreover, equality holds if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
X and Y are multivariate normal random variables with proportional covariance matrices
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
.

