
Effective diffusion coefficient
Encyclopedia
The effective diffusion coefficient (also referred to as the apparent diffusion coefficient) of a diffusant in atomic diffusion
of solid polycrystalline
materials like metal alloys is often represented as a weighted average of the grain boundary diffusion coefficient
and the lattice diffusion coefficient
. Diffusion along both the grain boundary and in the lattice may be modeled with an Arrhenius equation
. The ratio of the grain boundary diffusion activation energy over the lattice diffusion activation energy is usually 0.4 - 0.6, so as temperature is lowered, the grain boundary diffusion component increases. Increasing temperature often allows for increased grain size, and the lattice diffusion component increases with increasing temperature, so often at 0.8Tmelt (of an alloy), the grain boundary component can be neglected.
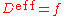 Dgb
Dgb 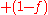 Dl.
Dl.
where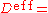 effective diffusion coefficient.
effective diffusion coefficient.
Grain boundary diffusion is significant in face centered cubic metals below about 0.8 Tmelt (Absolute). Line dislocations and other crystalline defects
can become significant below ~0.4 Tmelt in FCC metals.
Atomic diffusion
Atomic diffusion is a diffusion process whereby the random thermally-activated movement of atoms in a solid results in the net transport of atoms. For example, helium atoms inside a balloon can diffuse through the wall of the balloon and escape, resulting in the balloon slowly deflating. Other air...
of solid polycrystalline
Polycrystalline
Polycrystalline materials are solids that are composed of many crystallites of varying size and orientation. The variation in direction can be random or directed, possibly due to growth and processing conditions. Fiber texture is an example of the latter.Almost all common metals, and many ceramics...
materials like metal alloys is often represented as a weighted average of the grain boundary diffusion coefficient
Grain boundary diffusion coefficient
The grain boundary diffusion coefficient is the diffusion coefficient of a diffusant along a grain boundary in a polycrystalline solid. At lower temperatures in metals and metal alloys, this diffusion term may dominate the effective diffusion rate.- See also :* Kirkendall effect* Phase...
and the lattice diffusion coefficient
Lattice diffusion coefficient
Lattice diffusion refers to atomic diffusion within a crystalline lattice . Diffusion within the crystal lattice occurs by either interstitial or substitutional mechanisms and is referred to as lattice diffusion...
. Diffusion along both the grain boundary and in the lattice may be modeled with an Arrhenius equation
Arrhenius equation
The Arrhenius equation is a simple, but remarkably accurate, formula for the temperature dependence of the reaction rate constant, and therefore, rate of a chemical reaction. The equation was first proposed by the Dutch chemist J. H. van 't Hoff in 1884; five years later in 1889, the Swedish...
. The ratio of the grain boundary diffusion activation energy over the lattice diffusion activation energy is usually 0.4 - 0.6, so as temperature is lowered, the grain boundary diffusion component increases. Increasing temperature often allows for increased grain size, and the lattice diffusion component increases with increasing temperature, so often at 0.8Tmelt (of an alloy), the grain boundary component can be neglected.
Modeling
The effective diffusion coefficient can be modeled using Hart's equation when only grain boundary and lattice diffusion are dominant: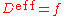 Dgb
Dgb 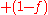 Dl.
Dl.where
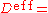 effective diffusion coefficient.
effective diffusion coefficient.
- Dgb = grain boundary diffusion coefficient.
- Dl = lattice diffusion coefficient.
 .δ
.δ value based on grain shape, 1 for parallel grains, 3 for square grains.
value based on grain shape, 1 for parallel grains, 3 for square grains. average grain size.
average grain size. - δ
 grain boundary width,often assumed to be 0.5 nm.
grain boundary width,often assumed to be 0.5 nm.
Grain boundary diffusion is significant in face centered cubic metals below about 0.8 Tmelt (Absolute). Line dislocations and other crystalline defects
Crystallographic defect
Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
can become significant below ~0.4 Tmelt in FCC metals.

