
Eddington luminosity
Encyclopedia
The Eddington luminosity (also referred to as the Eddington limit) in a star is defined as the point where the gravitational force inwards equals the continuum radiation force outwards, assuming hydrostatic equilibrium
and spherical symmetry. When exceeding the Eddington luminosity, a star would initiate a very intense continuum-driven stellar wind
from its outer layers. Since most massive stars have luminosities far below the Eddington luminosity, however, their winds are mostly driven by the less intense line absorption.
Originally, Sir Arthur Stanley Eddington
took only the electron scattering into account when calculating this limit, something that now is called the classical Eddington limit. Nowadays, the modified Eddington limit also counts on other continuum processes such as bound-free and free-free
interaction.
The pressure support of a star is given by the equation of hydrostatic equilibrium
:
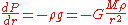
The outward force of radiation pressure is given by:

where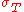 is the Thomson scattering
is the Thomson scattering
cross-section for the electron
and the gas is assumed to be purely made of ionized hydrogen. is the opacity of the stellar material.
is the opacity of the stellar material.
Equating these two pressures and solving for the luminosity gives the Eddington Luminosity:
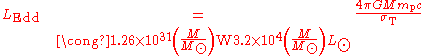
where is the mass of the central object,
is the mass of the central object,  ☉ the mass of the Sun
☉ the mass of the Sun
and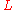 ☉ the luminosity of the Sun
☉ the luminosity of the Sun
, the mass of a proton and
the mass of a proton and  the Thomson cross-section for the electron.
the Thomson cross-section for the electron.
The mass of the proton appears because, in the typical environment for the outer layers of a star, the radiation pressure acts on electrons, which are driven away from the center. Because protons are negligibly pressured by the analog of Thomson scattering, due to their larger mass, the result is to create a slight charge separation and therefore a radially directed electric field, acting to lift the positive charges, which are typically free protons under the conditions in stellar atmospheres. When the outward electric field is sufficient to levitate the protons against gravity, both electrons and protons are expelled together.
plasma
. In other circumstances the pressure balance can be different than it is for hydrogen.
In an evolved star with a pure helium
atmosphere, the electric field would have to lift a helium nucleus (an alpha particle
), with nearly 4 times the mass of a proton, while the radiation pressure would act on 2 free electrons. Thus twice the usual Eddington luminosity would be needed to drive off an atmosphere of pure helium.
At very high temperatures, as in the environment of a black hole
or neutron star
, high energy photon interactions with nuclei or even with other photons, can create an electron-positron plasma. In that situation the mass of the neutralizing positive charge carriers is nearly 1836 times smaller (the proton to electron mass ratio), while the radiation pressure on the positrons doubles the effective upward force per unit mass, so the limiting luminosity needed is reduced by a factor of ≈1836/2=918.
The exact value of the Eddington luminosity depends on the chemical composition of the gas layer and the spectral energy distribution of the emission. Gas with cosmological abundances of hydrogen and helium is much more transparent than gas with solar abundance ratios. Atomic line transitions can greatly increase the effects of radiation pressure, and line driven winds exist in some bright stars.
Gamma-ray bursts, novae
and supernovae
are examples of systems exceeding their Eddington luminosity by a large factor for very short times, resulting in short and highly intensive mass loss rates. Some X-ray binaries and active galaxies are able to maintain luminosities close to the Eddington limit for very long times. For accretion powered sources such as accreting neutron star
s or cataclysmic variables (accreting white dwarfs), the limit may act to reduce or cut off the accretion flow, imposing an Eddington limit on accretion corresponding to that on luminosity. Super-Eddington accretion onto stellar-mass black holes is one possible model for ultraluminous X-ray sources (ULXs).
For accreting black hole
s, all the energy released by accretion does not have to appear as outgoing luminosity, since energy can be lost through the event horizon
, down the hole. Such sources effectively may not conserve energy. Then the accretion efficiency, or the fraction of energy actually radiated of that theoretically available from the gravitational energy release of accreting material, enters in an essential way.
Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
and spherical symmetry. When exceeding the Eddington luminosity, a star would initiate a very intense continuum-driven stellar wind
Stellar wind
A stellar wind is a flow of neutral or charged gas ejected from the upper atmosphere of a star. It is distinguished from the bipolar outflows characteristic of young stars by being less collimated, although stellar winds are not generally spherically symmetric.Different types of stars have...
from its outer layers. Since most massive stars have luminosities far below the Eddington luminosity, however, their winds are mostly driven by the less intense line absorption.
Originally, Sir Arthur Stanley Eddington
Arthur Stanley Eddington
Sir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
took only the electron scattering into account when calculating this limit, something that now is called the classical Eddington limit. Nowadays, the modified Eddington limit also counts on other continuum processes such as bound-free and free-free
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
interaction.
Derivation
The limit is obtained by setting the outward continuum radiation pressure equal to the inward gravitational force. Both forces decrease by inverse square laws, so once equality is reached, the hydrodynamic flow is different throughout the star.The pressure support of a star is given by the equation of hydrostatic equilibrium
Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
:
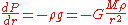
The outward force of radiation pressure is given by:

where
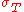 is the Thomson scattering
is the Thomson scatteringThomson scattering
Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is just the low-energy limit of Compton scattering: the particle kinetic energy and photon frequency are the same before and after the scattering...
cross-section for the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and the gas is assumed to be purely made of ionized hydrogen.
 is the opacity of the stellar material.
is the opacity of the stellar material.Equating these two pressures and solving for the luminosity gives the Eddington Luminosity:
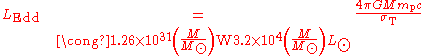
where
 is the mass of the central object,
is the mass of the central object,  ☉ the mass of the Sun
☉ the mass of the SunSun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
and
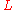 ☉ the luminosity of the Sun
☉ the luminosity of the SunSun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
,
 the mass of a proton and
the mass of a proton and  the Thomson cross-section for the electron.
the Thomson cross-section for the electron.The mass of the proton appears because, in the typical environment for the outer layers of a star, the radiation pressure acts on electrons, which are driven away from the center. Because protons are negligibly pressured by the analog of Thomson scattering, due to their larger mass, the result is to create a slight charge separation and therefore a radially directed electric field, acting to lift the positive charges, which are typically free protons under the conditions in stellar atmospheres. When the outward electric field is sufficient to levitate the protons against gravity, both electrons and protons are expelled together.
Different limits for different materials
The derivation above for the outward light pressure assumes a hydrogenHydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
. In other circumstances the pressure balance can be different than it is for hydrogen.
In an evolved star with a pure helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
atmosphere, the electric field would have to lift a helium nucleus (an alpha particle
Alpha particle
Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus, which is classically produced in the process of alpha decay, but may be produced also in other ways and given the same name...
), with nearly 4 times the mass of a proton, while the radiation pressure would act on 2 free electrons. Thus twice the usual Eddington luminosity would be needed to drive off an atmosphere of pure helium.
At very high temperatures, as in the environment of a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
or neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
, high energy photon interactions with nuclei or even with other photons, can create an electron-positron plasma. In that situation the mass of the neutralizing positive charge carriers is nearly 1836 times smaller (the proton to electron mass ratio), while the radiation pressure on the positrons doubles the effective upward force per unit mass, so the limiting luminosity needed is reduced by a factor of ≈1836/2=918.
The exact value of the Eddington luminosity depends on the chemical composition of the gas layer and the spectral energy distribution of the emission. Gas with cosmological abundances of hydrogen and helium is much more transparent than gas with solar abundance ratios. Atomic line transitions can greatly increase the effects of radiation pressure, and line driven winds exist in some bright stars.
Super-Eddington luminosities
The role of the Eddington limit in today’s research lies in explaining the very high mass loss rates seen in for example the series of outbursts of η Carinae in 1840–1860. The regular, line driven stellar winds can only stand for a mass loss rate of around 10−4–10−3 solar masses per year, whereas mass loss rates of up to 0.5 solar masses per year are needed to understand the η Carinae outbursts. This can be done with the help of the super-Eddington continuum driven winds.Gamma-ray bursts, novae
Nova
A nova is a cataclysmic nuclear explosion in a star caused by the accretion of hydrogen on to the surface of a white dwarf star, which ignites and starts nuclear fusion in a runaway manner...
and supernovae
Supernova
A supernova is a stellar explosion that is more energetic than a nova. It is pronounced with the plural supernovae or supernovas. Supernovae are extremely luminous and cause a burst of radiation that often briefly outshines an entire galaxy, before fading from view over several weeks or months...
are examples of systems exceeding their Eddington luminosity by a large factor for very short times, resulting in short and highly intensive mass loss rates. Some X-ray binaries and active galaxies are able to maintain luminosities close to the Eddington limit for very long times. For accretion powered sources such as accreting neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s or cataclysmic variables (accreting white dwarfs), the limit may act to reduce or cut off the accretion flow, imposing an Eddington limit on accretion corresponding to that on luminosity. Super-Eddington accretion onto stellar-mass black holes is one possible model for ultraluminous X-ray sources (ULXs).
For accreting black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s, all the energy released by accretion does not have to appear as outgoing luminosity, since energy can be lost through the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
, down the hole. Such sources effectively may not conserve energy. Then the accretion efficiency, or the fraction of energy actually radiated of that theoretically available from the gravitational energy release of accreting material, enters in an essential way.
Other factors
The Eddington limit is not a strict limit on the luminosity of a stellar object. The limit does not consider several potentially important factors, and super-Eddington objects have been observed that do not seem to have the predicted high mass-loss rate. Other factors that might affect the maximum luminosity of a star include:- Porosity. A problem with steady, continuum-driven winds is that both the radiative flux and gravitational acceleration scale with r−2. The ratio between these factors is constant, and in a super-Eddington star, the whole envelope would become gravitationally unbound at the same time. This is not observed. A possible solution is introducing an atmospheric porosity, where we imagine the stellar atmosphere to consist of denser regions surrounded by lower density gas regions. This would reduce the coupling between radiation and matter, and the full force of the radiation field would only be seen in the more homogeneous outer, lower density layers of the atmosphere.
- Turbulence. A possible destabilizing factor might be the turbulent pressure arising when energy in the convection zoneConvection zoneThe convection zone of a star is the range of radii in which energy is transported primarily by convection. In the radiation zone, energy is transported by radiation...
s builds up a field of supersonic turbulence. The importance of turbulence is being debated, however.
- Photon bubbles. Another factor that might explain some stable super-Eddington objects is the photon bubblePhoton bubbleA photon bubble is a type of radiation-driven instability that can occur in the magnetized, radiation-supported gas surrounding neutron stars, black hole accretion disks or at the edge of ultra-compact HII regions around young, massive stars. The instability occurs as follows...
effect. Photon bubbles would develop spontaneously in radiation-dominated atmospheres when the magnetic pressure exceeds the gas pressure. We can imagine a region in the stellar atmosphere with a density lower than the surroundings, but with a higher radiation pressure. Such a region would rise through the atmosphere, with radiation diffusing in from the sides, leading to an even higher radiation pressure. This effect could transport radiation more efficiently than a homogeneous atmosphere, increasing the allowed total radiation rate. In accretion discAccretion discAn accretion disc is a structure formed by diffuse material in orbital motion around a central body. The central body is typically a star. Gravity causes material in the disc to spiral inward towards the central body. Gravitational forces compress the material causing the emission of...
s, luminosities may be as high as 10–100 times the Eddington limit without experiencing instabilities.

