
Dynamo theory
Encyclopedia
In geophysics
, dynamo theory proposes a mechanism by which a celestial body such as the Earth
or a star
generates a magnetic field
. The theory describes the process through which a rotating, convecting
, and electrically conducting fluid can maintain a magnetic field over astronomical time scales.
. In 1919, Joseph Larmor
proposed that a dynamo might be generating the field. However, even after he advanced his theory, some prominent scientists advanced alternate theories. Einstein, believed that there might be an asymmetry between the charges of the electron
and proton
so that the Earth's magnetic field
would be produced by the entire Earth. The Nobel Prize
winner Patrick Blackett did a series of experiments looking for a fundamental relation between angular momentum
and magnetic moment
, but found none.
Walter M. Elsasser
, considered a "father" of the presently accepted dynamo theory as an explanation of the Earth's magnetism, proposed that this magnetic field resulted from electric currents induced in the fluid outer core of the Earth. He revealed the history of the Earth's magnetic field through pioneering the study of the magnetic orientation of minerals in rocks.
In order to maintain the magnetic field against ohm
ic decay (which would occur for the dipole field in 20,000 years) the outer core must be convecting. The convection is likely some combination of thermal and compositional convection
. The mantle controls the rate at which heat is extracted from the core. Heat sources include gravitational energy released by the compression of the core, gravitational energy released by the rejection of light elements (probably sulfur
, oxygen
, or silicon
) at the inner core boundary as it grows, latent heat of crystallization at the inner core boundary, and radioactivity of potassium
, uranium
and thorium
.
At the dawn of the 21st century, numerical modeling of the Earth's magnetic field has not been successfully demonstrated, but appears to be in reach. Initial models are focused on field generation by convection in the planet's fluid outer core. It was possible to show the generation of a strong, Earth-like field when the model assumed a uniform core-surface temperature and exceptionally high viscosities for the core fluid. Computations which incorporated more realistic parameter values yielded magnetic fields that were less Earth-like, but also point the way to model refinements which may ultimately lead to an accurate analytic model. Slight variations in the core-surface temperature, in the range of a few millikelvins, result in significant increases in convective flow and produce more realistic magnetic fields.
is ionized gas at the tachocline
. Dynamo theory of astrophysical bodies uses magnetohydrodynamic
equations to investigate how the fluid can continuously regenerate the magnetic field.
It was actually once believed that the dipole
, which comprises much of the Earth's magnetic field
and is misaligned along the rotation axis by 11.3 degrees, was caused by permanent magnetization of the materials in the earth. This means that dynamo theory was originally used to explain the Sun's magnetic field in its relationship with that of the Earth. However, this theory, which was initially proposed by Joseph Larmor
in 1919, has been modified due to extensive studies of magnetic secular variation, paleomagnetism
(including polarity reversal
s), seismology, and the solar system's abundance of elements. Also, the application of the theories of Carl Friedrich Gauss
to magnetic observations showed that Earth's magnetic field had an internal, rather than external, origin.
There are three requisites for a dynamo to operate:
In the case of the Earth, the magnetic field is induced and constantly maintained by the convection of liquid iron in the outer core. A requirement for the induction of field is a rotating fluid. Rotation in the outer core is supplied by the Coriolis effect
caused by the rotation of the Earth. The coriolis force tends to organize fluid motions and electric currents into columns (also see Taylor column
s) aligned with the rotation axis. Induction or creation of magnetic field is described by the induction equation:
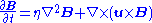
where u is velocity, B is magnetic field, t is time, and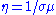 is the magnetic diffusivity with
is the magnetic diffusivity with  electrical conductivity and
electrical conductivity and 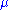 permeability
permeability
. The ratio of the second term on the right hand side to the first term gives the Magnetic Reynolds number
, a dimensionless ratio of advection of magnetic field to diffusion.
Using Maxwell's equations
simultaneously with the curl of Ohm's Law
, one can derive what is basically the linear eigenvalue equation for magnetic fields (B) which can be done when assuming that the magnetic field is independent from the velocity field. One arrives at a critical magnetic Reynolds number above which the flow strength is sufficient to amplify the imposed magnetic field, and below which it decays.
The most functional feature of kinematic dynamo theory is that it can be used to test whether a velocity field is or is not capable of dynamo action. By applying a certain velocity field to a small magnetic field, it can be determined through observation whether the magnetic field tends to grow or not in reaction to the applied flow. If the magnetic field does grow, then the system is either capable of dynamo action or is a dynamo, but if the magnetic field does not grow, then it is simply referred to as non-dynamo.
The membrane paradigm
is a way of looking at black hole
s that allows for the material near their surfaces to be expressed in the language of dynamo theory.
, and so the induction equation is no longer linear in the magnetic field. In most cases this leads to a quenching of the amplitude of the dynamo. Such dynamos are sometimes also referred to as
hydromagnetic dynamos.
Virtually all dynamos in astrophysics and geophysics are hydromagnetic dynamos.
Numerical models are used to simulate fully nonlinear dynamos. A minimum of 5 equations are needed. They are as follows. The induction equation, see above. Maxwell's equation:

The (sometimes) Boussinesq
conservation of mass:
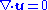
The (sometimes) Boussinesq conservation of momentum, also known as the Navier-Stokes equation:
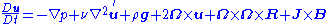
where is the kinematic viscosity
is the kinematic viscosity
,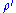 is the density perturbation that provides buoyancy (for thermal convection
is the density perturbation that provides buoyancy (for thermal convection 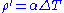 ,
,  is the rotation rate of the Earth, and
is the rotation rate of the Earth, and 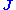 is the electrical current density.
is the electrical current density.
Finally, a transport equation, usually of heat (sometimes of light element concentration):
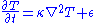
where T is temperature, is the thermal diffusivity with k thermal conductivity,
is the thermal diffusivity with k thermal conductivity, 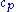 heat capacity, and
heat capacity, and  density, and
density, and  is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed. These equations are then non-dimensionalized, introducing the non-dimensional parameters,
is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed. These equations are then non-dimensionalized, introducing the non-dimensional parameters,
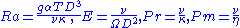
where Ra is the Rayleigh number
, E the Ekman number
, Pr and Pm the Prandtl and magnetic Prandtl number. Magnetic field scaling is often in Elsasser number units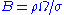 .
.
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
, dynamo theory proposes a mechanism by which a celestial body such as the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
or a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
generates a magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. The theory describes the process through which a rotating, convecting
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
, and electrically conducting fluid can maintain a magnetic field over astronomical time scales.
History of theory
When William Gilbert published de Magnete in 1600, he concluded that the Earth is magnetic and proposed the first theory for the origin of this magnetism: permanent magnetism such as that found in lodestoneLodestone
A lodestone or loadstone is a naturally magnetized piece of the mineral magnetite. They are naturally occurring magnets, that attract pieces of iron. Ancient people first discovered the property of magnetism in lodestone...
. In 1919, Joseph Larmor
Joseph Larmor
Sir Joseph Larmor , a physicist and mathematician who made innovations in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter...
proposed that a dynamo might be generating the field. However, even after he advanced his theory, some prominent scientists advanced alternate theories. Einstein, believed that there might be an asymmetry between the charges of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
so that the Earth's magnetic field
Earth's magnetic field
Earth's magnetic field is the magnetic field that extends from the Earth's inner core to where it meets the solar wind, a stream of energetic particles emanating from the Sun...
would be produced by the entire Earth. The Nobel Prize
Nobel Prize
The Nobel Prizes are annual international awards bestowed by Scandinavian committees in recognition of cultural and scientific advances. The will of the Swedish chemist Alfred Nobel, the inventor of dynamite, established the prizes in 1895...
winner Patrick Blackett did a series of experiments looking for a fundamental relation between angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
, but found none.
Walter M. Elsasser
Walter M. Elsasser
Walter Maurice Elsasser was a German-born American physicist considered a "father" of the presently accepted dynamo theory as an explanation of the Earth's magnetism. He proposed that this magnetic field resulted from electric currents induced in the fluid outer core of the Earth...
, considered a "father" of the presently accepted dynamo theory as an explanation of the Earth's magnetism, proposed that this magnetic field resulted from electric currents induced in the fluid outer core of the Earth. He revealed the history of the Earth's magnetic field through pioneering the study of the magnetic orientation of minerals in rocks.
In order to maintain the magnetic field against ohm
Ohm
The ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,...
ic decay (which would occur for the dipole field in 20,000 years) the outer core must be convecting. The convection is likely some combination of thermal and compositional convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
. The mantle controls the rate at which heat is extracted from the core. Heat sources include gravitational energy released by the compression of the core, gravitational energy released by the rejection of light elements (probably sulfur
Sulfur
Sulfur or sulphur is the chemical element with atomic number 16. In the periodic table it is represented by the symbol S. It is an abundant, multivalent non-metal. Under normal conditions, sulfur atoms form cyclic octatomic molecules with chemical formula S8. Elemental sulfur is a bright yellow...
, oxygen
Oxygen
Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...
, or silicon
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
) at the inner core boundary as it grows, latent heat of crystallization at the inner core boundary, and radioactivity of potassium
Potassium
Potassium is the chemical element with the symbol K and atomic number 19. Elemental potassium is a soft silvery-white alkali metal that oxidizes rapidly in air and is very reactive with water, generating sufficient heat to ignite the hydrogen emitted in the reaction.Potassium and sodium are...
, uranium
Uranium
Uranium is a silvery-white metallic chemical element in the actinide series of the periodic table, with atomic number 92. It is assigned the chemical symbol U. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons...
and thorium
Thorium
Thorium is a natural radioactive chemical element with the symbol Th and atomic number 90. It was discovered in 1828 and named after Thor, the Norse god of thunder....
.
At the dawn of the 21st century, numerical modeling of the Earth's magnetic field has not been successfully demonstrated, but appears to be in reach. Initial models are focused on field generation by convection in the planet's fluid outer core. It was possible to show the generation of a strong, Earth-like field when the model assumed a uniform core-surface temperature and exceptionally high viscosities for the core fluid. Computations which incorporated more realistic parameter values yielded magnetic fields that were less Earth-like, but also point the way to model refinements which may ultimately lead to an accurate analytic model. Slight variations in the core-surface temperature, in the range of a few millikelvins, result in significant increases in convective flow and produce more realistic magnetic fields.
Formal definition
Dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid acts to maintain a magnetic field. This theory is used to explain the presence of anomalously long-lived magnetic fields in astrophysical bodies. The conductive fluid in the geodynamo is liquid iron in the outer core, and in the solar dynamoSolar dynamo
The solar dynamo is the physical process that generates the Sun's magnetic field. The Sun is permeated by an overall dipole magnetic field, as are many other celestial bodies such as the Earth. The dipole field is produced by a circular electric current flowing deep within the star, following...
is ionized gas at the tachocline
Tachocline
The tachocline is the transition region of the Sun between the radiative interior and the differentially rotating outer convective zone. It is in the outer third of the sun . This causes the region to have a very large shear as the rotation rate changes very rapidly...
. Dynamo theory of astrophysical bodies uses magnetohydrodynamic
Magnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
equations to investigate how the fluid can continuously regenerate the magnetic field.
It was actually once believed that the dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
, which comprises much of the Earth's magnetic field
Earth's magnetic field
Earth's magnetic field is the magnetic field that extends from the Earth's inner core to where it meets the solar wind, a stream of energetic particles emanating from the Sun...
and is misaligned along the rotation axis by 11.3 degrees, was caused by permanent magnetization of the materials in the earth. This means that dynamo theory was originally used to explain the Sun's magnetic field in its relationship with that of the Earth. However, this theory, which was initially proposed by Joseph Larmor
Joseph Larmor
Sir Joseph Larmor , a physicist and mathematician who made innovations in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter...
in 1919, has been modified due to extensive studies of magnetic secular variation, paleomagnetism
Paleomagnetism
Paleomagnetism is the study of the record of the Earth's magnetic field in rocks. Certain minerals in rocks lock-in a record of the direction and intensity of the magnetic field when they form. This record provides information on the past behavior of Earth's magnetic field and the past location of...
(including polarity reversal
Geomagnetic reversal
A geomagnetic reversal is a change in the Earth's magnetic field such that the positions of magnetic north and magnetic south are interchanged. The Earth's field has alternated between periods of normal polarity, in which the direction of the field was the same as the present direction, and reverse...
s), seismology, and the solar system's abundance of elements. Also, the application of the theories of Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
to magnetic observations showed that Earth's magnetic field had an internal, rather than external, origin.
There are three requisites for a dynamo to operate:
- An electrically conductive fluid medium
- Kinetic energy provided by planetary rotation
- An internal energy source to drive convective motions within the fluid.
In the case of the Earth, the magnetic field is induced and constantly maintained by the convection of liquid iron in the outer core. A requirement for the induction of field is a rotating fluid. Rotation in the outer core is supplied by the Coriolis effect
Coriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
caused by the rotation of the Earth. The coriolis force tends to organize fluid motions and electric currents into columns (also see Taylor column
Taylor column
A Taylor column is a feature of the coriolis effect. It was named after Geoffrey Ingram Taylor. Rotating fluids that are perturbed tend to form columns parallel to the axis of rotation called Taylor columns....
s) aligned with the rotation axis. Induction or creation of magnetic field is described by the induction equation:
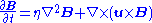
where u is velocity, B is magnetic field, t is time, and
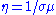 is the magnetic diffusivity with
is the magnetic diffusivity with  electrical conductivity and
electrical conductivity and 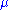 permeability
permeabilityPermeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
. The ratio of the second term on the right hand side to the first term gives the Magnetic Reynolds number
Magnetic Reynolds number
The Magnetic Reynolds number is a dimensionless group thatoccurs in magnetohydrodynamics. It gives an estimate of the effects of magnetic advection to magnetic diffusion, and is typically defined by:where* U is a typical velocity scale of the flow...
, a dimensionless ratio of advection of magnetic field to diffusion.
Kinematic dynamo theory
In kinematic dynamo theory the velocity field is prescribed, instead of being a dynamic variable. This method cannot provide the time variable behavior of a fully nonlinear chaotic dynamo but is useful in studying how magnetic field strength varies with the flow structure and speed.Using Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
simultaneously with the curl of Ohm's Law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
, one can derive what is basically the linear eigenvalue equation for magnetic fields (B) which can be done when assuming that the magnetic field is independent from the velocity field. One arrives at a critical magnetic Reynolds number above which the flow strength is sufficient to amplify the imposed magnetic field, and below which it decays.
The most functional feature of kinematic dynamo theory is that it can be used to test whether a velocity field is or is not capable of dynamo action. By applying a certain velocity field to a small magnetic field, it can be determined through observation whether the magnetic field tends to grow or not in reaction to the applied flow. If the magnetic field does grow, then the system is either capable of dynamo action or is a dynamo, but if the magnetic field does not grow, then it is simply referred to as non-dynamo.
The membrane paradigm
Membrane paradigm
In black hole theory, the black hole membrane paradigm is a useful "toy model" method or "engineering approach" for visualising and calculating the effects predicted by quantum mechanics for the exterior physics of black holes, without using quantum-mechanical principles or calculations...
is a way of looking at black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s that allows for the material near their surfaces to be expressed in the language of dynamo theory.
Nonlinear dynamo theory
The kinematic approximation becomes invalid when the magnetic field becomes strong enough to affect the fluid motions. In that case the velocity field becomes affected by the Lorentz forceLorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, and so the induction equation is no longer linear in the magnetic field. In most cases this leads to a quenching of the amplitude of the dynamo. Such dynamos are sometimes also referred to as
hydromagnetic dynamos.
Virtually all dynamos in astrophysics and geophysics are hydromagnetic dynamos.
Numerical models are used to simulate fully nonlinear dynamos. A minimum of 5 equations are needed. They are as follows. The induction equation, see above. Maxwell's equation:

The (sometimes) Boussinesq
Boussinesq approximation
In fluid dynamics, the Boussinesq approximation is used in the field of buoyancy-driven flow . It states that density differences are sufficiently small to be neglected, except where they appear in terms multiplied by g, the acceleration due to gravity...
conservation of mass:
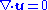
The (sometimes) Boussinesq conservation of momentum, also known as the Navier-Stokes equation:
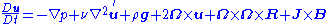
where
 is the kinematic viscosity
is the kinematic viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
,
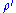 is the density perturbation that provides buoyancy (for thermal convection
is the density perturbation that provides buoyancy (for thermal convection 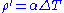 ,
,  is the rotation rate of the Earth, and
is the rotation rate of the Earth, and 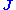 is the electrical current density.
is the electrical current density.Finally, a transport equation, usually of heat (sometimes of light element concentration):
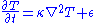
where T is temperature,
 is the thermal diffusivity with k thermal conductivity,
is the thermal diffusivity with k thermal conductivity, 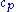 heat capacity, and
heat capacity, and  density, and
density, and  is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed. These equations are then non-dimensionalized, introducing the non-dimensional parameters,
is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed. These equations are then non-dimensionalized, introducing the non-dimensional parameters,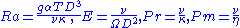
where Ra is the Rayleigh number
Rayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
, E the Ekman number
Ekman number
The Ekman number is a dimensionless number used in describing geophysical phenomena in the oceans and atmosphere. It characterises the ratio of viscous forces in a fluid to the fictitious forces arising from planetary rotation...
, Pr and Pm the Prandtl and magnetic Prandtl number. Magnetic field scaling is often in Elsasser number units
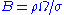 .
.See also
- Antidynamo theoremAntidynamo theoremIn physics and in particular in the theory of magnetism, an antidynamo theorem is one of several results that restrict the type of magnetic fields that may be produced by dynamo action....
- DynamoDynamo- Engineering :* Dynamo, a magnetic device originally used as an electric generator* Dynamo theory, a theory relating to magnetic fields of celestial bodies* Solar dynamo, the physical process that generates the Sun's magnetic field- Software :...
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Rotating magnetic fieldRotating magnetic fieldA rotating magnetic field is a magnetic field which changes direction at a constant angular rate. This is a key principle in the operation of the alternating-current motor. Nikola Tesla claimed in his autobiography that he identified the concept of the rotating magnetic field in 1882. In 1885,...

