Distributed constraint optimization
Encyclopedia
Distributed constraint optimization (DCOP or DisCOP) is the distributed
analogue to constraint optimization
. A DCOP is a problem in which a group of agents must distributedly choose values for a set of variables such that the cost
of a set of constraints over the variables is either minimized or maximized.
Distributed Constraint Satisfaction is a framework for describing a problem in terms of constraints that are known and enforced by distinct participants (agents). The constraints are described on some variables with predefined domains, and have to be assigned to the same values by the different agents.
Problems defined with this framework can be solved by any of the algorithms that are proposed for it.
The framework was used under different names in the 1980s. The first known usage with the current name is in 1990.
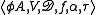, where:
The objective of a DCOP is to have each agent assign values to its associated variables in order to either minimize or maximize
for a given assignment of the variables.
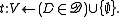
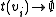implies that the agent 
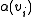has not yet assigned a value to variable 
. Given this representation, the "domain
" (i.e., the set of input values) of the function
function) as an input to the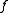 
function.
problem is as follows: given a graph
and a set of colors 
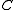, assign each vertex
,
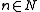, a color, 
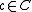, such that the number of adjacent vertices with the same color is minimized.
As a DCOP, there is one agent per vertex that is assigned to decide the associated color. Each agent has a single variable whose associated domain is of cardinality
(there is one domain value for each possible color). For each vertex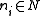 
, create a variable in the DCOP 
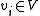with domain 
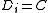. For each pair of adjacent vertices 
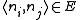, create a constraint of cost 1 if both of the associated variables are assigned the same color: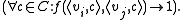 
.
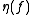is as follows: given a set of items of varying volume and a set of knapsacks of varying capacity, assign each item to a knapsack such that the amount of overflow is minimized. Let
be the set of items,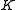 
be the set of knapsacks, 
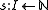be a function mapping items to their volume, and 
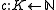be a function mapping knapsacks to their capacities.
To encode this problem as a DCOP, for each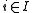
create one variable 
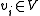with associated domain 
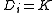. Then for all possible context 
:
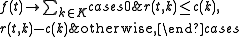
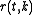is a function such that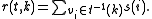
ADOPT, for example, uses best-first search, asynchronous synchronization, point-to-point communication between neighboring agents in the constraint graph and a constraint tree as main communication topology.
Hybrids of these DCOP algorithms also exist. BnB-Adopt, for example, changes the search strategy of Adopt from best-first search to depth-first branch-and-bound search.
See Chapters 1 and 2; downloadable free online.
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
analogue to constraint optimization
Constraint optimization
In constraint satisfaction, constrained optimization seeks for a solution maximizing or minimizing a cost function.-Definition:...
. A DCOP is a problem in which a group of agents must distributedly choose values for a set of variables such that the cost
of a set of constraints over the variables is either minimized or maximized.
Distributed Constraint Satisfaction is a framework for describing a problem in terms of constraints that are known and enforced by distinct participants (agents). The constraints are described on some variables with predefined domains, and have to be assigned to the same values by the different agents.
Problems defined with this framework can be solved by any of the algorithms that are proposed for it.
The framework was used under different names in the 1980s. The first known usage with the current name is in 1990.
DCOP
A DCOP can be defined as a tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
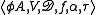, where:
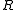is a set of agentsIntelligent agentIn artificial intelligence, an intelligent agent is an autonomous entity which observes through sensors and acts upon an environment using actuators and directs its activity towards achieving goals . Intelligent agents may also learn or use knowledge to achieve their goals...
;
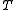is a set of variables, 
;
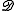is a set of domains, 
, where each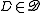 
is a finite set containing the values to which its associated variable may be assigned;
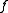is function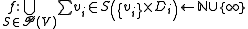
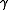is a function 
mapping variables to their associated agent.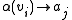 
implies that it is agent 
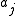's responsibility to assign the value of variable 
. Note that it is not necessarily true that 
is either an injectionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
or surjection; and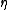
is an operator that aggregates all of the individual 
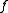costs for all possible variable assignments. This is usually accomplished through summation:
.
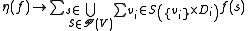The objective of a DCOP is to have each agent assign values to its associated variables in order to either minimize or maximize
for a given assignment of the variables.Context
A Context is a variable assignment for a DCOP. This can be thought of as a function mapping variables in the DCOP to their current values: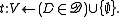 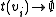implies that the agent 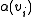has not yet assigned a value to variable . Given this representation, the "domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
" (i.e., the set of input values) of the function
f can be thought of as the set of all possible contexts for the DCOP. Therefore, in the remainder of this article we may use the notion of a context (i.e., the function) as an input to the 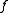function.Distributed graph coloring
The graph coloringGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
problem is as follows: given a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
and a set of colors 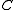, assign each vertexVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
,
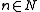, a color, 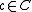, such that the number of adjacent vertices with the same color is minimized.As a DCOP, there is one agent per vertex that is assigned to decide the associated color. Each agent has a single variable whose associated domain is of cardinality
(there is one domain value for each possible color). For each vertex 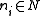, create a variable in the DCOP 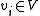with domain 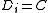. For each pair of adjacent vertices 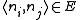, create a constraint of cost 1 if both of the associated variables are assigned the same color: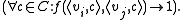 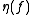.Distributed multiple knapsack problem
The distributed multiple- variant of the knapsack problemKnapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
is as follows: given a set of items of varying volume and a set of knapsacks of varying capacity, assign each item to a knapsack such that the amount of overflow is minimized. Let
be the set of items, 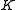be the set of knapsacks, 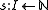be a function mapping items to their volume, and 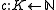be a function mapping knapsacks to their capacities.To encode this problem as a DCOP, for each
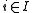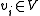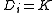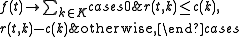
create one variable with associated domain . Then for all possible context : 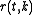is a function such that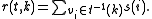Algorithms
DCOP algorithms can be classified according to the search strategy (best-first search or depth-first branch-and-bound search), the synchronization among agents (synchronous or asynchronous), the communication among agents (point-to-point with neighbors in the constraint graph or broadcast) and the main communication topology (chain or tree).ADOPT, for example, uses best-first search, asynchronous synchronization, point-to-point communication between neighboring agents in the constraint graph and a constraint tree as main communication topology.
| Algorithm Name | Year Introduced | Memory Complexity Computational complexity theory Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other... |
Number of Messages | Correctness Correctness In theoretical computer science, correctness of an algorithm is asserted when it is said that the algorithm is correct with respect to a specification... / Completeness Completeness In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems... |
Implementations |
|---|---|---|---|---|---|
| NCBB No-Commitment Branch and Bound |
2006 | Polynomial (or any-space) | Exponential | Proven | Reference Implementation: not publicly released DCOPolis (GNU LGPL GNU Lesser General Public License The GNU Lesser General Public License or LGPL is a free software license published by the Free Software Foundation . It was designed as a compromise between the strong-copyleft GNU General Public License or GPL and permissive licenses such as the BSD licenses and the MIT License... ) |
| DPOP Distributed Pseudotree Optimization Procedure |
2005 | Exponential | Linear | Proven | Reference Implementation: FRODO (GNU Affero GPL Affero General Public License The Affero General Public License, often abbreviated as Affero GPL and AGPL , refers to two distinct, though historically related, free software licenses:... ) DCOPolis (GNU LGPL GNU Lesser General Public License The GNU Lesser General Public License or LGPL is a free software license published by the Free Software Foundation . It was designed as a compromise between the strong-copyleft GNU General Public License or GPL and permissive licenses such as the BSD licenses and the MIT License... ) |
| OptAPO Asynchronous Partial Overlay |
2004 | Polynomial | Exponential | Proven, but proof of completeness has been challenged | Reference Implementation: OptAPO DCOPolis (GNU LGPL GNU Lesser General Public License The GNU Lesser General Public License or LGPL is a free software license published by the Free Software Foundation . It was designed as a compromise between the strong-copyleft GNU General Public License or GPL and permissive licenses such as the BSD licenses and the MIT License... ); In Development |
| Adopt Asynchronous Backtracking |
2003 | Polynomial (or any-space) | Exponential | Proven | Reference Implementation: Adopt DCOPolis (GNU LGPL GNU Lesser General Public License The GNU Lesser General Public License or LGPL is a free software license published by the Free Software Foundation . It was designed as a compromise between the strong-copyleft GNU General Public License or GPL and permissive licenses such as the BSD licenses and the MIT License... ) FRODO (GNU Affero GPL Affero General Public License The Affero General Public License, often abbreviated as Affero GPL and AGPL , refers to two distinct, though historically related, free software licenses:... ) |
| Secure Multiparty Computation For Solving DisCSPs (MPC-DisCSP1-MPC-DisCSP4) |
2003 | Note: secure if 1/2 of the participants are trustworthy | |||
| Secure Computation with Semi-Trusted Servers | 2002 | Note: security increases with the number of trustworthy servers | |||
| ABTR Asynchronous Backtracking with Reordering |
2001 | Note: eordering in ABT with bounded nogoods | |||
| DMAC Maintaining Asynchronously Consistencies |
2001 | Note: the fastest algorithm | |||
| AAS Asynchronous Aggregation Search |
2000 | aggregation of values in ABT | |||
| DFC Distributed Forward Chaining |
2000 | Note: low, comparable to ABT | |||
| DBA Distributed Breakout Algorithm |
1995 | Note: incomplete but fast | FRODO version 1 | ||
| AWC Asynchronous Weak-Commitment |
1994 | Note: reordering, fast, complete (only with exponential space) | |||
| ABT Asynchronous Backtracking |
1992 | Note: static ordering, complete | |||
Hybrids of these DCOP algorithms also exist. BnB-Adopt, for example, changes the search strategy of Adopt from best-first search to depth-first branch-and-bound search.
Books and Surveys
A chapter in an edited book.See Chapters 1 and 2; downloadable free online.
- Yokoo, M., and Hirayama, K. (2000). Algorithms for distributed constraint satisfaction: A review. Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems (pp. 185–207). A survey.