
Distance correlation
Encyclopedia
In statistics
and in probability theory
, distance correlation is a measure of statistical dependence between two random variable
s or two random vectors of arbitrary, not necessarily equal dimension. Its important property is that this measure of dependence is zero if and only if the random variables
are statistically independent. This measure is derived from a number of other quantities that are used in its specification, specifically: distance variance, distance standard deviation and distance covariance. These take the same roles as the ordinary moment
s with corresponding names in the specification of the Pearson product-moment correlation coefficient
.
These distance-based measures can be put into an indirect relationship to the ordinary moments by an alternative formulation (described below) using ideas related to Brownian motion
, and this has led to the use of names such as Brownian covariance and Brownian distance covariance.
, is mainly sensitive to a linear relationship between two variables. Distance correlation was introduced in 2005 by Gabor J Szekely in several lectures to address this deficiency of Pearson’s correlation
, namely that it can easily be zero for dependent variables. Correlation = 0 (uncorrelatedness) does not imply independence while distance correlation = 0 does imply independence. The first results on distance correlation were published in 2007 and 2009. It was proved that distance covariance is the same as the Brownian covariance. These measures are examples of energy distance
s.
where E denotes expected value, |.| denotes Euclidean norm, and (X,Y), (X',Y'), and (X",Y") are independent and identically distributed. Distance covariance can be expressed in terms of Pearson’s covariance, cov, as follows: dCov2(X,Y) = cov(|X–X'|, |Y–Y'|) – 2cov(|X–X'|, |Y–Y"|). This identity shows that the distance covariance is not the same as the covariance of distances, cov(|X–X'|, |Y–Y'|), which can be zero even if X and Y are not independent.
The sample distance covariance is defined as follows. Let (Xk Yk), k=1,2,…, n be a statistical sample from a pair of real valued or vector valued random variables (X,Y). First, compute all pairwise distances
That is, compute the n by n distance matrices (ak,l) and (bk,l). Then take all centered distances Ak,l:= ak,l –k.–.l + .. and Bk,l:= bk,l – k. - .l + .. where k. is the k-th row mean, .l is the l-th column mean, and .. is the grand mean of the distance matrix of the X sample. The notation is similar for the b values. (In the matrices of centered distances (Ak,l) and (Bk,l) all row sums and all column sums equal zero.) The squared sample distance covariance is simply the arithmetic average of the products Ak,l Bk,l; that is
The statistic Tn = n[dcov2n (X,Y)] determines a consistent multivariate test of independence of random vectors in arbitrary dimensions. For an implementation see dcov.test function in the energy package for R
.
The population value of distance variance is the square root of
where E denotes the expected value, X’ is an independent and identically distributed copy of X and X" is independent of X and X' and has the same distribution as X and X'.
The sample distance variance is the square root of
which is a relative of Corrado Gini
’s mean difference
introduced in 1912 (but Gini did not work with centered distances).

and the sample distance correlation is defined by substituting the sample distance covariance and distance variances for the population coefficients above.
For easy computation of sample distance correlation see the dcor function in the energy package for R
.
(ii) dCor(X,Y) = 0 if and only if X and Y are independent.
(iii) dcorn(X,Y) = 1 implies that dimensions of the linear spaces spanned by X and Y samples respectively are almost surely equal and if we assume that these subspaces are equal, then in this subspace Y = a + b CX for some vector a, scalar b, and orthonormal matrix C.
(ii) dCov2(a1 +b1 C1 X, a2 +b2 C2 Y) = |b1 b2| dCov2(X,Y)
for all constant vectors a1, a2 , scalars b1, b2, and orthonormal matrices C1, C2.
(iii) If the random vectors (X1, Y1) and (X2, Y2) are independent then
Equality holds if and only if X1 and Y1 are both constants, or X2 and Y2 are both constants, or X1, X2, Y1, Y2 are mutually independent.
(iv) dCov (X,Y) = 0 if and only if X and Y are independent.
This last property is the most important effect of working with centered distances.
The statistic dcov2n (X,Y) is a biased estimator of dCov2(X,Y) because E[dcov2n (X,Y)] = [(n-1)/n2][(n-2)dCov2(X,Y)+E|X-X’|E|Y-Y’|]. The bias therefore can easily be corrected.
(ii) dVarn (X) = 0 if and only if every sample observation is identical.
(iii) dVar(a + bCX) = |b| dVar(X) for all constant vectors a, scalars b, and orthonormal matrices C.
(iv) If X and Y are independent then dVar(X + Y) ≤ dVar(X) + dVar(Y).
Equality holds if (iv) if and only if one of the random variables X or Y is a constant.
Then for every 0 < α < 2, X and Y are independent if and only if dCov2(X, Y; α) = 0. It is important to note that this characterization does not hold for exponent α = 2; in this case for bivariate (X, Y), dCor(X, Y; α=2) is a deterministic function of the Pearson correlation. If ak,l and bk,l are α powers of the corresponding distances, 0 < α ≤ 2, then α sample distance covariance can be defined as the nonnegative number for which
One can extend dCov to metric space
valued random variables X and Y: ak,l = K(Xk, Xl) and bk,l = L(Yk, Yl) where K, L are squares of metrics and (strictly) negative definite continuous functions.
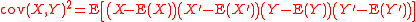
where E denotes the expected value
and the prime denotes independent and identically distributed copies. We need the following generalization of this formula. If U(s), V(t) are arbitrary random processes defined for all real s and t then define the U-centered version of X by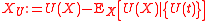
whenever the subtracted conditional expected value exists and denote by YV the V-centered version of Y. The (U,V) covariance of (X,Y) is defined as the nonnegative number whose square is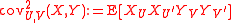
whenever the right-hand side is nonnegative and finite. The most important example is when U and V are two-sided independent Brownian motion
s /Wiener process
es with expectation zero and covariance
|s| + |t| - |s-t| = 2 min(s,t). (This is twice the covariance of the standard Wiener process; here the factor 2 simplifies the computations.) In this case the (U,V) covariance is called Brownian covariance and is denoted by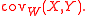
There is a surprising coincidence: The Brownian covariance is the same as the distance covariance:
On the other hand, if we replace the Brownian motion with the deterministic identity function id then Covid(X,Y) is simply the absolute value of the classical Pearson covariance
,
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, distance correlation is a measure of statistical dependence between two random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s or two random vectors of arbitrary, not necessarily equal dimension. Its important property is that this measure of dependence is zero if and only if the random variables
Multivariate random variable
In mathematics, probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.More formally, a multivariate random...
are statistically independent. This measure is derived from a number of other quantities that are used in its specification, specifically: distance variance, distance standard deviation and distance covariance. These take the same roles as the ordinary moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s with corresponding names in the specification of the Pearson product-moment correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
.
These distance-based measures can be put into an indirect relationship to the ordinary moments by an alternative formulation (described below) using ideas related to Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, and this has led to the use of names such as Brownian covariance and Brownian distance covariance.
Background
The classical measure of dependence, the Pearson correlation coefficientPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
, is mainly sensitive to a linear relationship between two variables. Distance correlation was introduced in 2005 by Gabor J Szekely in several lectures to address this deficiency of Pearson’s correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, namely that it can easily be zero for dependent variables. Correlation = 0 (uncorrelatedness) does not imply independence while distance correlation = 0 does imply independence. The first results on distance correlation were published in 2007 and 2009. It was proved that distance covariance is the same as the Brownian covariance. These measures are examples of energy distance
Energy distance
Energy distance is a statistical distance between probability distributions. If X and Y are independent random vectors in Rd, with cumulative distribution functions F and G respectively, then the energy distance between the distributions F and G is definedwhere X, X' are independent and identically...
s.
Distance covariance
The population value of distance covariance is the square root of- dCov2(X,Y):= E|X – X'||Y – Y'| + E|X – X'| E|Y – Y'| – E|X – X'||Y – Y"| - E|X – X"||Y – Y'|
-
-
- = E|X – X'||Y – Y'| + E|X – X'| E|Y – Y'| – 2E|X – X'||Y – Y"|,
-
-
where E denotes expected value, |.| denotes Euclidean norm, and (X,Y), (X',Y'), and (X",Y") are independent and identically distributed. Distance covariance can be expressed in terms of Pearson’s covariance, cov, as follows: dCov2(X,Y) = cov(|X–X'|, |Y–Y'|) – 2cov(|X–X'|, |Y–Y"|). This identity shows that the distance covariance is not the same as the covariance of distances, cov(|X–X'|, |Y–Y'|), which can be zero even if X and Y are not independent.
The sample distance covariance is defined as follows. Let (Xk Yk), k=1,2,…, n be a statistical sample from a pair of real valued or vector valued random variables (X,Y). First, compute all pairwise distances
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
- ak,l = |Xk – Xl | and bk,l = |Yk – Yl | for k,l=1,2,…,n.
That is, compute the n by n distance matrices (ak,l) and (bk,l). Then take all centered distances Ak,l:= ak,l –k.–.l + .. and Bk,l:= bk,l – k. - .l + .. where k. is the k-th row mean, .l is the l-th column mean, and .. is the grand mean of the distance matrix of the X sample. The notation is similar for the b values. (In the matrices of centered distances (Ak,l) and (Bk,l) all row sums and all column sums equal zero.) The squared sample distance covariance is simply the arithmetic average of the products Ak,l Bk,l; that is
- dcov2n (X,Y):= (1/n2) Σ k,l Ak,l Bk,l.
The statistic Tn = n[dcov2n (X,Y)] determines a consistent multivariate test of independence of random vectors in arbitrary dimensions. For an implementation see dcov.test function in the energy package for R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
.
Distance variance
The distance variance is a special case of distance covariance when the two variables are identical.The population value of distance variance is the square root of
- dVar2(X):= E|X – X'|2 + E2|X – X'| – 2E|X – X'||X – X"|,
where E denotes the expected value, X’ is an independent and identically distributed copy of X and X" is independent of X and X' and has the same distribution as X and X'.
The sample distance variance is the square root of
- dvar2n (X):=dcov2n (X,X) = (1/n2) Σ k,l A k,l2,
which is a relative of Corrado Gini
Corrado Gini
Corrado Gini was an Italian statistician, demographer and sociologist who developed the Gini coefficient, a measure of the income inequality in a society. Gini was also a leading fascist theorist and ideologue who wrote The Scientific Basis of Fascism in 1927...
’s mean difference
Mean difference
The mean difference is a measure of statistical dispersion equal to the average absolute difference of two independent values drawn from a probability distribution. A related statistic is the relative mean difference, which is the mean difference divided by the arithmetic mean...
introduced in 1912 (but Gini did not work with centered distances).
Distance standard deviation
The distance standard deviation is the square root of the distance variance.Distance correlation
The distance correlation of two random variables is obtained by dividing their distance covariance by the product of their distance standard deviations. The distance correlation is
and the sample distance correlation is defined by substituting the sample distance covariance and distance variances for the population coefficients above.
For easy computation of sample distance correlation see the dcor function in the energy package for R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
.
Distance correlation
(i) 0 ≤ dcorn(X,Y) ≤ 1 and 0 ≤ dCor(X,Y) ≤1.(ii) dCor(X,Y) = 0 if and only if X and Y are independent.
(iii) dcorn(X,Y) = 1 implies that dimensions of the linear spaces spanned by X and Y samples respectively are almost surely equal and if we assume that these subspaces are equal, then in this subspace Y = a + b CX for some vector a, scalar b, and orthonormal matrix C.
Distance covariance
(i) dCov (X,Y) ≥ 0 and dcovn (X,Y) ≥ 0.(ii) dCov2(a1 +b1 C1 X, a2 +b2 C2 Y) = |b1 b2| dCov2(X,Y)
for all constant vectors a1, a2 , scalars b1, b2, and orthonormal matrices C1, C2.
(iii) If the random vectors (X1, Y1) and (X2, Y2) are independent then
- dCov(X1 +X2, Y1 +Y2) ≤ dCov(X1, Y1) + dCov (X2, Y2).
Equality holds if and only if X1 and Y1 are both constants, or X2 and Y2 are both constants, or X1, X2, Y1, Y2 are mutually independent.
(iv) dCov (X,Y) = 0 if and only if X and Y are independent.
This last property is the most important effect of working with centered distances.
The statistic dcov2n (X,Y) is a biased estimator of dCov2(X,Y) because E[dcov2n (X,Y)] = [(n-1)/n2][(n-2)dCov2(X,Y)+E|X-X’|E|Y-Y’|]. The bias therefore can easily be corrected.
Distance variance
(i) dVar(X) = 0 if and only if X = E(X) almost surely.(ii) dVarn (X) = 0 if and only if every sample observation is identical.
(iii) dVar(a + bCX) = |b| dVar(X) for all constant vectors a, scalars b, and orthonormal matrices C.
(iv) If X and Y are independent then dVar(X + Y) ≤ dVar(X) + dVar(Y).
Equality holds if (iv) if and only if one of the random variables X or Y is a constant.
Generalization
Distance covariance can be generalized to include powers of Euclidean distance. Define- dCov2(X, Y; α):= E|X – X’|α|Y – Y’|α + E|X – X’|α E|Y – Y’|α – 2 E|X – X’|α|Y – Y"|α.
Then for every 0 < α < 2, X and Y are independent if and only if dCov2(X, Y; α) = 0. It is important to note that this characterization does not hold for exponent α = 2; in this case for bivariate (X, Y), dCor(X, Y; α=2) is a deterministic function of the Pearson correlation. If ak,l and bk,l are α powers of the corresponding distances, 0 < α ≤ 2, then α sample distance covariance can be defined as the nonnegative number for which
- dcov2n (X,Y ; α):= (1/n2) Σ k,lAk,l Bk,l.
One can extend dCov to metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
valued random variables X and Y: ak,l = K(Xk, Xl) and bk,l = L(Yk, Yl) where K, L are squares of metrics and (strictly) negative definite continuous functions.
Alternative formulation: Brownian covariance
Brownian covariance is motivated by generalization of the notion of covariance to stochastic processes. The square of the covariance of random variables X and Y can be written in the following form: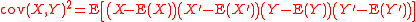
where E denotes the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and the prime denotes independent and identically distributed copies. We need the following generalization of this formula. If U(s), V(t) are arbitrary random processes defined for all real s and t then define the U-centered version of X by
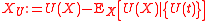
whenever the subtracted conditional expected value exists and denote by YV the V-centered version of Y. The (U,V) covariance of (X,Y) is defined as the nonnegative number whose square is
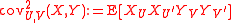
whenever the right-hand side is nonnegative and finite. The most important example is when U and V are two-sided independent Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
s /Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
es with expectation zero and covariance
|s| + |t| - |s-t| = 2 min(s,t). (This is twice the covariance of the standard Wiener process; here the factor 2 simplifies the computations.) In this case the (U,V) covariance is called Brownian covariance and is denoted by
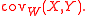
There is a surprising coincidence: The Brownian covariance is the same as the distance covariance:

On the other hand, if we replace the Brownian motion with the deterministic identity function id then Covid(X,Y) is simply the absolute value of the classical Pearson covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
,

See also
- RV coefficientRV coefficientIn statistics, the RV coefficientis a multivariate generalization of the Pearson correlation coefficient.It measures the closeness of two set of points that may each be represented in a matrix....
- For a related third-order statistic, see Distance skewness.

