
Descartes' rule of signs
Encyclopedia
In mathematics
, Descartes' rule of signs, first described by René Descartes
in his work La Géométrie
, is a technique for determining the number of positive or negative real roots of a polynomial
.
The rule gives us an upper bound number of positive or negative roots of a polynomial. It is not a complete criterion, i.e. it does not tell the exact number of positive or negative roots.
with real
coefficient
s are ordered by descending variable exponent, then the number of positive roots of the polynomial is either equal to the number of sign differences between consecutive nonzero coefficients, or is less than it by a multiple of 2. Multiple roots of the same value are counted separately.
of the rule, the number of negative roots is the number of sign changes after multiplying the coefficients of odd-power terms by −1, or fewer than it by a multiple of 2. This procedure is equivalent to substituting the negation of the variable for the variable itself: For example, to find the number of negative roots of , we equivalently ask how many positive roots there are for
, we equivalently ask how many positive roots there are for  in
in  Using Descartes' rule of signs on
Using Descartes' rule of signs on 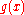 gives the number of positive roots
gives the number of positive roots 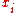 of g, and since
of g, and since 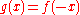 it gives the number of positive roots
it gives the number of positive roots 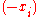 of f, which is the same as the number of negative roots
of f, which is the same as the number of negative roots 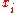 of f.
of f.

has one sign change between the second and third terms (the sequence of pairs of successive signs is ++, +−, −−). Therefore it has exactly one positive root. Note that the leading sign needs to be considered although in this particular example it does not affect the answer.
To find the number of negative roots, change the signs of the coefficients of the terms with odd exponents, to obtain a second polynomial

This polynomial has two sign changes (the sequence of pairs of successive signs is −+, ++, +−), meaning that this second polynomial has two or zero positive roots; thus the original polynomial has two or zero negative roots.
In fact, the factorization of the first polynomial is
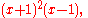
so the roots are −1 (twice) and 1.
The factorization of the second polynomial is
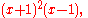
So here, the roots are 1 (twice) and −1, the negation of the roots of the original polynomial.
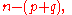
where p denotes the maximum number of positive roots, q denotes the maximum number of negative roots (both of which can be found using Descartes' rule of signs), and n denotes the degree of the equation. A simple example is the polynomial

If , this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients multiplied by −1. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is
, this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients multiplied by −1. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is 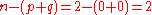 .
.
In the 1970s Askold Georgevich Khovanskiǐ developed the theory of fewnomials that generalises Descartes' rule. The rule of signs can be thought of as stating that the number of real roots of a polynomial is dependent on the polynomial's complexity, and that this complexity is proportional to the number of monomials it has, not its degree. Khovanskiǐ showed that this holds true not just for polynomials but for algebraic combinations of many transcendental functions, the so-called Pfaffian function
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Descartes' rule of signs, first described by René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
in his work La Géométrie
La Géométrie
La Géométrie was published in 1637 as an appendix to Discours de la méthode , written by René Descartes. In the Discourse, he presents his method for obtaining clarity on any subject...
, is a technique for determining the number of positive or negative real roots of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
.
The rule gives us an upper bound number of positive or negative roots of a polynomial. It is not a complete criterion, i.e. it does not tell the exact number of positive or negative roots.
Positive roots
The rule states that if the terms of a single-variable polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s are ordered by descending variable exponent, then the number of positive roots of the polynomial is either equal to the number of sign differences between consecutive nonzero coefficients, or is less than it by a multiple of 2. Multiple roots of the same value are counted separately.
Negative roots
As a corollaryCorollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of the rule, the number of negative roots is the number of sign changes after multiplying the coefficients of odd-power terms by −1, or fewer than it by a multiple of 2. This procedure is equivalent to substituting the negation of the variable for the variable itself: For example, to find the number of negative roots of
 , we equivalently ask how many positive roots there are for
, we equivalently ask how many positive roots there are for  in
in  Using Descartes' rule of signs on
Using Descartes' rule of signs on 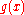 gives the number of positive roots
gives the number of positive roots 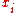 of g, and since
of g, and since 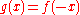 it gives the number of positive roots
it gives the number of positive roots 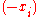 of f, which is the same as the number of negative roots
of f, which is the same as the number of negative roots 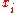 of f.
of f.Example
The polynomial
has one sign change between the second and third terms (the sequence of pairs of successive signs is ++, +−, −−). Therefore it has exactly one positive root. Note that the leading sign needs to be considered although in this particular example it does not affect the answer.
To find the number of negative roots, change the signs of the coefficients of the terms with odd exponents, to obtain a second polynomial

This polynomial has two sign changes (the sequence of pairs of successive signs is −+, ++, +−), meaning that this second polynomial has two or zero positive roots; thus the original polynomial has two or zero negative roots.
In fact, the factorization of the first polynomial is
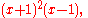
so the roots are −1 (twice) and 1.
The factorization of the second polynomial is
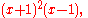
So here, the roots are 1 (twice) and −1, the negation of the roots of the original polynomial.
Complex roots
Since any nth degree polynomial has exactly n roots, the minimum number of complex roots is equal to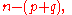
where p denotes the maximum number of positive roots, q denotes the maximum number of negative roots (both of which can be found using Descartes' rule of signs), and n denotes the degree of the equation. A simple example is the polynomial

If
 , this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients multiplied by −1. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is
, this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients multiplied by −1. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is 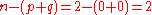 .
.Special case
The exclusion of multiples of 2 is because the polynomial may have complex roots which always come in pairs. Thus if the polynomial is known to have all real roots, this rule allows one to find the exact number of positive and negative roots. Since it is easy to determine the multiplicity of zero as a root, the sign of all roots can be determined in this case.Generalizations
If the real polynomial P has k real positive roots counted with multiplicity, then for every a > 0 there are at least k changes of sign in the sequence of coefficients of the Taylor series of the function eaxP(x).In the 1970s Askold Georgevich Khovanskiǐ developed the theory of fewnomials that generalises Descartes' rule. The rule of signs can be thought of as stating that the number of real roots of a polynomial is dependent on the polynomial's complexity, and that this complexity is proportional to the number of monomials it has, not its degree. Khovanskiǐ showed that this holds true not just for polynomials but for algebraic combinations of many transcendental functions, the so-called Pfaffian function
Pfaffian function
In mathematics, the Pfaffian functions are a certain class of functions introduced by Askold Georgevich Khovanskiǐ in the 1970s. They are named after German mathematician Johann Pfaff.-Basic definition:...
s.
See also
- Sturm's theoremSturm's theoremIn mathematics, Sturm's theorem is a symbolic procedure to determine the number of distinct real roots of a polynomial. It was named for Jacques Charles François Sturm...
- Rational root theorem
- Polynomial function theorems for zerosPolynomial function theorems for zerosPolynomial function theorems for zeros are a set of theorems aiming to find of the complex zeros of a polynomial function.Found in most precalculus textbooks, these theorems include:* Remainder theorem* Factor theorem...
- Properties of polynomial roots
- Gauss–Lucas theorem
External links
- Descartes’ Rule of Signs — Proof of the Rule

