Depth-slope product
Encyclopedia
The depth–slope product is used to calculate the shear stress
at the bed of an open channel
containing fluid
that is undergoing steady, uniform flow. It is widely used in river engineering
, stream restoration
, sedimentology
, and fluvial geomorphology. It is the product
of the water depth and the mean bed slope
, along with the acceleration due to gravity
and density
of the fluid.
channels: that the angle of the channel from horizontal is small enough that it can be approximated as the slope by the small-angle formula, and that the channel is much wider than it is deep, and sidewall effects can be ignored. Although it is a simplistic approach to find the shear stress in what can often be a locally unsteady fluvial
system, when averaged over distances of kilometers, these local variations average and the depth–slope product becomes a useful tool to understand shear stress in open channels such as rivers.
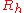, can be assumed to be equal to the channel depth, 
.
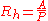
where
is the cross sectional area of flow and 
is wetted perimeter
. For a semicircular channel, the hydraulic radius would simply be the true radius
.
For an approximately rectangular channel (for simplicity in the mathematics of the explanation of the assumption),
,
where
is the width (breadth) of the channel, and
.
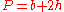For b>>h,
,
and therefore
.
Formally, this assumption can generally be held to hold when the width is greater than about 20 times the height; the exact amount of error accrued can be found by comparing the height to the hydraulic radius. For channels with a lower width-to-depth ratio, a better solution can be found by using the hydraulic radius instead of the above simplification.
, an acceleration due to gravity
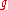, and a flow depth 
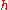, the pressure exerted on the bed is simply the weight of an element of fluid, 
, times the depth of the flow, 
. From this, we get the expression for the total pressure,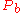 
, acting on the bed.
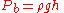
from horizontal, the shear component of the stress acting on the bed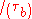 
, which is the component acting tangentially to the bed, equals the total pressure times the sine of the angle 
.
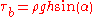
In natural rivers, the angle
is typically very small. As a result, the small-angle formula states that:
The tangent of the angle
is, by definition, equal to the slope
of the channel,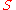
.
From this, we can arrive at the final form of the relation between bed shear stress and depth–slope product:
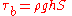
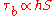
For natural streams, in the mks
or SI
system (units of pascals for shear stress), a typical useful relationship to remember is that:
for water with a density of 1000 kg/m3 and approximating the acceleration due to gravity as 10 m/s2 (the error in this assumption is typically much smaller than the error from measurements).
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
at the bed of an open channel
Open channel flow
Open-Channel Flow, a branch of Hydraulics, is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways, but differ in one important respect; the free surface...
containing fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
that is undergoing steady, uniform flow. It is widely used in river engineering
River engineering
River engineering is the process of planned human intervention in the course, characteristics or flow of a river with the intention of producing some defined benefit. People have intervened in the natural course and behaviour of rivers since before recorded history - to manage the water resources,...
, stream restoration
Stream restoration
Stream restoration or river restoration, sometimes called river reclamation in the UK, describes a set of activities that help improve the environmental health of a river or stream. Improved health may be indicated by expanded habitat for diverse species and reduced stream bank erosion...
, sedimentology
Sedimentology
Sedimentology encompasses the study of modern sediments such as sand, mud , and clay, and the processes that result in their deposition. Sedimentologists apply their understanding of modern processes to interpret geologic history through observations of sedimentary rocks and sedimentary...
, and fluvial geomorphology. It is the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of the water depth and the mean bed slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
, along with the acceleration due to gravity
Gravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
and density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the fluid.
Formulation
The use of the depth–slope product — in computing the bed shear-stress — specifically refers to two assumptions that are widely applicable to natural riverRiver
A river is a natural watercourse, usually freshwater, flowing towards an ocean, a lake, a sea, or another river. In a few cases, a river simply flows into the ground or dries up completely before reaching another body of water. Small rivers may also be called by several other names, including...
channels: that the angle of the channel from horizontal is small enough that it can be approximated as the slope by the small-angle formula, and that the channel is much wider than it is deep, and sidewall effects can be ignored. Although it is a simplistic approach to find the shear stress in what can often be a locally unsteady fluvial
Fluvial
Fluvial is used in geography and Earth science to refer to the processes associated with rivers and streams and the deposits and landforms created by them...
system, when averaged over distances of kilometers, these local variations average and the depth–slope product becomes a useful tool to understand shear stress in open channels such as rivers.
Depth and hydraulic radius
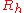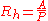
The first assumption is that the channel is much wider than it is deep, and the equations can be solved as if the channel were infinitely wide. This means that side-wall effects can be ignored, and that the hydraulic radius,, can be assumed to be equal to the channel depth, .where
is the cross sectional area of flow and is wetted perimeterWetted perimeter
The wetted perimeter is the perimeter of the cross sectional area that is "wet." The term wetted perimeter is common in Civil Engineering, Environmental Engineering and heat transfer applications; it is associated with the hydraulic diameter...
. For a semicircular channel, the hydraulic radius would simply be the true radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
.
For an approximately rectangular channel (for simplicity in the mathematics of the explanation of the assumption),
,where
is the width (breadth) of the channel, and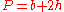.For b>>h,
,and therefore
.Formally, this assumption can generally be held to hold when the width is greater than about 20 times the height; the exact amount of error accrued can be found by comparing the height to the hydraulic radius. For channels with a lower width-to-depth ratio, a better solution can be found by using the hydraulic radius instead of the above simplification.
Pressure
The total stress on the bed of an open channel of infinite width is given by the hydrostatic pressure acting on the bed. For a fluid of densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, an acceleration due to gravityGravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
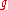, and a flow depth 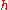, the pressure exerted on the bed is simply the weight of an element of fluid, , times the depth of the flow, . From this, we get the expression for the total pressure, 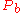, acting on the bed.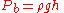Shear stress
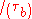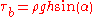
In order to convert the pressure into a shear stress, it is necessary to determine the component of the pressure that provides shear on the bed. For a channel that is at an angle from horizontal, the shear component of the stress acting on the bed , which is the component acting tangentially to the bed, equals the total pressure times the sine of the angle .In natural rivers, the angle
is typically very small. As a result, the small-angle formula states that:The tangent of the angle
is, by definition, equal to the slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the channel,
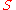.From this, we can arrive at the final form of the relation between bed shear stress and depth–slope product:
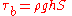
Scaling
Assuming a single, well-mixed, homogeneous fluid and a single acceleration due to gravity (both are good assumptions in natural rivers, and the second is a good assumption for processes on Earth, or any planetary body with a dominant influence on the local graviational field), the only two variables that determine the boundary shear stress are the depth and the slope. This is the significance of the name of the formula.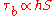For natural streams, in the mks
Mks system of units
The MKS system of units is a physical system of units that expresses any given measurement using fundamental units of the metre, kilogram, and/or second ....
or SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
system (units of pascals for shear stress), a typical useful relationship to remember is that:
for water with a density of 1000 kg/m3 and approximating the acceleration due to gravity as 10 m/s2 (the error in this assumption is typically much smaller than the error from measurements).
Uses
Bed shear stress can be used to find:- The vertical velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
profile within the fluid flow - The ability of the fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
to carry sedimentSediment transportSediment transport is the movement of solid particles , typically due to a combination of the force of gravity acting on the sediment, and/or the movement of the fluid in which the sediment is entrained... - The rate of shear dispersionDispersive mass transferDispersive mass transfer, in fluid dynamics, is the spreading of mass from highly concentrated areas to less concentrated areas. It is one form of mass transfer....
of contaminants and tracers.