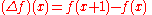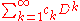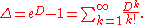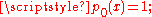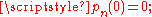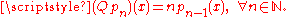Delta operator
Encyclopedia
In mathematics
, a delta operator is a shift-equivariant linear
operator on the vector space
on the vector space
of polynomial
s in a variable over a field
over a field
 that reduces degrees by one.
that reduces degrees by one.
To say that is shift-equivariant means that if
is shift-equivariant means that if 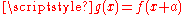 , then
, then

In other words, if is a "shift" of
is a "shift" of 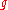 , then
, then  is also a shift of
is also a shift of 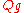 , and has the same "shifting vector"
, and has the same "shifting vector"  .
.
To say that an operator reduces degree by one means that if is a polynomial of degree
is a polynomial of degree  , then
, then  is either a polynomial of degree
is either a polynomial of degree  , or, in case
, or, in case  ,
,  is 0.
is 0.
Sometimes a delta operator is defined to be a shift-equivariant linear transformation on polynomials in that maps
that maps  to a nonzero constant. Seemingly weaker than the definition given above, this latter characterization can be shown to be equivalent to the stated definition, since shift-equivariance is a fairly strong condition.
to a nonzero constant. Seemingly weaker than the definition given above, this latter characterization can be shown to be equivalent to the stated definition, since shift-equivariance is a fairly strong condition.
 has a unique sequence of "basic polynomials", a polynomial sequence
has a unique sequence of "basic polynomials", a polynomial sequence
defined by three conditions:
Such a sequence of basic polynomials is always of binomial type, and it can be shown that no other sequences of binomial type exist. If the first two conditions above are dropped, then the third condition says this polynomial sequence is a Sheffer sequence -- a more general concept.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a delta operator is a shift-equivariant linear
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
operator
 on the vector space
on the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in a variable
 over a field
over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
 that reduces degrees by one.
that reduces degrees by one.To say that
 is shift-equivariant means that if
is shift-equivariant means that if 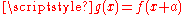 , then
, then
In other words, if
 is a "shift" of
is a "shift" of 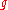 , then
, then  is also a shift of
is also a shift of 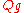 , and has the same "shifting vector"
, and has the same "shifting vector"  .
.To say that an operator reduces degree by one means that if
 is a polynomial of degree
is a polynomial of degree  , then
, then  is either a polynomial of degree
is either a polynomial of degree  , or, in case
, or, in case  ,
,  is 0.
is 0.Sometimes a delta operator is defined to be a shift-equivariant linear transformation on polynomials in
 that maps
that maps  to a nonzero constant. Seemingly weaker than the definition given above, this latter characterization can be shown to be equivalent to the stated definition, since shift-equivariance is a fairly strong condition.
to a nonzero constant. Seemingly weaker than the definition given above, this latter characterization can be shown to be equivalent to the stated definition, since shift-equivariance is a fairly strong condition.Examples
- The forward difference operator
- is a delta operator.
- DifferentiationDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
with respect to x, written as D, is also a delta operator.
- Any operator of the form
-
- (where Dn(ƒ) = ƒ(n) is the nth derivative) with
 is a delta operator. It can be shown that all delta operators can be written in this form. For example, the difference operator given above can be expanded as
is a delta operator. It can be shown that all delta operators can be written in this form. For example, the difference operator given above can be expanded as
- The generalized derivative of time scale calculusTime scale calculusIn mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
which unifies the forward difference operator with the derivative of standard calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
is a delta operator.
- In computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and cyberneticsCyberneticsCybernetics is the interdisciplinary study of the structure of regulatory systems. Cybernetics is closely related to information theory, control theory and systems theory, at least in its first-order form...
, the term "discrete-time delta operator" (δ) is generally taken to mean a difference operator
- the Euler approximation of the usual derivative with a discrete sample time
 . The delta-formulation obtains a significant number of numerical advantages compared to the shift-operator at fast sampling.
. The delta-formulation obtains a significant number of numerical advantages compared to the shift-operator at fast sampling.
Basic polynomials
Every delta operator has a unique sequence of "basic polynomials", a polynomial sequence
has a unique sequence of "basic polynomials", a polynomial sequencePolynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
defined by three conditions:
Such a sequence of basic polynomials is always of binomial type, and it can be shown that no other sequences of binomial type exist. If the first two conditions above are dropped, then the third condition says this polynomial sequence is a Sheffer sequence -- a more general concept.