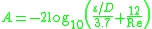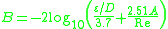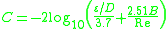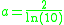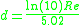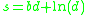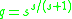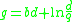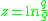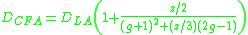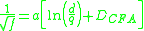Darcy friction factor formulae
Encyclopedia
In fluid dynamics
, the Darcy friction factor formulae are equations — based on experimental data and theory — for the Darcy friction factor. The Darcy friction factor is a dimensionless quantity
used in the Darcy–Weisbach equation, for the description of friction losses in pipe flow as well as open channel flow. It is also known as the Darcy–Weisbach friction factor or Moody friction factor and is four times larger than the Fanning friction factor.

where:
, Moody stated the accuracy is about ±5% for smooth pipes and ±10% for rough pipes. If more than one formula is applicable in the flow regime under consideration, the choice of formula may be influenced by one or more of the following:
. It was developed in 1939 by C. F. Colebrook. The 1937 paper by C. F. Colebrook and C. M. White is often erroneously cited as the source of the equation. This is partly because Colebrook in a footnote (from his 1939 paper) acknowledges his debt to White for suggesting the mathematical method by which the smooth and rough pipe correlations could be combined. The equation is used to iteratively solve for the Darcy–Weisbach friction factor f. This equation is also known as the Colebrook–White equation.
For conduits that are flowing completely full of fluid at Reynolds numbers greater than 4000, it is defined as:
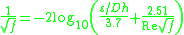
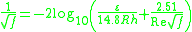
where:

and

Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Darcy friction factor formulae are equations — based on experimental data and theory — for the Darcy friction factor. The Darcy friction factor is a dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
used in the Darcy–Weisbach equation, for the description of friction losses in pipe flow as well as open channel flow. It is also known as the Darcy–Weisbach friction factor or Moody friction factor and is four times larger than the Fanning friction factor.
Flow regime
Which friction factor formula may be applicable depends upon the type of flow that exists:- Laminar flow
- Transition between laminar and turbulent flow
- Fully turbulent flow in smooth conduits
- Fully turbulent flow in rough conduits
- Free surface flow.
Laminar flow
The Darcy friction factor for laminar flow (Reynolds number less than 2000) is given by the following formula:
where:
-
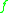 is the Darcy friction factor
is the Darcy friction factor -
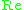 is the Reynolds number.
is the Reynolds number.
Transition flow
Transition (neither fully laminar nor fully turbulent) flow occurs in the range of Reynolds numbers between 2300 and 4000. The value of the Darcy friction factor may be subject to large uncertainties in this flow regime.Turbulent flow in smooth conduits
Empirical correlations exist for this flow regime. Such correlations are included in the ASHRAE Handbook of Fundamentals.Turbulent flow in rough conduits
The Darcy friction factor for fully turbulent flow (Reynolds number greater than 4000) in rough conduits is given by the Colebrook equation.Free surface flow
The last formula in the Colebrook equation section of this article is for free surface flow. The approximations elsewhere in this article are not applicable for this type of flow.Choosing a formula
Before choosing a formula it is worth knowing that in the paper on the Moody chartMoody chart
The Moody chart or Moody diagram is a graph in non-dimensional form that relates the Darcy friction factor, Reynolds number and relative roughness for fully developed flow in a circular pipe...
, Moody stated the accuracy is about ±5% for smooth pipes and ±10% for rough pipes. If more than one formula is applicable in the flow regime under consideration, the choice of formula may be influenced by one or more of the following:
- Required precision
- Speed of computation required
- Available computational technology:
- calculator (minimize keystrokes)
- spreadsheet (single-cell formula)
- programming/scripting language (subroutine).
Compact forms
The Colebrook equation is an implicit equation that combines experimental results of studies of turbulent flow in smooth and rough pipesPipe (material)
A pipe is a tubular section or hollow cylinder, usually but not necessarily of circular cross-section, used mainly to convey substances which can flow — liquids and gases , slurries, powders, masses of small solids...
. It was developed in 1939 by C. F. Colebrook. The 1937 paper by C. F. Colebrook and C. M. White is often erroneously cited as the source of the equation. This is partly because Colebrook in a footnote (from his 1939 paper) acknowledges his debt to White for suggesting the mathematical method by which the smooth and rough pipe correlations could be combined. The equation is used to iteratively solve for the Darcy–Weisbach friction factor f. This equation is also known as the Colebrook–White equation.
For conduits that are flowing completely full of fluid at Reynolds numbers greater than 4000, it is defined as:
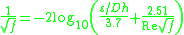
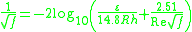
where:
-
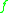 is the Darcy friction factor
is the Darcy friction factor - Roughness height,
 (m, ft)
(m, ft) - Hydraulic diameter,
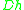 (m, ft) — For fluid-filled, circular conduits,
(m, ft) — For fluid-filled, circular conduits, 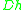 = D = inside diameter
= D = inside diameter - Hydraulic radius,
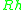 (m, ft) — For fluid-filled, circular conduits,
(m, ft) — For fluid-filled, circular conduits, 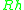 = D/4 = (inside diameter)/4
= D/4 = (inside diameter)/4 -
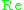 is the Reynolds number.
is the Reynolds number.
Solving
The Colebrook equation used to be solved numerically due to its apparent implicit nature. Recently, the Lambert W function has been employed to obtained explicit reformulation of the Colebrook equation.Expanded forms
Additional, mathematically equivalent forms of the Colebrook equation are:
-
- where:
- 1.7384... = 2 log (2 × 3.7) = 2 log (7.4)
- 18.574 = 2.51 × 3.7 × 2
- where:
and

- or
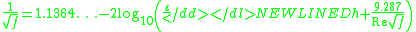
-
- where:
- 1.1364... = 1.7384... − 2 log (2) = 2 log (7.4) − 2 log (2) = 2 log (3.7)
- 9.287 = 18.574 / 2 = 2.51 × 3.7.
- where:
The additional equivalent forms above assume that the constants 3.7 and 2.51 in the formula at the top of this section are exact. The constants are probably values which were rounded by Colebrook during his curve fittingCurve fittingCurve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
; but they are effectively treated as exact when comparing (to several decimal places) results from explicit formulae (such as those found elsewhere in this article) to the friction factor computed via Colebrook's implicit equation.
Equations similar to the additional forms above (with the constants rounded to fewer decimal places—or perhaps shifted slightly to minimize overall rounding errors) may be found in various references. It may be helpful to note that they are essentially the same equation.
Free surface flow
Another form of the Colebrook-White equation exists for free surfaces. Such a condition may exist in a pipe that is flowing partially full of fluid. For free surface flow:

Haaland equation
The Haaland equation is used to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation, but the discrepancy from experimental data is well within the accuracy of the data. It was developed by S. E. Haaland in 1983.
The Haaland equation is defined as:
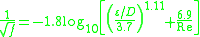
where:-
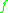 is the Darcy friction factor
is the Darcy friction factor -
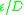 is the relative roughness
is the relative roughness -
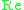 is the Reynolds number.
is the Reynolds number.
Swamee–Jain equation
The Swamee–Jain equation is used to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation.
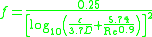
where f is a function of:- Roughness height, ε (m, ft)
- Pipe diameter, D (m, ft)
- Reynolds number, Re (unitless).
Serghides's solution
Serghides's solution is used to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation. It was derived using Steffensen's method.
The solution involves calculating three intermediate values and then substituting those values into a final equation.
where f is a function of:- Roughness height, ε (m, ft)
- Pipe diameter, D (m, ft)
- Reynolds number, Re (unitless).
The equation was found to match the Colebrook–White equation within 0.0023% for a test set with a 70-point matrix consisting of ten relative roughness values (in the range 0.00004 to 0.05) by seven Reynolds numbers (2500 to 108).
Goudar–Sonnad equation
Goudar equation is the most accurate approximation to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation. Equation has the following form
where f is a function of:- Roughness height, ε (m, ft)
- Pipe diameter, D (m, ft)
- Reynolds number, Re (unitless).
Brkić solution
Brkić shows one approximation of the Colebrook equation based on the Lambert W-function

where Darcy friction factor f is a function of:- Roughness height, ε (m, ft)
- Pipe diameter, D (m, ft)
- Reynolds number, Re (unitless).
The equation was found to match the Colebrook–White equation within 3.15%.
Blasius correlations
Early approximations by Blasius are given in terms of the Fanning friction factor in the Paul Richard Heinrich BlasiusPaul Richard Heinrich BlasiusPaul Richard Heinrich Blasius was a German fluid dynamics engineer.He was one of the first students of Prandtl who provided a mathematical basis for boundary-layer drag but also showed as early as 1911 that the resistance to flow through smooth pipes could be expressed in terms of the Reynolds...
article.
Further reading
For the section which includes the free-surface form of the equation — , p. 16. — Serghides' solution is also mentioned here.
External links
-