Cyclohedron
Encyclopedia
In geometry
, the cyclohedron or Bott–Taubes polytope is a certain (n − 1)-dimensional polytope
that is useful in studying knot invariant
s.
The configuration space
of n distinct points on the circle S1 is an n-dimensional manifold
, which can be compactified into a manifold with corners by allowing the points to approach each other. This compactification can be factored as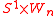
, where Wn is the cyclohedron.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the cyclohedron or Bott–Taubes polytope is a certain (n − 1)-dimensional polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
that is useful in studying knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
s.
The configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of n distinct points on the circle S1 is an n-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, which can be compactified into a manifold with corners by allowing the points to approach each other. This compactification can be factored as
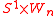, where Wn is the cyclohedron.