
Cut-elimination theorem
Encyclopedia
The cut-elimination theorem (or Gentzen's Hauptsatz) is the central result establishing the significance of the sequent calculus
. It was originally proved by Gerhard Gentzen
1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic
and classical logic
respectively. The cut-elimination theorem states that any judgement that possesses a proof in the sequent calculus that makes use of the cut rule also possesses a cut-free proof, that is, a proof that does not make use of the cut rule.
A sequent
is a logical expression relating multiple sentences, in the form " ", which is to be read as "A, B, C,
", which is to be read as "A, B, C,  proves N, O, P", and (as glossed by Gentzen) should be understood as equivalent to the truth-function "If (A and B and C
proves N, O, P", and (as glossed by Gentzen) should be understood as equivalent to the truth-function "If (A and B and C  ) then (N or O or P)." Note that the left-hand side (LHS) is a conjunction (and) and the RHS is a disjunction (or). The LHS may have arbitrarily many or few formulae; when the LHS is empty, the RHS is a tautology
) then (N or O or P)." Note that the left-hand side (LHS) is a conjunction (and) and the RHS is a disjunction (or). The LHS may have arbitrarily many or few formulae; when the LHS is empty, the RHS is a tautology
. In LK, the RHS may also have any number of formulae—if it has none, the LHS is a contradiction
, whereas in LJ the RHS may have only none or one formula: here we see that allowing more than one formula in the RHS is equivalent, in the presence of the right contraction rule, to the admissibility of the law of the excluded middle. However, the sequent calculus is a fairly expressive framework, and there have been sequent calculi for intuitionistic logic proposed that allow many formulae in the RHS. From Jean-Yves Girard
's logic LC it is easy to obtain a rather natural formalisation of classical logic where the RHS contains at most one formula; it is the interplay of the logical and structural rules that is the key here.
"Cut" is a rule in the normal statement of the sequent calculus
, and equivalent to a variety of rules in other proof theories
, which, given
and
allows one to infer
That is, it "cuts" the occurrences of the formula "C" out of the inferential relation.
The cut-elimination theorem states that (for a given system) any sequent provable using the rule Cut can be proved without use of this rule. If we think of as a theorem, then cut-elimination simply says that a lemma
as a theorem, then cut-elimination simply says that a lemma  used to prove this theorem can be inlined. Whenever the theorem's proof mentions lemma
used to prove this theorem can be inlined. Whenever the theorem's proof mentions lemma
 , we can substitute the occurrences for the proof of
, we can substitute the occurrences for the proof of  . Consequently, the cut rule is admissible
. Consequently, the cut rule is admissible
.
For systems formulated in the sequent calculus, analytic proof
s are those proofs that do not use Cut. Typically such a proof will be longer, of course, and not necessarily trivially so. In his essay "Don't Eliminate Cut!" George Boolos
demonstrated that there was a derivation that could be completed in a page using cut, but whose analytic proof could not be completed in the lifespan of the universe.
The theorem has many, rich consequences:
Cut elimination is one of the most powerful tools for proving interpolation theorem
s. The possibility of carrying out proof search based on resolution, the essential insight leading to the Prolog
programming language, depends upon the admissibility of Cut in the appropriate system.
For proof systems based on higher-order typed lambda calculus through a Curry–Howard isomorphism, cut elimination algorithms correspond to the strong normalization property (every proof term reduces in a finite number of step into a normal form
).
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
. It was originally proved by Gerhard Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
and classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
respectively. The cut-elimination theorem states that any judgement that possesses a proof in the sequent calculus that makes use of the cut rule also possesses a cut-free proof, that is, a proof that does not make use of the cut rule.
A sequent
Sequent
In proof theory, a sequent is a formalized statement of provability that is frequently used when specifying calculi for deduction. In the sequent calculus, the name sequent is used for the construct which can be regarded as a specific kind of judgment, characteristic to this deduction system.-...
is a logical expression relating multiple sentences, in the form "
 ", which is to be read as "A, B, C,
", which is to be read as "A, B, C,  proves N, O, P", and (as glossed by Gentzen) should be understood as equivalent to the truth-function "If (A and B and C
proves N, O, P", and (as glossed by Gentzen) should be understood as equivalent to the truth-function "If (A and B and C  ) then (N or O or P)." Note that the left-hand side (LHS) is a conjunction (and) and the RHS is a disjunction (or). The LHS may have arbitrarily many or few formulae; when the LHS is empty, the RHS is a tautology
) then (N or O or P)." Note that the left-hand side (LHS) is a conjunction (and) and the RHS is a disjunction (or). The LHS may have arbitrarily many or few formulae; when the LHS is empty, the RHS is a tautologyTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
. In LK, the RHS may also have any number of formulae—if it has none, the LHS is a contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
, whereas in LJ the RHS may have only none or one formula: here we see that allowing more than one formula in the RHS is equivalent, in the presence of the right contraction rule, to the admissibility of the law of the excluded middle. However, the sequent calculus is a fairly expressive framework, and there have been sequent calculi for intuitionistic logic proposed that allow many formulae in the RHS. From Jean-Yves Girard
Jean-Yves Girard
Jean-Yves Girard is a French logician working in proof theory. His contributions include a proof of strong normalization in a system of second-order logic called system F; the invention of linear logic; the geometry of interaction; and ludics...
's logic LC it is easy to obtain a rather natural formalisation of classical logic where the RHS contains at most one formula; it is the interplay of the logical and structural rules that is the key here.
"Cut" is a rule in the normal statement of the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, and equivalent to a variety of rules in other proof theories
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, which, given
- (1)

and
- (2)
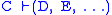
allows one to infer
- (3)
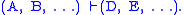
That is, it "cuts" the occurrences of the formula "C" out of the inferential relation.
The cut-elimination theorem states that (for a given system) any sequent provable using the rule Cut can be proved without use of this rule. If we think of
 as a theorem, then cut-elimination simply says that a lemma
as a theorem, then cut-elimination simply says that a lemma  used to prove this theorem can be inlined. Whenever the theorem's proof mentions lemma
used to prove this theorem can be inlined. Whenever the theorem's proof mentions lemmaLemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
 , we can substitute the occurrences for the proof of
, we can substitute the occurrences for the proof of  . Consequently, the cut rule is admissible
. Consequently, the cut rule is admissibleAdmissible rule
In logic, a rule of inference is admissible in a formal system if the set of theorems of the system does not change when that rule is added to the existing rules of the system. In other words, every formula that can be derived using that rule is already derivable without that rule, so, in a sense,...
.
For systems formulated in the sequent calculus, analytic proof
Analytic proof
In mathematical analysis, an analytical proof is a proof of a theorem in analysis that only makes use of methods from analysis, and which does not make use of results from geometry...
s are those proofs that do not use Cut. Typically such a proof will be longer, of course, and not necessarily trivially so. In his essay "Don't Eliminate Cut!" George Boolos
George Boolos
George Stephen Boolos was a philosopher and a mathematical logician who taught at the Massachusetts Institute of Technology.- Life :...
demonstrated that there was a derivation that could be completed in a page using cut, but whose analytic proof could not be completed in the lifespan of the universe.
The theorem has many, rich consequences:
- A system is inconsistentConsistency proofIn logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
if it admits a proof of the absurd. If the system has a cut elimination theorem, then if it has a proof of the absurd, or of the empty sequent, it should also have a proof of the absurd (or the empty sequent), without cuts. It is typically very easy to check that there are no such proofs. Thus, once a system is shown to have a cut elimination theorem, it is normally immediate that the system is consistent. - Normally also the system has, at least in first order logic, the subformula property, an important property in several approaches to proof-theoretic semanticsProof-theoretic semanticsProof-theoretic semantics is an approach to the semantics of logic that attempts to locate the meaning of propositions and logical connectives not in terms of interpretations, as in Tarskian approaches to semantics, but in the role that the proposition or logical connective plays within the system...
.
Cut elimination is one of the most powerful tools for proving interpolation theorem
Craig interpolation
In mathematical logic, Craig's interpolation theorem is a result about the relationship between different logical theories. Roughly stated, the theorem says that if a formula φ implies a formula ψ then there is a third formula ρ, called an interpolant, such that every nonlogical symbol...
s. The possibility of carrying out proof search based on resolution, the essential insight leading to the Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
programming language, depends upon the admissibility of Cut in the appropriate system.
For proof systems based on higher-order typed lambda calculus through a Curry–Howard isomorphism, cut elimination algorithms correspond to the strong normalization property (every proof term reduces in a finite number of step into a normal form
Normal form (term rewriting)
In abstract rewriting, a normal form is an element of the system which cannot be rewritten any further. Stated formally, for some reduction relation ⋅ → ⋅ over X a term t in X is a normal form if there does not exist a term t′ in X such that t → t′.Consider...
).

