
Consistency proof
Encyclopedia
In logic
, a consistent theory
is one that does not contain a contradiction
. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if
it has a model, i.e. there exists an interpretation
under which all formulas
in the theory are true. This is the sense used in traditional Aristotelian logic
, although in contemporary mathematical logic the term satisfiable is used instead. The syntactic definition states that a theory is consistent if and only if there is no formula P such that both P and its negation are provable from the axioms of the theory under its associated deductive system.
If these semantic and syntactic definitions are equivalent for a particular logic, the logic is complete. The completeness of sentential calculus was proved by Paul Bernays
in 1918 and Emil Post in 1921, while the completeness of predicate calculus was proved by Kurt Gödel
in 1930, and consistency proofs for arithmetics restricted with respect to the induction axiom schema
were proved by Ackermann (1924), von Neumann (1927) and Herbrand (1931). Stronger logics, such as second-order logic
, are not complete.
A consistency proof is a mathematical proof
that a particular theory is consistent. The early development of mathematical proof theory
was driven by the desire to provide finitary consistency proofs for all of mathematics as part of Hilbert's program
. Hilbert's program was strongly impacted by incompleteness theorems
, which showed that sufficiently strong proof theories cannot prove their own consistency (provided that they are in fact consistent).
Although consistency can be proved by means of model theory, it is often done in a purely syntactical way, without any need to reference some model of the logic. The cut-elimination (or equivalently the normalization of the underlying calculus if there is one) implies the consistency of the calculus: since there is obviously no cut-free proof of falsity, there is no contradiction in general.
. A theory is complete if, for every formula φ in its language, at least one of φ or ¬ φ is a logical consequence of the theory.
Presburger arithmetic
is an axiom system for the natural numbers under addition. It is both consistent and complete.
Gödel's incompleteness theorems
show that any sufficiently strong effective theory of arithmetic cannot be both complete and consistent. Gödel's theorem applies to the theories of Peano arithmetic (PA) and Primitive recursive arithmetic
(PRA), but not to Presburger arithmetic
.
Moreover, Gödel's second incompleteness theorem shows that the consistency of sufficiently strong effective theories of arithmetic can be tested in a particular way. Such a theory is consistent if and only if it does not prove a particular sentence, called the Gödel sentence of the theory, which is a formalized statement of the claim that the theory is indeed consistent. Thus the consistency of a sufficiently strong, effective, consistent theory of arithmetic can never be proven in that system itself. The same result is true for effective theories that can describe a strong enough fragment of arithmetic – including set theories such as Zermelo–Fraenkel set theory
. These set theories cannot prove their own Gödel sentences – provided that they are consistent, which is generally believed.
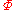 in first-order logic is consistent (written Con
in first-order logic is consistent (written Con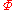 ) if and only if
) if and only if
there is no formula such that
such that  and
and  . Otherwise
. Otherwise 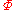 is inconsistent and is written Inc
is inconsistent and is written Inc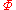 .
.
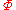 is said to be simply consistent if and only if
is said to be simply consistent if and only if
for no formula of
of 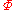 , both
, both  and the negation
and the negation
of are theorems of
are theorems of 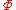 .
.
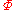 is said to be absolutely consistent or Post consistent if and only if at least one formula of
is said to be absolutely consistent or Post consistent if and only if at least one formula of 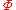 is not a theorem of
is not a theorem of 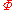 .
.
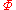 is said to be maximally consistent if and only if for every formula
is said to be maximally consistent if and only if for every formula  , if Con (
, if Con (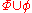 ) then
) then 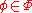 .
.
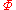 is said to contain witnesses if and only if for every formula of the form
is said to contain witnesses if and only if for every formula of the form  there exists a term
there exists a term  such that
such that 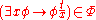 . See First-order logic
. See First-order logic
.
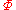 be a maximally consistent set of
be a maximally consistent set of 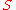 -formulas containing witnesses.
-formulas containing witnesses.
Define a binary relation on the set of
on the set of  -terms such that
-terms such that 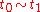 if and only if
if and only if 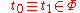 ; and let
; and let  denote the equivalence class of terms containing
denote the equivalence class of terms containing  ; and let
; and let  where
where 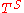 is the set of terms based on the symbol set
is the set of terms based on the symbol set 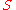 .
.
Define the -structure
-structure  over
over  the term-structure corresponding to
the term-structure corresponding to 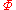 by:
by:
Let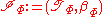 be the term interpretation associated with
be the term interpretation associated with 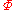 , where
, where  .
.
For all ,
,  if and only if
if and only if 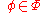 .
.
 is an equivalence relation
is an equivalence relation
. Then, it needs to be verified that (1), (2), and (3) are well defined. This falls out of the fact that is an equivalence relation and also requires a proof that (1) and (2) are independent of the choice of
is an equivalence relation and also requires a proof that (1) and (2) are independent of the choice of  class representatives. Finally,
class representatives. Finally,  can be verified by induction on formulas.
can be verified by induction on formulas.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, a consistent theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
is one that does not contain a contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it has a model, i.e. there exists an interpretation
Interpretation (model theory)
In model theory, interpretation of a structure M in another structure N is a technical notion that approximates the idea of representing M inside N. For example every reduct or definitional expansion of a structure N has an interpretation in N.Many model-theoretic properties are preserved under...
under which all formulas
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
in the theory are true. This is the sense used in traditional Aristotelian logic
Term logic
In philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
, although in contemporary mathematical logic the term satisfiable is used instead. The syntactic definition states that a theory is consistent if and only if there is no formula P such that both P and its negation are provable from the axioms of the theory under its associated deductive system.
If these semantic and syntactic definitions are equivalent for a particular logic, the logic is complete. The completeness of sentential calculus was proved by Paul Bernays
Paul Bernays
Paul Isaac Bernays was a Swiss mathematician, who made significant contributions to mathematical logic, axiomatic set theory, and the philosophy of mathematics. He was an assistant to, and close collaborator of, David Hilbert.-Biography:Bernays spent his childhood in Berlin. Bernays attended the...
in 1918 and Emil Post in 1921, while the completeness of predicate calculus was proved by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in 1930, and consistency proofs for arithmetics restricted with respect to the induction axiom schema
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
were proved by Ackermann (1924), von Neumann (1927) and Herbrand (1931). Stronger logics, such as second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
, are not complete.
A consistency proof is a mathematical proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that a particular theory is consistent. The early development of mathematical proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
was driven by the desire to provide finitary consistency proofs for all of mathematics as part of Hilbert's program
Hilbert's program
In mathematics, Hilbert's program, formulated by German mathematician David Hilbert, was a proposed solution to the foundational crisis of mathematics, when early attempts to clarify the foundations of mathematics were found to suffer from paradoxes and inconsistencies...
. Hilbert's program was strongly impacted by incompleteness theorems
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
, which showed that sufficiently strong proof theories cannot prove their own consistency (provided that they are in fact consistent).
Although consistency can be proved by means of model theory, it is often done in a purely syntactical way, without any need to reference some model of the logic. The cut-elimination (or equivalently the normalization of the underlying calculus if there is one) implies the consistency of the calculus: since there is obviously no cut-free proof of falsity, there is no contradiction in general.
Consistency and completeness in arithmetic
In theories of arithmetic, such as Peano arithmetic, there is an intricate relationship between the consistency of the theory and its completenessCompleteness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
. A theory is complete if, for every formula φ in its language, at least one of φ or ¬ φ is a logical consequence of the theory.
Presburger arithmetic
Presburger arithmetic
Presburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
is an axiom system for the natural numbers under addition. It is both consistent and complete.
Gödel's incompleteness theorems
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
show that any sufficiently strong effective theory of arithmetic cannot be both complete and consistent. Gödel's theorem applies to the theories of Peano arithmetic (PA) and Primitive recursive arithmetic
Primitive recursive arithmetic
Primitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
(PRA), but not to Presburger arithmetic
Presburger arithmetic
Presburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
.
Moreover, Gödel's second incompleteness theorem shows that the consistency of sufficiently strong effective theories of arithmetic can be tested in a particular way. Such a theory is consistent if and only if it does not prove a particular sentence, called the Gödel sentence of the theory, which is a formalized statement of the claim that the theory is indeed consistent. Thus the consistency of a sufficiently strong, effective, consistent theory of arithmetic can never be proven in that system itself. The same result is true for effective theories that can describe a strong enough fragment of arithmetic – including set theories such as Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
. These set theories cannot prove their own Gödel sentences – provided that they are consistent, which is generally believed.
Formulas
A set of formulas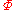 in first-order logic is consistent (written Con
in first-order logic is consistent (written Con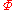 ) if and only if
) if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is no formula
 such that
such that  and
and  . Otherwise
. Otherwise 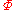 is inconsistent and is written Inc
is inconsistent and is written Inc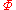 .
.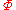 is said to be simply consistent if and only if
is said to be simply consistent if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for no formula
 of
of 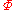 , both
, both  and the negation
and the negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
of
 are theorems of
are theorems of 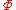 .
.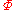 is said to be absolutely consistent or Post consistent if and only if at least one formula of
is said to be absolutely consistent or Post consistent if and only if at least one formula of 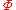 is not a theorem of
is not a theorem of 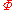 .
.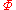 is said to be maximally consistent if and only if for every formula
is said to be maximally consistent if and only if for every formula  , if Con (
, if Con (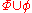 ) then
) then 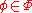 .
.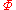 is said to contain witnesses if and only if for every formula of the form
is said to contain witnesses if and only if for every formula of the form  there exists a term
there exists a term  such that
such that 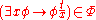 . See First-order logic
. See First-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.
Basic results
- The following are equivalent:
- Inc
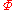
- For all

- Inc
- Every satisfiable set of formulas is consistent, where a set of formulas
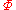 is satisfiable if and only if there exists a model
is satisfiable if and only if there exists a model  such that
such that  .
. - For all
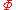 and
and  :
:
- if not
 , then Con
, then Con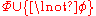 ;
; - if Con
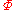 and
and  , then Con
, then Con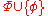 ;
; - if Con
 , then Con
, then Con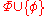 or Con
or Con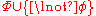 .
.
- if not
- Let
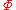 be a maximally consistent set of formulas and contain witnesses. For all
be a maximally consistent set of formulas and contain witnesses. For all  and
and 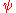 :
:
- if
 , then
, then 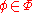 ,
, - either
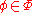 or
or  ,
, -
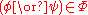 if and only if
if and only if 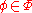 or
or 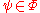 ,
, - if
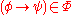 and
and 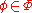 , then
, then 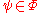 ,
, -
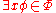 if and only if there is a term
if and only if there is a term  such that
such that 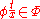 .
.
- if
Henkin's theorem
Let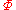 be a maximally consistent set of
be a maximally consistent set of 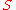 -formulas containing witnesses.
-formulas containing witnesses.Define a binary relation
 on the set of
on the set of  -terms such that
-terms such that 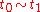 if and only if
if and only if 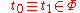 ; and let
; and let  denote the equivalence class of terms containing
denote the equivalence class of terms containing  ; and let
; and let  where
where 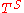 is the set of terms based on the symbol set
is the set of terms based on the symbol set 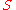 .
.Define the
 -structure
-structure  over
over  the term-structure corresponding to
the term-structure corresponding to 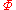 by:
by:- for
 -ary
-ary 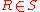 ,
,  if and only if
if and only if 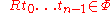 ;
; - for
 -ary
-ary 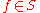 ,
,  ;
; - for
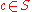 ,
,  .
.
Let
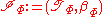 be the term interpretation associated with
be the term interpretation associated with 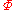 , where
, where  .
.For all
 ,
,  if and only if
if and only if 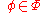 .
.Sketch of proof
There are several things to verify. First, that is an equivalence relation
is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. Then, it needs to be verified that (1), (2), and (3) are well defined. This falls out of the fact that
 is an equivalence relation and also requires a proof that (1) and (2) are independent of the choice of
is an equivalence relation and also requires a proof that (1) and (2) are independent of the choice of  class representatives. Finally,
class representatives. Finally,  can be verified by induction on formulas.
can be verified by induction on formulas.See also
- EquiconsistencyEquiconsistencyIn mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
- Hilbert's problemsHilbert's problemsHilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
- Hilbert's second problemHilbert's second problemIn mathematics, Hilbert's second problem was posed by David Hilbert in 1900 as one of his 23 problems. It asks for a proof that arithmetic is consistent – free of any internal contradictions....
- Jan Łukasiewicz
- Matiyasevich's theorem
- ω-consistency

