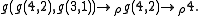Normal form (term rewriting)
Encyclopedia
In abstract rewriting, a normal form is an element of the system which cannot be rewritten any further. Stated formally, for some reduction relation ⋅ → ⋅ over X a term t in X is a normal form if there does not exist a term t′ in X such that t → t′.
Consider the basic term rewriting system with reduction rule ρ : g(x, y) → x. The term g(g(4, 2), g(3, 1)) has the following reduction sequence, according to the usual outermost strategy, that is, if the reduction rule is applied to each outermost occurrence of g:
There is no rule that permits us to rewrite 4, so 4 is a normal form for this term rewriting system.
Related concepts refer to the possibility of rewriting an element into normal form. Weak normalization means that some element can be rewritten into a normal form. Strong normalization means that any reduction sequence starting from some element terminates. We say that the system is weakly normalizing (or strongly normalizing) if all elements are weakly normalizing (resp. strongly normalizing).
Newman's lemma
states that if an abstract reduction system A is strongly normalizing and is weakly confluent
, then A is in fact confluent. The result enables us to further generalize the critical pair lemma.
Consider the basic term rewriting system with reduction rule ρ : g(x, y) → x. The term g(g(4, 2), g(3, 1)) has the following reduction sequence, according to the usual outermost strategy, that is, if the reduction rule is applied to each outermost occurrence of g:
There is no rule that permits us to rewrite 4, so 4 is a normal form for this term rewriting system.
Related concepts refer to the possibility of rewriting an element into normal form. Weak normalization means that some element can be rewritten into a normal form. Strong normalization means that any reduction sequence starting from some element terminates. We say that the system is weakly normalizing (or strongly normalizing) if all elements are weakly normalizing (resp. strongly normalizing).
Newman's lemma
Newman's lemma
In the theory of rewriting systems, Newman's lemma states that a terminating abstract rewriting system , that is, one in which there are no infinite reduction sequences, is confluent if it is locally confluent...
states that if an abstract reduction system A is strongly normalizing and is weakly confluent
Confluence (term rewriting)
In computer science, confluence is a property of rewriting systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.- Motivating example :Consider...
, then A is in fact confluent. The result enables us to further generalize the critical pair lemma.