Császár polyhedron
Type	Toroidal polyhedron Toroidal polyhedron In geometry, a toroidal polyhedron is a polyhedron with a genus of 1 or greater, representing topological torus surfaces.Non-self-intersecting toroidal polyhedra are embedded tori, while self-intersecting toroidal polyhedra are toroidal as abstract polyhedra, which can be verified by their Euler...
Faces	14 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s
Edges	21
Vertices	7
Euler characteristic Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...	0
Genus Genus (mathematics) In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...	1
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...	3.3.3.3.3.3
Symmetry group	C2
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	Szilassi polyhedron Szilassi polyhedron The Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem...
Properties	Nonconvex

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the Császár polyhedron (ˈtʃaːsaːr) is a nonconvex polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

, topologically a toroid

Toroid

Toroid may refer to*Toroid , a doughnut-like solid whose surface is a torus.*Toroidal inductors and transformers which have wire windings on circular ring shaped magnetic cores.*Vortex ring, a toroidal flow in fluid mechanics....

, with 14 triangular faces

Face (geometry)

In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

.

This polyhedron has no diagonal

Diagonal

A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...

s; every pair of vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

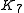  onto a topological torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

. Of the 35 possible triangles from vertices of the polyhedron, only 14 are faces. If the seven vertices are numbered 1 through 7, the torus can be cut open to form a sheet topologically equivalent to this:

    5———4———7———2

   / \ / \ / \ / \

  6———1———3———5———4

 / \ / \ / \ /

4———7———2———6

         \ /

          4

This pattern can be used to tile the plane. In the animated figure above right, the faces are the following (vertex 1 being at the top):

• Light blue:

(1, 2, 3)
(1, 3, 4)
(1, 4, 5)
(1, 5, 6)
(1, 6, 7)
(1, 7, 2)
(2, 3, 6)
(6, 3, 5)

• Yellow

(3, 5, 7)
(7, 5, 2)

• Green

(6, 2, 4)
(4, 2, 5)

• Dark blue

(4, 6, 7)
(4, 7, 3)

In this numbering, the layout of the vertices at the end of the video clip, going clockwise from vertex 1, is 1, 2, 5, 4, 3, 7, 6, 5, 2, 7, 3, 4, 5, 6, 7.

There is some freedom in the positioning of the vertices, but some arrangements will lead to faces intersecting one another and no hole being formed.

All vertices are topologically equivalent, as can be seen from the tesselation of the plane that uses the above diagram.

The tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 and the Császár polyhedron are the only two known polyhedra (having a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 boundary) without any diagonals, although there are other known polyhedra such as the Schönhardt polyhedron

Schönhardt polyhedron

In geometry, the Schönhardt polyhedron is the simplest non-convex polyhedron that cannot be triangulated into tetrahedra without adding new vertices...

 for which there are no interior diagonals (that is, all diagonals are outside the polyhedron) as well as non-manifold surfaces with no diagonals . If a polyhedron with v vertices is embedded onto a surface with h holes, in such a way that every pair of vertices is connected by an edge, it follows by some manipulation of the Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

 that
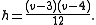
This equation is satisfied for the tetrahedron with h = 0 and v = 4, and for the Császár polyhedron with h = 1 and v = 7. The next possible solution, h = 6 and v = 12, would correspond to a polyhedron with 44 faces and 66 edges, but it is not realizable as a polyhedron; it is not known whether such a polyhedron exists with a higher genus . More generally, this equation can be satisfied only when v is congruent to 0, 3, 4, or 7 modulo

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

 12 .

The Császár polyhedron is named after Hungarian topologist Ákos Császár

Ákos Császár

Ákos Császár is a Hungarian mathematician, specializing in general topology and real analysis. He discovered the Császár polyhedron, a nonconvex polyhedron without diagonals...

, who discovered it in 1949. The dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

 to the Császár polyhedron, the Szilassi polyhedron

Szilassi polyhedron

The Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem...

, was discovered later, in 1977, by Lajos Szilassi; it has 14 vertices, 21 edges, and seven hexagonal faces, each sharing an edge with every other face. Like the Császár polyhedron, the Szilassi polyhedron has the topology of a torus.