
Cramér's theorem
Encyclopedia
In mathematical statistics
, Cramér's theorem (or Cramér’s decomposition theorem) is one of several theorems of Harald Cramér
, a Swedish
statistician
and probabilist
.
random variable
s whose sum X + Y is a normal random variable, then both X and Y must be normal as well. By induction
, if any finite sum of independent real-valued random variables is normal, then the summands must all be normal.
Thus, while the normal distribution is infinitely divisible
, it can only be decomposed into normal distributions (if the summands are independent).
Contrast with the central limit theorem
, which states that the average of independent identically distributed random variables with finite mean and variance is asymptotically normal. Cramér's theorem shows that a finite average is not normal, unless the original variables were normal.
, that in this case the sequence
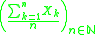
converges in probability to the mean
of the probability distribution of Xk. Cramér's theorem in this sense states that the probabilities of "large deviations
" away from the mean in this sequence decay exponentially with the rate
given by the Cramér function, which is the Legendre transform
of the cumulant
-generating function of Xk.
. This theorem extends some properties of algebraic operations on convergent sequences
of real number
s to sequences of random variable
s.
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
, Cramér's theorem (or Cramér’s decomposition theorem) is one of several theorems of Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
, a Swedish
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
statistician
Statistician
A statistician is someone who works with theoretical or applied statistics. The profession exists in both the private and public sectors. The core of that work is to measure, interpret, and describe the world and human activity patterns within it...
and probabilist
Probabilist
A probabilist is either:* A follower of probabilism * A mathematician who practices probability theory; see List of mathematical probabilists...
.
Normal random variables
Cramér's theorem is the result that if X and Y are independent real-valuedReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s whose sum X + Y is a normal random variable, then both X and Y must be normal as well. By induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, if any finite sum of independent real-valued random variables is normal, then the summands must all be normal.
Thus, while the normal distribution is infinitely divisible
Infinite divisibility (probability)
The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
, it can only be decomposed into normal distributions (if the summands are independent).
Contrast with the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, which states that the average of independent identically distributed random variables with finite mean and variance is asymptotically normal. Cramér's theorem shows that a finite average is not normal, unless the original variables were normal.
Large deviations
Cramér's theorem may also refer to another result of the same mathematician concerning the partial sums of a sequence of independent, identically distributed random variables, say X1, X2, X3, …. It is well known, by the law of large numbersLaw of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, that in this case the sequence
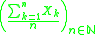
converges in probability to the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the probability distribution of Xk. Cramér's theorem in this sense states that the probabilities of "large deviations
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
" away from the mean in this sequence decay exponentially with the rate
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
given by the Cramér function, which is the Legendre transform
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
-generating function of Xk.
Slutsky's theorem
Slutsky’s theorem is also attributed to Harald CramérHarald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
. This theorem extends some properties of algebraic operations on convergent sequences
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s to sequences of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s.
See also
- Cochran's theoremCochran's theoremIn statistics, Cochran's theorem, devised by William G. Cochran, is a theorem used in to justify results relating to the probability distributions of statistics that are used in the analysis of variance.- Statement :...
, on decomposing sum of squares of normal distributions - Indecomposable distributionIndecomposable distributionIn probability theory, an indecomposable distribution is a probability distribution that cannot be represented as the distribution of the sum of two or more non-constant independent random variables: Z ≠ X + Y. If it can be so expressed, it is decomposable:...
, on decomposability - Raikov's theoremRaikov's theoremIn probability theory, Raikov’s theorem, named after Dmitry Raikov, states that if the sum of two independent random variables X and Y has a Poisson distribution, then both X and Y themselves must have the Poisson distribution. It says the same thing about the Poisson distribution that Cramér's...
, on the decomposition of Poisson distributions - Infinite divisibility (probability)Infinite divisibility (probability)The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...

