Bipartite dimension
Encyclopedia
In the mathematical field of graph theory
, the bipartite dimension of a graph
G = (V, E) is the minimum number of bicliques, that is, complete bipartite subgraphs, needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes biclique cover. The bipartite dimension of G is often denoted by the symbol d(G).
crown graph
equals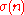
, where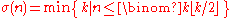
is the inverse function of the central binomial coefficient
.
determine the bipartite dimension for some special graphs. For example, the path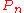
has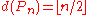
, the cycle 
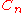has 
,
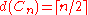and the complete graph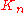
has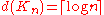 
.
. The decision problem
for bipartite dimension can be phrased as:
This problem appears as problem GT18 in Garey and Johnson's classical book on NP-completeness, and is a rather straightforward reformulation of
another decision problem on families of finite sets.
The set basis problem appears as problem SP7 in Garey and Johnson's book.
Here, for a family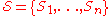
of subsets of a finite set 
,
a set basis for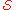
is another family of subsets 
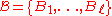of 
, such that every set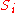 
can be described as the union of some basis elements from 
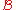. The set basis problem is now given as follows:
In its former formulation, the problem was proved to be NP-complete
by , even for bipartite graph
s. The formulation as a set basis problem was proved to be NP-complete earlier by . The problem remains NP-hard even if we restrict our attention to bipartite graphs whose bipartite dimension is guaranteed to be at most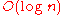
, with n denoting the size of the given problem instance . On the positive side, the problem is solvable in polynomial time on bipartite domino-free graphs .
Regarding the existence of approximation algorithm
s, proved that the problem cannot be approximated well (assuming P ≠ NP). Indeed, the bipartite dimension is NP-hard to approximate
within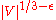
for every fixed 
, already for bipartite graphs .
In contrast, proving that the problem is fixed-parameter tractable is an exercise in designing kernelization algorithms
, which appears as such in the textbook by . also provide a concrete bound on the size of the resulting kernel, which has meanwhile been improved by .
In fact, for a given bipartite graph on n vertices, it can be decided in time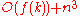
with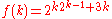 
whether its bipartite dimension is at most k
established a relation between the size of a maximum matching and the bipartite dimension. More precisely, they showed that for a graph G with m edges that admits a matching of size
the following holds: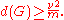
system, a role provides access rights to a set of resources. A user can own multiple roles, and he has permission to access all resources granted by some of his roles. Also, a role can be owned by multiple users. The role mining problem is to find a minimum set of roles, such that for each user, his roles taken together grant access to all specified resources. The set of users together with the set of resources in the system naturally induces a bipartite graph, whose edges are permissions. Each biclique in this graph is a potential role, and the optimum solutions to the role mining problem are precisely the minimum biclique edge covers .
A similar scenario is known in computer security
, more specifically in secure broadcast
ing. In that setup, several messages need to be sent each to a set of receivers, over an insecure channel. Each message has to be encrypted using some cryptographic key that is known only to the intended receivers. Each receiver may possess multiple encryption keys, and each key will be distributed to multiple receivers. The optimum key generation problem is to find a minimum set of encryption keys for ensuring secure transmission. As above, the problem can be modeled using a bipartite graph whose minimum biclique edge covers coincide with the solutions to the optimum key generation problem .
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the bipartite dimension of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G = (V, E) is the minimum number of bicliques, that is, complete bipartite subgraphs, needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes biclique cover. The bipartite dimension of G is often denoted by the symbol d(G).
Bipartite dimension formulas for some graphs
The bipartite dimension of a 2n-vertexcrown graph
Crown graph
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j...
equals
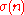, where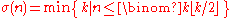is the inverse function of the central binomial coefficient
Central binomial coefficient
In mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient byThey are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle...
.
determine the bipartite dimension for some special graphs. For example, the path
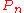
has
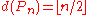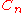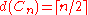, the cycle has ,and the complete graph
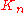has 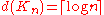.Computing the bipartite dimension
The computational task of determining the bipartite dimension for a given graph G is an optimization problemOptimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
. The decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
for bipartite dimension can be phrased as:
- INSTANCE: A graph
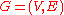and a positive integer 
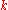. - QUESTION: Does G admit a biclique edge cover containing at most
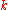bicliques?
This problem appears as problem GT18 in Garey and Johnson's classical book on NP-completeness, and is a rather straightforward reformulation of
another decision problem on families of finite sets.
The set basis problem appears as problem SP7 in Garey and Johnson's book.
Here, for a family
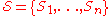of subsets of a finite set ,a set basis for
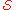is another family of subsets 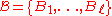of , such that every set 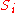can be described as the union of some basis elements from 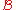. The set basis problem is now given as follows:- INSTANCE: A finite set
, a family 
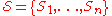of subsets of 
, and a positive integer k. - QUESTION: Does there exist a set basis of size at most
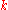for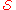 
?
In its former formulation, the problem was proved to be NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
by , even for bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s. The formulation as a set basis problem was proved to be NP-complete earlier by . The problem remains NP-hard even if we restrict our attention to bipartite graphs whose bipartite dimension is guaranteed to be at most
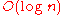, with n denoting the size of the given problem instance . On the positive side, the problem is solvable in polynomial time on bipartite domino-free graphs .Regarding the existence of approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s, proved that the problem cannot be approximated well (assuming P ≠ NP). Indeed, the bipartite dimension is NP-hard to approximate
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
within
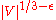for every fixed , already for bipartite graphs .In contrast, proving that the problem is fixed-parameter tractable is an exercise in designing kernelization algorithms
Kernelization
In computer science, a kernelization is an efficient algorithm that preprocesses instances of decision problems by mapping them to equivalent instances with a guaranteed upper bound on the size of the output, called the kernel of the instance. Kernelization is often achieved by applying a set of...
, which appears as such in the textbook by . also provide a concrete bound on the size of the resulting kernel, which has meanwhile been improved by .
In fact, for a given bipartite graph on n vertices, it can be decided in time
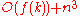with 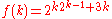whether its bipartite dimension is at most k Bounds
Although determining the bipartite dimension is computationally hard, quite a few estimates are available. For instance,established a relation between the size of a maximum matching and the bipartite dimension. More precisely, they showed that for a graph G with m edges that admits a matching of size
the following holds: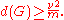Applications
The problem of determining the bipartite dimension of a graph appears in various contexts of computing. For instance, in computer systems, different users of a system can be allowed or disallowed accessing various resources. In a role-based access controlRole-Based Access Control
In computer systems security, role-based access control is an approach to restricting system access to authorized users. It is used by the majority of enterprises with more than 500 employees, and can be implemented via mandatory access control or discretionary access control...
system, a role provides access rights to a set of resources. A user can own multiple roles, and he has permission to access all resources granted by some of his roles. Also, a role can be owned by multiple users. The role mining problem is to find a minimum set of roles, such that for each user, his roles taken together grant access to all specified resources. The set of users together with the set of resources in the system naturally induces a bipartite graph, whose edges are permissions. Each biclique in this graph is a potential role, and the optimum solutions to the role mining problem are precisely the minimum biclique edge covers .
A similar scenario is known in computer security
Computer security
Computer security is a branch of computer technology known as information security as applied to computers and networks. The objective of computer security includes protection of information and property from theft, corruption, or natural disaster, while allowing the information and property to...
, more specifically in secure broadcast
Broadcast
Broadcast or Broadcasting may refer to:* Broadcasting, the transmission of audio and video signals* Broadcast, an individual television program or radio program* Broadcast , an English electronic music band...
ing. In that setup, several messages need to be sent each to a set of receivers, over an insecure channel. Each message has to be encrypted using some cryptographic key that is known only to the intended receivers. Each receiver may possess multiple encryption keys, and each key will be distributed to multiple receivers. The optimum key generation problem is to find a minimum set of encryption keys for ensuring secure transmission. As above, the problem can be modeled using a bipartite graph whose minimum biclique edge covers coincide with the solutions to the optimum key generation problem .
See also
- List of NP-complete problems
- Intersection number (graph theory)Intersection number (graph theory)In the mathematical field of graph theory, the intersection number of a graph is the smallest number of elements in a representation of as an intersection graph of finite sets...
, the minimum number of cliquesClique (graph theory)In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
needed to cover the edges of a graph
External links
- blog entry about bipartite dimension by David EppsteinDavid EppsteinDavid Arthur Eppstein is an American computer scientist and mathematician. He is professor of computer science at University of California, Irvine. He is known for his work in computational geometry, graph algorithms, and recreational mathematics.-Biography:Born in England of New Zealander...