
Covariance group
Encyclopedia
In physics
, covariance group is a group
of coordinate transformations between admissible frames of reference
(see for example). The frames are assumed to provide equivalent description of physical phenomena. The covariance principle suggests the equations, describing the laws of physics, should transform from one admitted frame to another covariantly, that is, according to a representation
of the covariance group.
In special relativity
only inertial frames
are admitted and the covariance group consists of rotations
, velocity boosts
, and the parity transformation
. It is denoted as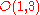
and is often referred to as Lorentz group
.
For example, the Maxwell equation with sources,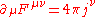 ,
,
transforms as a four-vector
, that is, under the (½,½) representation of the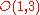 group.
group.
The Dirac equation,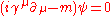 ,
,
transforms as a bispinor
, that is, under the (½,0)⊕(0,½) representation of the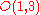 group.
group.
The covariance principle, unlike the relativity principle
, does not imply that the equations are invariant
under transformations from the covariance group. In practice the equations for electromagnetic and strong
interactions are invariant, while the weak interaction
is not invariant under the parity transformation. For example, the Maxwell equation is invariant, while the corresponding equation for the weak field explicitly contains left currents and thus is not invariant under the parity transformation.
In general relativity
the covariance group consists of all arbitrary (invertible and suitably differentiable) coordinate transformations.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, covariance group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of coordinate transformations between admissible frames of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
(see for example). The frames are assumed to provide equivalent description of physical phenomena. The covariance principle suggests the equations, describing the laws of physics, should transform from one admitted frame to another covariantly, that is, according to a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the covariance group.
In special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
only inertial frames
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
are admitted and the covariance group consists of rotations
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
, velocity boosts
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
, and the parity transformation
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
. It is denoted as
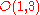
Generalized orthogonal group
In mathematics, the indefinite orthogonal group, O is the Lie group of all linear transformations of a n = p + q dimensional real vector space which leave invariant a nondegenerate, symmetric bilinear form of signature...
and is often referred to as Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
For example, the Maxwell equation with sources,
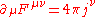 ,
,transforms as a four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
, that is, under the (½,½) representation of the
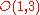 group.
group.The Dirac equation,
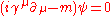 ,
,transforms as a bispinor
Bispinor
In physics, bispinor is a four-component object which transforms under the ⊕ representation of the covariance group of special relativity...
, that is, under the (½,0)⊕(0,½) representation of the
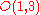 group.
group.The covariance principle, unlike the relativity principle
Principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
, does not imply that the equations are invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
under transformations from the covariance group. In practice the equations for electromagnetic and strong
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
interactions are invariant, while the weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
is not invariant under the parity transformation. For example, the Maxwell equation is invariant, while the corresponding equation for the weak field explicitly contains left currents and thus is not invariant under the parity transformation.
In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
the covariance group consists of all arbitrary (invertible and suitably differentiable) coordinate transformations.

