
Counting points on elliptic curves
Encyclopedia
An important aspect in the study of elliptic curves is devising effective ways of counting points on the curve. There have been several approaches to do so, and the algorithms devised have proved to be useful tools in the study of various fields such as number theory
, and more recently in cryptography
and Digital Signature Authentication (See elliptic curve cryptography
and elliptic curve DSA
). While in number theory they have important consequences in the solving of Diophantine equations, with respect to cryptography, they enable us to make effective use of the difficulty of the discrete logarithm problem (DLP) for the group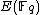 , of elliptic curves over a finite field
, of elliptic curves over a finite field
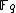 , where q = pk and p is a prime. The DLP, as it has come to be known, is a widely used approach to Public key cryptography, and the difficulty in solving this problem determines the level of security of the cryptosystem. This article covers algorithms to count points on elliptic curves over fields of large characteristic, in particular p > 3. For curves over fields of small characteristic more efficient algorithms based on p-adic methods exist.
, where q = pk and p is a prime. The DLP, as it has come to be known, is a widely used approach to Public key cryptography, and the difficulty in solving this problem determines the level of security of the cryptosystem. This article covers algorithms to count points on elliptic curves over fields of large characteristic, in particular p > 3. For curves over fields of small characteristic more efficient algorithms based on p-adic methods exist.
Several algorithms make use of the fact that groups of the form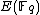 are subject to an important theorem due to Hasse, that bounds the number of points to be considered.
are subject to an important theorem due to Hasse, that bounds the number of points to be considered.
Hasse's theorem
Let E be an elliptic curve over the finite field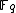 . Then the order of
. Then the order of  satisfies
satisfies
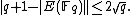
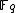 and testing which ones satisfy the Weierstrass form of the elliptic curve
and testing which ones satisfy the Weierstrass form of the elliptic curve
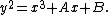
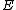 be the curve
be the curve 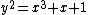 over
over 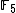 . To count points on
. To count points on 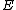 , we make a
, we make a
list of the possible values of , then of
, then of 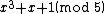 , then of the square
, then of the square
roots of
of  . This yields the points on
. This yields the points on 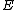 .
.
Therefore,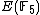 has order 9: the 8 points listed before and the point at infinity.
has order 9: the 8 points listed before and the point at infinity.
This algorithm requires running time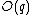 , because all the values of
, because all the values of 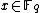 must be considered.
must be considered.
 by selecting random values of
by selecting random values of  until
until  is a square in
is a square in 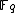 and then computing the square root of this value in order to get
and then computing the square root of this value in order to get 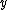 .
.
Hasse's theorem tells us that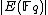 lies in the interval
lies in the interval 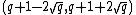 . Thus, by Lagrange's theorem
. Thus, by Lagrange's theorem
, finding a unique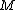 lying in this interval and satisfying
lying in this interval and satisfying 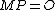 , results in finding the cardinality of
, results in finding the cardinality of 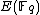 . The algorithm fails if there exist two integers
. The algorithm fails if there exist two integers 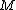 and
and 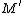 in the interval such that
in the interval such that 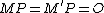 . In such a case it usually suffices to repeat the algorithm with another randomly chosen point in
. In such a case it usually suffices to repeat the algorithm with another randomly chosen point in  .
.
Trying all values of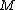 in order to find the one that satisfies
in order to find the one that satisfies 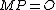 takes around
takes around 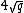 steps.
steps.
However, by applying the baby-step giant-step
algorithm to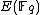 , we are able to speed this up to around
, we are able to speed this up to around 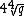 steps. The algorithm is as follows.
steps. The algorithm is as follows.
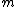 integer,
integer, 
2. FOR{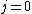 to
to 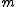 } DO
} DO
3.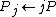
4. ENDFOR
5.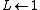
6.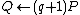
7. REPEAT compute the points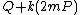
8. UNTIL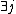 :
: 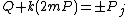 \\the
\\the  -coordinates are compared
-coordinates are compared
9.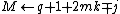 \\note
\\note 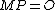
10. Factor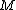 . Let
. Let 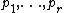 be the distinct prime factors of
be the distinct prime factors of 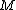 .
.
11. WHILE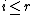 DO
DO
12. IF
13. THEN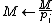
14. ELSE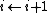
15. ENDIF
16. ENDWHILE
17.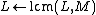 \\note
\\note 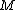 is the order of the point
is the order of the point 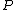
18. WHILE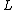 divides more than one integer
divides more than one integer 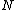 in
in 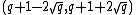
19. DO choose a new point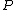 and go to 1.
and go to 1.
20. ENDWHILE
21. RETURN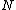 \\it is the cardinality of
\\it is the cardinality of 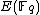
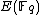 was achieved by René Schoof, who, in 1985, published the first deterministic polynomial time algorithm. Central to Schoof's algorithm are the use of division polynomials and Hasse's theorem, along with the Chinese remainder theorem
was achieved by René Schoof, who, in 1985, published the first deterministic polynomial time algorithm. Central to Schoof's algorithm are the use of division polynomials and Hasse's theorem, along with the Chinese remainder theorem
.
Schoof's insight exploits the fact that, by Hasse's Theorem, there is a finite range of possible values for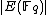 . It suffices to compute
. It suffices to compute 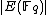 modulo an integer
modulo an integer 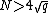 . This is achieved by computing
. This is achieved by computing 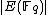 modulo primes
modulo primes  whose product exceeds
whose product exceeds 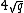 , and then applying the Chinese remainder theorem. The key to the algorithm is using the division polynomial
, and then applying the Chinese remainder theorem. The key to the algorithm is using the division polynomial 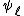 to efficiently compute
to efficiently compute 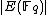 modulo
modulo  .
.
The running time of Schoof's Algorithm is polynomial in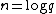 , with an asymptotic complexity of
, with an asymptotic complexity of 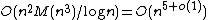 , where
, where 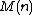 denotes the complexity of multiplication
denotes the complexity of multiplication
. Its space complexity is .
.
, followed by A. O. L. Atkin
devised improvements to Schoof's basic algorithm by making a distinction among the primes that are used. A prime
that are used. A prime 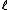 is called an Elkies prime if the characteristic equation of the Frobenius endomorphism,
is called an Elkies prime if the characteristic equation of the Frobenius endomorphism,  , splits over
, splits over 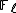 . Otherwise
. Otherwise 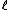 is called an Atkin prime. Elkies primes are the key to improving the asymptotic complexity of Schoof's algorithm. Information obtained from the Atkin primes permits a further improvement which is asymptotically negligible but can be quite important in practice. The modification of Schoof's algorithm to use Elkies and Atkin primes is known as the Schoof–Elkies–Atkin (SEA) algorithm.
is called an Atkin prime. Elkies primes are the key to improving the asymptotic complexity of Schoof's algorithm. Information obtained from the Atkin primes permits a further improvement which is asymptotically negligible but can be quite important in practice. The modification of Schoof's algorithm to use Elkies and Atkin primes is known as the Schoof–Elkies–Atkin (SEA) algorithm.
The status of a particular prime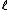 depends on the elliptic curve
depends on the elliptic curve 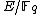 , and can be determined using the modular polynomial
, and can be determined using the modular polynomial
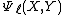 . If the univariate polynomial
. If the univariate polynomial 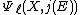 has a root in
has a root in 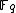 , where
, where 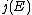 denotes the j-invariant
denotes the j-invariant
of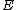 , then
, then  is an Elkies prime, and otherwise it is an Atkin prime. In the Elkies case, further computations involving modular polynomials are used to obtain a proper factor of the division polynomial
is an Elkies prime, and otherwise it is an Atkin prime. In the Elkies case, further computations involving modular polynomials are used to obtain a proper factor of the division polynomial 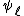 . The degree of this factor is
. The degree of this factor is 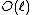 , whereas
, whereas 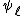 has degree
has degree 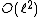 .
.
Unlike Schoof's algorithm, the SEA algorithm is typically implemented as a probabilistic algorithm
(of the Las Vegas
type), so that root-finding and other operations can be performed more efficiently. Its computational complexity is dominated by the cost of computing the modular polynomials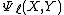 , but as these do not depend on
, but as these do not depend on 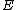 , they may be computed once and reused. Under the heuristic assumption that there are sufficiently many small Elkies primes, and excluding the cost of computing modular polynomials, the asymptotic running time of the SEA algorithm is
, they may be computed once and reused. Under the heuristic assumption that there are sufficiently many small Elkies primes, and excluding the cost of computing modular polynomials, the asymptotic running time of the SEA algorithm is 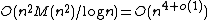 , where
, where 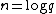 . Its space complexity is
. Its space complexity is  , but when precomputed modular polynomials are used this increases to
, but when precomputed modular polynomials are used this increases to 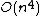 .
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, and more recently in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
and Digital Signature Authentication (See elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
and elliptic curve DSA
Elliptic Curve DSA
The Elliptic Curve Digital Signature Algorithm is a variant of the Digital Signature Algorithm which uses Elliptic curve cryptography.-Key and signature size comparison to DSA:...
). While in number theory they have important consequences in the solving of Diophantine equations, with respect to cryptography, they enable us to make effective use of the difficulty of the discrete logarithm problem (DLP) for the group
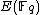 , of elliptic curves over a finite field
, of elliptic curves over a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
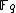 , where q = pk and p is a prime. The DLP, as it has come to be known, is a widely used approach to Public key cryptography, and the difficulty in solving this problem determines the level of security of the cryptosystem. This article covers algorithms to count points on elliptic curves over fields of large characteristic, in particular p > 3. For curves over fields of small characteristic more efficient algorithms based on p-adic methods exist.
, where q = pk and p is a prime. The DLP, as it has come to be known, is a widely used approach to Public key cryptography, and the difficulty in solving this problem determines the level of security of the cryptosystem. This article covers algorithms to count points on elliptic curves over fields of large characteristic, in particular p > 3. For curves over fields of small characteristic more efficient algorithms based on p-adic methods exist.Approaches to counting points on elliptic curves
There are several approaches to the problem. Beginning with the naive approach, we trace the developments up to Schoof's definitive work on the subject, while also listing the improvements to Schoof's algorithm made by Elkies (1990) and Atkin (1992).Several algorithms make use of the fact that groups of the form
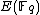 are subject to an important theorem due to Hasse, that bounds the number of points to be considered.
are subject to an important theorem due to Hasse, that bounds the number of points to be considered.Hasse's theorem
Let E be an elliptic curve over the finite field
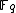 . Then the order of
. Then the order of  satisfies
satisfies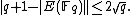
Naive approach
The naive approach to counting points, which is the least sophisticated, involves running through all the elements of the field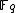 and testing which ones satisfy the Weierstrass form of the elliptic curve
and testing which ones satisfy the Weierstrass form of the elliptic curve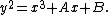
Example
Let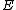 be the curve
be the curve 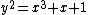 over
over 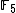 . To count points on
. To count points on 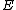 , we make a
, we make alist of the possible values of
 , then of
, then of 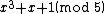 , then of the square
, then of the squareroots
 of
of  . This yields the points on
. This yields the points on 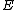 .
.  |
 |
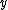 |
Points |
|---|---|---|---|
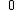 |
 |
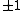 |
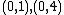 |
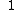 |
 |
 |
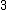 |
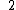 |
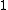 |
 |
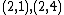 |
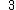 |
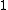 |
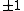 |
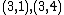 |
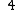 |
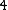 |
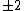 |
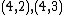 |
Therefore,
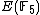 has order 9: the 8 points listed before and the point at infinity.
has order 9: the 8 points listed before and the point at infinity.This algorithm requires running time
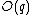 , because all the values of
, because all the values of 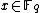 must be considered.
must be considered.Baby-step giant-step
An improvement in running time is obtained using a different approach: we pick an element by selecting random values of
by selecting random values of  until
until  is a square in
is a square in 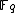 and then computing the square root of this value in order to get
and then computing the square root of this value in order to get 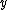 .
.Hasse's theorem tells us that
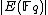 lies in the interval
lies in the interval 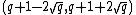 . Thus, by Lagrange's theorem
. Thus, by Lagrange's theoremLagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, finding a unique
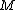 lying in this interval and satisfying
lying in this interval and satisfying 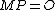 , results in finding the cardinality of
, results in finding the cardinality of 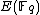 . The algorithm fails if there exist two integers
. The algorithm fails if there exist two integers 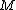 and
and 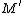 in the interval such that
in the interval such that 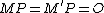 . In such a case it usually suffices to repeat the algorithm with another randomly chosen point in
. In such a case it usually suffices to repeat the algorithm with another randomly chosen point in  .
.Trying all values of
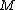 in order to find the one that satisfies
in order to find the one that satisfies 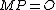 takes around
takes around 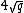 steps.
steps.However, by applying the baby-step giant-step
Baby-step giant-step
In group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm computing the discrete logarithm. The discrete log problem is of fundamental importance to the area of public key cryptography...
algorithm to
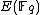 , we are able to speed this up to around
, we are able to speed this up to around 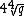 steps. The algorithm is as follows.
steps. The algorithm is as follows.The algorithm
1. choose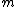 integer,
integer, 
2. FOR{
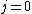 to
to 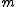 } DO
} DO3.
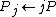
4. ENDFOR
5.
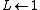
6.
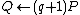
7. REPEAT compute the points
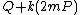
8. UNTIL
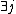 :
: 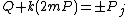 \\the
\\the  -coordinates are compared
-coordinates are compared9.
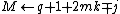 \\note
\\note 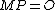
10. Factor
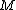 . Let
. Let 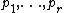 be the distinct prime factors of
be the distinct prime factors of 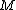 .
.11. WHILE
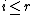 DO
DO12. IF

13. THEN
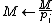
14. ELSE
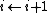
15. ENDIF
16. ENDWHILE
17.
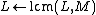 \\note
\\note 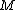 is the order of the point
is the order of the point 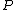
18. WHILE
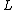 divides more than one integer
divides more than one integer 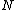 in
in 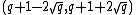
19. DO choose a new point
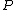 and go to 1.
and go to 1.20. ENDWHILE
21. RETURN
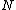 \\it is the cardinality of
\\it is the cardinality of 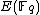
Schoof's algorithm
A theoretical breakthrough for the problem of computing the cardinality of groups of the type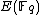 was achieved by René Schoof, who, in 1985, published the first deterministic polynomial time algorithm. Central to Schoof's algorithm are the use of division polynomials and Hasse's theorem, along with the Chinese remainder theorem
was achieved by René Schoof, who, in 1985, published the first deterministic polynomial time algorithm. Central to Schoof's algorithm are the use of division polynomials and Hasse's theorem, along with the Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
.
Schoof's insight exploits the fact that, by Hasse's Theorem, there is a finite range of possible values for
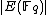 . It suffices to compute
. It suffices to compute 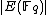 modulo an integer
modulo an integer 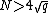 . This is achieved by computing
. This is achieved by computing 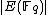 modulo primes
modulo primes  whose product exceeds
whose product exceeds 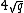 , and then applying the Chinese remainder theorem. The key to the algorithm is using the division polynomial
, and then applying the Chinese remainder theorem. The key to the algorithm is using the division polynomial 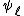 to efficiently compute
to efficiently compute 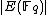 modulo
modulo  .
.The running time of Schoof's Algorithm is polynomial in
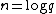 , with an asymptotic complexity of
, with an asymptotic complexity of 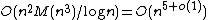 , where
, where 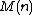 denotes the complexity of multiplication
denotes the complexity of multiplicationComputational complexity of mathematical operations
The following tables list the running time of various algorithms for common mathematical operations.Here, complexity refers to the time complexity of performing computations on a multitape Turing machine...
. Its space complexity is
 .
.Schoof–Elkies–Atkin algorithm
In the 1990s, Noam ElkiesNoam Elkies
Noam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
, followed by A. O. L. Atkin
A. O. L. Atkin
Arthur Oliver Lonsdale Atkin , who published under the name A. O. L. Atkin, was a Professor Emeritus of mathematics at the University of Illinois at Chicago. As an undergraduate during World War II, he worked at Bletchley Park cracking German codes. He received his Ph.D...
devised improvements to Schoof's basic algorithm by making a distinction among the primes
 that are used. A prime
that are used. A prime 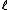 is called an Elkies prime if the characteristic equation of the Frobenius endomorphism,
is called an Elkies prime if the characteristic equation of the Frobenius endomorphism,  , splits over
, splits over 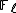 . Otherwise
. Otherwise 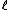 is called an Atkin prime. Elkies primes are the key to improving the asymptotic complexity of Schoof's algorithm. Information obtained from the Atkin primes permits a further improvement which is asymptotically negligible but can be quite important in practice. The modification of Schoof's algorithm to use Elkies and Atkin primes is known as the Schoof–Elkies–Atkin (SEA) algorithm.
is called an Atkin prime. Elkies primes are the key to improving the asymptotic complexity of Schoof's algorithm. Information obtained from the Atkin primes permits a further improvement which is asymptotically negligible but can be quite important in practice. The modification of Schoof's algorithm to use Elkies and Atkin primes is known as the Schoof–Elkies–Atkin (SEA) algorithm.The status of a particular prime
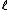 depends on the elliptic curve
depends on the elliptic curve 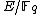 , and can be determined using the modular polynomial
, and can be determined using the modular polynomialClassical modular curve
In number theory, the classical modular curve is an irreducible plane algebraic curve given by an equationwhere for the j-invariant j,is a point on the curve. The curve is sometimes called X0, though often that is used for the abstract algebraic curve for which there exist various models...
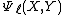 . If the univariate polynomial
. If the univariate polynomial 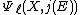 has a root in
has a root in 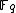 , where
, where 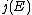 denotes the j-invariant
denotes the j-invariantJ-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
of
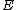 , then
, then  is an Elkies prime, and otherwise it is an Atkin prime. In the Elkies case, further computations involving modular polynomials are used to obtain a proper factor of the division polynomial
is an Elkies prime, and otherwise it is an Atkin prime. In the Elkies case, further computations involving modular polynomials are used to obtain a proper factor of the division polynomial 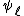 . The degree of this factor is
. The degree of this factor is 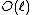 , whereas
, whereas 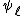 has degree
has degree 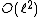 .
.Unlike Schoof's algorithm, the SEA algorithm is typically implemented as a probabilistic algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
(of the Las Vegas
Las Vegas algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the verity of the result; it gambles only with the resources...
type), so that root-finding and other operations can be performed more efficiently. Its computational complexity is dominated by the cost of computing the modular polynomials
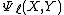 , but as these do not depend on
, but as these do not depend on 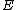 , they may be computed once and reused. Under the heuristic assumption that there are sufficiently many small Elkies primes, and excluding the cost of computing modular polynomials, the asymptotic running time of the SEA algorithm is
, they may be computed once and reused. Under the heuristic assumption that there are sufficiently many small Elkies primes, and excluding the cost of computing modular polynomials, the asymptotic running time of the SEA algorithm is 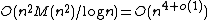 , where
, where 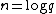 . Its space complexity is
. Its space complexity is  , but when precomputed modular polynomials are used this increases to
, but when precomputed modular polynomials are used this increases to 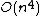 .
.See also
- Schoof's algorithmSchoof's algorithmSchoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography where it is important to know the number of points to judge the difficulty of solving the discrete logarithm problem in the group of...
- Elliptic curve cryptographyElliptic curve cryptographyElliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
- Baby-step giant-stepBaby-step giant-stepIn group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm computing the discrete logarithm. The discrete log problem is of fundamental importance to the area of public key cryptography...
- Public key cryptography
- Schoof–Elkies–Atkin algorithm
- Pollard rho
- Pollard kangaroo
- Elliptic curve primality provingElliptic curve primality provingElliptic Curve Primality Proving is a method based on elliptic curves to prove the primality of a number . It is a general-purpose algorithm, meaning it does not depend on the number being of a special form...

