Elliptic curve primality proving
Encyclopedia
Elliptic Curve Primality Proving (ECPP) is a method based on elliptic curves to prove the primality
of a number (see Elliptic curve primality testing
). It is a general-purpose algorithm
, meaning it does not depend on the number being of a special form. ECPP is currently in practice the fastest known algorithm for testing the primality of general numbers, but the worst-case execution time is not known. ECPP heuristically
runs in time: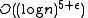
for some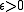
. This exponent may be decreased to 
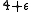for some versions by heuristic arguments. ECPP works the same way as most other primality test
s do, finding a group
and showing its size is such that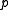
is prime. For ECPP the group is an elliptic curve over a finite set of quadratic forms such that 
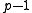is trivial to factor over the group.
ECPP generates an Atkin
-Goldwasser
-Kilian-Morain certificate
of primality by recursion
and then
attempts to verify the certificate. The step that takes the most CPU time is the certificate generation, because factoring over a class field must be performed. The certificate can be verified quickly, allowing a check of operation to take very little time.
In 2006 the largest prime that has been proved with ECPP is the 20,562-digit Mills' prime: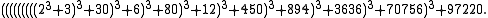
The distributed computation
with software by François Morain started in September 2005 and ended in June 2006. The cumulated time corresponds to one AMD Opteron 250 processor at 2.39 GHz for 2219 days (near 6 years).
As of 2011 the largest prime that has been proved with ECPP is the 26,643-digits LR prime. The distributed computation with software by François Morain started in January 2011 and ended in April 2011. The cumulated time corresponds to one processor for 2255 days (more than 6 years).
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
of a number (see Elliptic curve primality testing
Elliptic curve primality testing
Elliptic curve primality testing techniques are among the quickest and most widely used methods in primality proving. It is an idea forwarded by Shafi Goldwasser and Joe Kilian in 1986 and turned into an algorithm by A.O.L. Atkin the same year. The algorithm was altered and improved by several...
). It is a general-purpose algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, meaning it does not depend on the number being of a special form. ECPP is currently in practice the fastest known algorithm for testing the primality of general numbers, but the worst-case execution time is not known. ECPP heuristically
Heuristic argument
A heuristic argument is an argument that reasons from the value of a method or principle that has been shown by experimental investigation to be a useful aid in learning, discovery and problem-solving. A widely-used and important example of a heuristic argument is Occam's Razor....
runs in time:
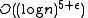
for some
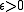. This exponent may be decreased to 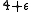for some versions by heuristic arguments. ECPP works the same way as most other primality testPrimality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
s do, finding a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and showing its size is such that
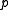is prime. For ECPP the group is an elliptic curve over a finite set of quadratic forms such that 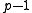is trivial to factor over the group.ECPP generates an Atkin
A. O. L. Atkin
Arthur Oliver Lonsdale Atkin , who published under the name A. O. L. Atkin, was a Professor Emeritus of mathematics at the University of Illinois at Chicago. As an undergraduate during World War II, he worked at Bletchley Park cracking German codes. He received his Ph.D...
-Goldwasser
Shafi Goldwasser
Shafrira Goldwasser is the RSA Professor of electrical engineering and computer science at MIT, and a professor of mathematical sciences at the Weizmann Institute of Science, Israel.-Biography:...
-Kilian-Morain certificate
Primality certificate
In mathematics and computer science, a primality certificate or primality proof is a succinct, formal proof that a number is prime. Primality certificates allow the primality of a number to be rapidly checked without having to run an expensive or unreliable primality test...
of primality by recursion
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
and then
attempts to verify the certificate. The step that takes the most CPU time is the certificate generation, because factoring over a class field must be performed. The certificate can be verified quickly, allowing a check of operation to take very little time.
In 2006 the largest prime that has been proved with ECPP is the 20,562-digit Mills' prime:
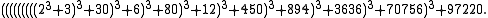
The distributed computation
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
with software by François Morain started in September 2005 and ended in June 2006. The cumulated time corresponds to one AMD Opteron 250 processor at 2.39 GHz for 2219 days (near 6 years).
As of 2011 the largest prime that has been proved with ECPP is the 26,643-digits LR prime. The distributed computation with software by François Morain started in January 2011 and ended in April 2011. The cumulated time corresponds to one processor for 2255 days (more than 6 years).
External links
- Elliptic Curves and Primality Proving by AtkinA. O. L. AtkinArthur Oliver Lonsdale Atkin , who published under the name A. O. L. Atkin, was a Professor Emeritus of mathematics at the University of Illinois at Chicago. As an undergraduate during World War II, he worked at Bletchley Park cracking German codes. He received his Ph.D...
and Morain. - Chris Caldwell, "Primality Proving 4.2: Elliptic curves and the ECPP test" at the Prime PagesPrime pagesThe Prime Pages is a website about prime numbers maintained by Chris Caldwell at the University of Tennessee at Martin.The site maintains the list of the "5,000 largest known primes", selected smaller primes of special forms, and many "top twenty" lists for primes of various forms...
. - François Morain, "The ECPP home page" (includes old ECPP software for some architectures).
- Marcel Martin, "Primo" (binary for Linux 64-bit)
- GMP-ECPP, a free ECPP implementation
- LiDIA, a free C++ library with ECPP support