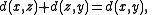Convex metric space
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, convex metric spaces are, intuitively, metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s with the property any "segment" joining two points in that space has other points in it besides the endpoints.
Formally, consider a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
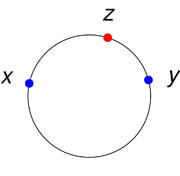
(X, d) and let x and y be two points in X. A point z in X is said to be between x and y if all three points are distinct, and
that is, the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
becomes an equality. A convex metric space is a metric space (X, d) such that, for any two distinct points x and y in X, there exists a third point z in X lying between x and y.
Metric convexity:
- does not imply convexity in the usual sense for subsets of Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(see the example of the rational numbers) - nor does it imply path-connectedness (see the example of the rational numbers)
- nor does it imply geodesic convexityGeodesic convexityIn mathematics — specifically, in Riemannian geometry — geodesic convexity is a natural generalization of convexity for sets and functions to Riemannian manifolds...
for Riemannian manifolds (consider, for example, the Euclidean plane with a closed disc removed).
Examples
- Euclidean spaces, that is, the usual three-dimensional space and its analogues for other dimensions, are convex metric spaces. Given any two distinct points
 and
and 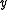 in such a space, the set of all points
in such a space, the set of all points  satisfying the above "triangle equality" forms the line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
satisfying the above "triangle equality" forms the line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
between and
and 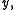 which always has other points except
which always has other points except  and
and 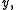 in fact, it has a continuum of points.
in fact, it has a continuum of points.
- Any convex setConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in a Euclidean space is a convex metric space with the induced Euclidean norm. For closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s the converseContrapositionIn traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
is also true: if a closed subset of a Euclidean space together with the induced distance is a convex metric space, then it is a convex set (this is a particular case of a more general statement to be discussed below). - A circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is a convex metric space, if the distance between two points is defined as the length of the shortest arc on the circle connecting them.
Metric segments
Let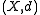 be a metric space (which is not necessarily convex). A subset
be a metric space (which is not necessarily convex). A subset 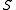 of
of 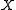 is called a metric segment between two distinct points
is called a metric segment between two distinct points  and
and 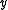 in
in 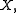 if there exists a closed interval
if there exists a closed interval 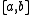 on the real line and an isometry
on the real line and an isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
such that
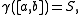
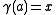 and
and 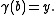
It is clear that any point in such a metric segment
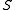 except for the "endponts"
except for the "endponts"  and
and 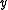 is between
is between  and
and 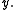 As such, if a metric space
As such, if a metric space 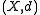 admits metric segments between any two distinct points in the space, then it is a convex metric space.
admits metric segments between any two distinct points in the space, then it is a convex metric space.The converse
Contraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
is not true, in general. The rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s form a convex metric space with the usual distance, yet there exists no segment connecting two rational numbers which is made up of rational numbers only. If however,
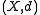 is a convex metric space, and, in addition, it is complete, one can prove that for any two points
is a convex metric space, and, in addition, it is complete, one can prove that for any two points 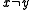 in
in 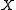 there exists a metric segment connecting them (which is not necessarily unique).
there exists a metric segment connecting them (which is not necessarily unique).Convex metric spaces and convex sets
As mentioned in the examples section, closed subsets of Euclidean spaces are convex metric spaces if and only if they are convex sets. It is then natural to think of convex metric spaces as generalizing the notion of convexity beyond Euclidean spaces, with usual linear segments replaced by metric segments.It is important to note, however, that metric convexity defined this way does not have one of the most important properties of Euclidean convex sets, that being that the intersection of two convex sets is convex. Indeed, as mentioned in the examples section, a circle, with the distance between two points measured along the shortest arc connecting them, is a (complete) convex metric space. Yet, if
 and
and 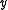 are two points on a circle diametrally opposite to each other, there exist two metric segments connecting them (the two arcs into which these points split the circle), and those two arcs are metrically convex, but their intersection is the set
are two points on a circle diametrally opposite to each other, there exist two metric segments connecting them (the two arcs into which these points split the circle), and those two arcs are metrically convex, but their intersection is the set 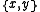 which is not metrically convex.
which is not metrically convex.