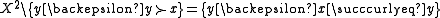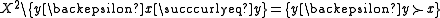Contour set
Encyclopedia
In mathematics
, contour sets generalize
and formalize
the everyday notions of
on pairs of elements of set

and an element of
of 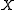

The upper contour set of is the set of all
is the set of all 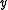 that are related to
that are related to  :
:
The lower contour set of is the set of all
is the set of all 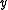 such that
such that  is related to them:
is related to them:
The strict upper contour set of is the set of all
is the set of all 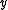 that are related to
that are related to  without
without  being in this way related to any of them:
being in this way related to any of them: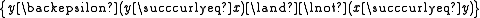
The strict lower contour set of is the set of all
is the set of all 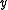 such that
such that  is related to them without any of them being in this way related to
is related to them without any of them being in this way related to  :
:
The formal expressions of the last two may be simplified if we have defined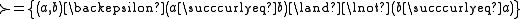
so that is related to
is related to  but
but 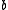 is not related to
is not related to  , in which case the strict upper contour set of
, in which case the strict upper contour set of  is
is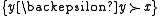
and the strict lower contour set of is
is
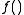 considered in terms of relation
considered in terms of relation  , reference to the contour sets of the function is implicitly to the contour sets of the implied relation
, reference to the contour sets of the function is implicitly to the contour sets of the implied relation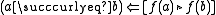
 , and the relation
, and the relation  . Then
. Then
Consider, more generally, the relation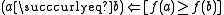
Then
It would be technically possible to define contour sets in terms of the relation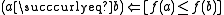
though such definitions would tend to confound ready understanding.
In the case of a real-valued function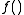 (whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation
(whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation
Note that the arguments to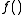 might be vector
might be vector
s, and that the notation
used might instead be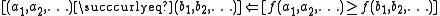
, the set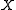 could be interpreted as a set of goods and services
could be interpreted as a set of goods and services
or of possible outcomes
, the relation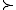 as strict preference
as strict preference
, and the relationship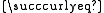 as weak preference. Then
as weak preference. Then
Such preferences might be captured by a utility
function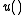 , in which case
, in which case
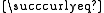 is a total order
is a total order
ing of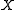 , the complement
, the complement
of the upper contour set is the strict lower contour set.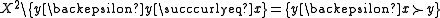
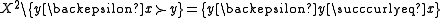
and the complement of the strict upper contour set is the lower contour set.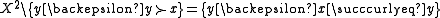
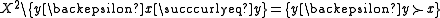
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, contour sets generalize
Generalization
A generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
and formalize
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
the everyday notions of
- everything superior to something
- everything superior or equivalent to something
- everything inferior to something
- everything inferior or equivalent to something.
Formal definitions
Given a relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
on pairs of elements of set


and an element
 of
of 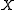

The upper contour set of
 is the set of all
is the set of all 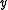 that are related to
that are related to  :
:
The lower contour set of
 is the set of all
is the set of all 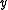 such that
such that  is related to them:
is related to them:
The strict upper contour set of
 is the set of all
is the set of all 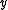 that are related to
that are related to  without
without  being in this way related to any of them:
being in this way related to any of them: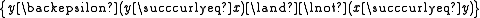
The strict lower contour set of
 is the set of all
is the set of all 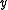 such that
such that  is related to them without any of them being in this way related to
is related to them without any of them being in this way related to  :
:
The formal expressions of the last two may be simplified if we have defined
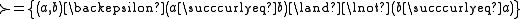
so that
 is related to
is related to  but
but 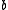 is not related to
is not related to  , in which case the strict upper contour set of
, in which case the strict upper contour set of  is
is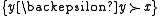
and the strict lower contour set of
 is
is
Contour sets of a function
In the case of a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
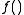 considered in terms of relation
considered in terms of relation  , reference to the contour sets of the function is implicitly to the contour sets of the implied relation
, reference to the contour sets of the function is implicitly to the contour sets of the implied relation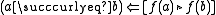
Arithmetic
Consider a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 , and the relation
, and the relation  . Then
. Then
- the upper contour set of
 would be the set of numbers that were greater than or equal to
would be the set of numbers that were greater than or equal to  ,
, - the strict upper contour set of
 would be the set of numbers that were greater than
would be the set of numbers that were greater than  ,
, - the lower contour set of
 would be the set of numbers that were less than or equal to
would be the set of numbers that were less than or equal to  , and
, and - the strict lower contour set of
 would be the set of numbers that were less than
would be the set of numbers that were less than  .
.
Consider, more generally, the relation
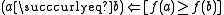
Then
- the upper contour set of
 would be the set of all
would be the set of all  such that
such that 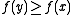 ,
, - the strict upper contour set of
 would be the set of all
would be the set of all 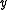 such that
such that 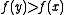 ,
, - the lower contour set of
 would be the set of all
would be the set of all 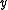 such that
such that 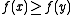 , and
, and - the strict lower contour set of
 would be the set of all
would be the set of all 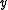 such that
such that 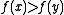 .
.
It would be technically possible to define contour sets in terms of the relation
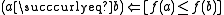
though such definitions would tend to confound ready understanding.
In the case of a real-valued function
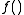 (whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation
(whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation
Note that the arguments to
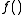 might be vector
might be vectorTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s, and that the notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
used might instead be
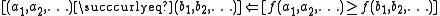
Economic
In economicsEconomics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, the set
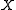 could be interpreted as a set of goods and services
could be interpreted as a set of goods and servicesGood (economics and accounting)
In economics, a good is something that is intended to satisfy some wants or needs of a consumer and thus has economic utility. It is normally used in the plural form—goods—to denote tangible commodities such as products and materials....
or of possible outcomes
Outcome (Game theory)
In game theory, an outcome is a set of moves or strategies taken by the players, or their payoffs resulting from the actions or strategies taken by all players. The two are complementary in that, given knowledge of the set of strategies of all players, the final state of the game is known, as are...
, the relation
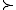 as strict preference
as strict preferencePreference
-Definitions in different disciplines:The term “preferences” is used in a variety of related, but not identical, ways in the scientific literature. This makes it necessary to make explicit the sense in which the term is used in different social sciences....
, and the relationship
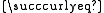 as weak preference. Then
as weak preference. Then
- the upper contour set of
 would be the set of all goods, services, or outcomes that were at least as desired as
would be the set of all goods, services, or outcomes that were at least as desired as  ,
, - the strict upper contour set of
 would be the set of all goods, services, or outcomes that were more desired than
would be the set of all goods, services, or outcomes that were more desired than  ,
, - the lower contour set of
 would be the set of all goods, services, or outcomes that were no more desired than
would be the set of all goods, services, or outcomes that were no more desired than  , and
, and - the strict lower contour set of
 would be the set of all goods, services, or outcomes that were less desired than
would be the set of all goods, services, or outcomes that were less desired than  .
.
Such preferences might be captured by a utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
function
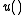 , in which case
, in which case
- the upper contour set of
 would be the set of all
would be the set of all 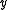 such that
such that 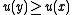 ,
, - the strict upper contour set of
 would be the set of all
would be the set of all 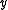 such that
such that  ,
, - the lower contour set of
 would be the set of all
would be the set of all 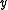 such that
such that 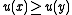 , and
, and - the strict lower contour set of
 would be the set of all
would be the set of all 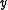 such that
such that  .
.
Complementarity
On the assumption that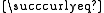 is a total order
is a total orderTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
ing of
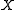 , the complement
, the complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the upper contour set is the strict lower contour set.
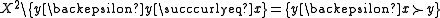
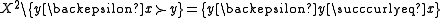
and the complement of the strict upper contour set is the lower contour set.