
Gimel function
Encyclopedia
In axiomatic set theory, the gimel function is the following function mapping cardinal number
s to cardinal numbers:
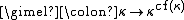
where cf denotes the cofinality
function; the gimel function is used for studying the continuum function
and the cardinal exponentiation function.
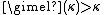 for all infinite cardinals κ by König's theorem
for all infinite cardinals κ by König's theorem
.
For regular cardinals
 ,
,
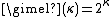 , and Easton's theorem
, and Easton's theorem
says we don't know much about the values of this function. For singular
 , upper bounds for
, upper bounds for 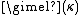 can be found from Shelah
can be found from Shelah
's PCF theory
.
The remaining rules hold whenever κ and λ are both infinite:
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s to cardinal numbers:
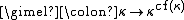
where cf denotes the cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
function; the gimel function is used for studying the continuum function
Continuum function
The continuum function is \kappa\mapsto 2^\kappa, i.e. raising 2 to the power of κ using cardinal exponentiation. Given a cardinal number, it is the cardinality of the power set of a set of the given cardinality.-See also:*Continuum hypothesis...
and the cardinal exponentiation function.
Values of the Gimel function
The gimel function has the property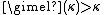 for all infinite cardinals κ by König's theorem
for all infinite cardinals κ by König's theoremKönig's theorem (set theory)
In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
.
For regular cardinals
 ,
,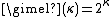 , and Easton's theorem
, and Easton's theoremEaston's theorem
In set theory, Easton's theorem is a result on the possible cardinal numbers of powersets. showed via forcing that...
says we don't know much about the values of this function. For singular
 , upper bounds for
, upper bounds for 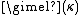 can be found from Shelah
can be found from ShelahSaharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
's PCF theory
PCF theory
PCF theory is the name of a mathematical theory, introduced by Saharon , that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well...
.
Reducing the exponentiation function to the gimel function
All cardinal exponentiation is determined (recursively) by the gimel function as follows.- If κ is an infinite successor cardinal then
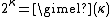
- If κ is a limit and the continuum function is eventually constant below κ then
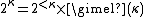
- If κ is a limit and the continuum function is not eventually constant below κ then
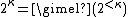
The remaining rules hold whenever κ and λ are both infinite:
- If ℵ0≤κ≤λ then κλ = 2λ
- If μλ≥κ for some μ<κ then κλ = μλ
- If κ> λ and μλ<κ for all μ<κ and cf(κ)≤λ then κλ = κcf(κ)
- If κ> λ and μλ<κ for all μ<κ and cf(κ)>λ then κλ = κ

