
Hyperfinite type II factor
Encyclopedia
In mathematics
, there are up to isomorphism exactly two hyperfinite type II factors; one infinite and one finite. Murray and von Neumann proved that up to isomorphism
there is a unique von Neumann algebra
that is a factor of type II1 and also hyperfinite; it is called the hyperfinite type II1 factor.
There are an uncountable number of other factors of type II1. Connes
proved that the infinite one is also unique.
infinite tensor product of a countable number of factors of type In with respect to their tracial states is the hyperfinite type II1 factor. When n=2, this is also sometimes called the Clifford algebra of an infinite separable Hilbert space.
dimensional factor in the following sense: it is contained in any other infinite dimensional factor, and any infinite dimensional factor contained in R is isomorphic to R.
The outer automorphism group of R is an infinite simple group with countable many conjugacy classes, indexed by pairs consisting of a positive integer p and a complex pth root of 1.
The projections of the hyperfinite II1 factor form a continuous geometry
.
one, up to isomorphism. It consists of those infinite square matrices with entries in the hyperfinite type II1 factor that define bounded operator
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there are up to isomorphism exactly two hyperfinite type II factors; one infinite and one finite. Murray and von Neumann proved that up to isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
there is a unique von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
that is a factor of type II1 and also hyperfinite; it is called the hyperfinite type II1 factor.
There are an uncountable number of other factors of type II1. Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
proved that the infinite one is also unique.
Constructions
- The von Neumann group algebra of a discrete group with the infinite conjugacy class propertyInfinite conjugacy class propertyIn mathematics, a group is said to have the infinite conjugacy class property, or to be an icc group, if the conjugacy class of every group element but the identity is infinite...
is a factor of type II1, and if the group is amenable and countable the factor is hyperfinite. There are many groups with these properties, as any locally finite groupLocally finite groupIn mathematics, in the field of group theory, a locally finite group is a type of group that can be studied in ways analogous to a finite group. Sylow subgroups, Carter subgroups, and abelian subgroups of locally finite groups have been studied....
is amenable. For example, the von Neumann group algebra of the infinite symmetric group of all permutations of a countable infinite set that fix all but a finite number of elements gives the hyperfinite type II1 factor. - The hyperfinite type II1 factor also arises from the group-measure space construction for ergodic free measure-preserving actions of countable amenable groups on probability spaces.
- The
infinite tensor product of a countable number of factors of type In with respect to their tracial states is the hyperfinite type II1 factor. When n=2, this is also sometimes called the Clifford algebra of an infinite separable Hilbert space.
- If p is any non-zero finite projection in a hyperfinite von Neumann algebra A of type II, then pAp is the hyperfinite type II1 factor. Equivalently the fundamental group of A is the group of all positive real numbers. This can often be hard to see directly. It is, however, obvious when A is the infinite tensor product of factors of type In, where n runs over all integers greater than 1 infinitely many times: just take p equivalent to an infinite tensor product of projections pn on which the tracial state is either 1 or
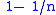 .
.
Properties
The hyperfinite II1 factor R is the unique smallest infinitedimensional factor in the following sense: it is contained in any other infinite dimensional factor, and any infinite dimensional factor contained in R is isomorphic to R.
The outer automorphism group of R is an infinite simple group with countable many conjugacy classes, indexed by pairs consisting of a positive integer p and a complex pth root of 1.
The projections of the hyperfinite II1 factor form a continuous geometry
Continuous geometry
In mathematics, continuous geometry is an analogue of complex projective geometry introduced by , where instead of the dimension of a subspace being in a discrete set 0, 1, ..., n, it can be an element of the unit interval [0,1]...
.
The infinite hyperfinite type II factor
While there are other factors of type II∞, there is a unique hyperfiniteHyperfinite
Hyperfinite may refer to:*Hyperfinite set*von Neumann algebra...
one, up to isomorphism. It consists of those infinite square matrices with entries in the hyperfinite type II1 factor that define bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s.

