
Interpretation (model theory)
Encyclopedia
In model theory
, interpretation of a structure
M in another structure N (typically of a different signature
) is a technical notion that approximates the idea of representing M inside N. For example every reduct
or definitional expansion of a structure N has an interpretation in N.
Many model-theoretic properties are preserved under interpretability. For example if the theory of N is stable
and M is interpretable in N, then the theory of M is also stable.
is a pair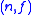 where
where
n is a natural number and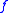 is a surjective map
is a surjective map
from a subset of
Nn onto M
such that the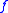 -preimage (more precisely the
-preimage (more precisely the 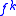 -preimage) of every set X ⊆ Mk definable
-preimage) of every set X ⊆ Mk definable
in M by a first-order formula without parameters
is definable (in N) by a first-order formula with parameters (or without parameters, respectively).
Since the value of n for an interpretation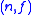 is often clear from context, the map
is often clear from context, the map 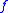 itself is also called an interpretation.
itself is also called an interpretation.
To verify that the preimage of every definable (without parameters) set in N is definable in M (with or without parameters), it is sufficient to check the preimages of the following definable sets:
In model theory
the term definable often refers to definability with parameters; if this convention is used, definability without parameters is expressed by the term 0-definable. Similarly, an interpretation with parameters may be referred to as simply an interpretation, and an interpretation without parameters as a 0-interpretation.
and M is interpreted in N, then one can naturally construct a composite interpretation of L in N.
If two structures M and N are interpreted in each other, then by combining the interpretations in two possible ways, one obtains an interpretation of each of the two structures in itself.
This observation permits to define an equivalence relation among structures, reminiscent of the homotopy equivalence among topological spaces.
Two structures M and N are bi-interpretable if there exists an interpretation of M in N and an interpretation of N in M such that the composite interpretations of M in itself and of N in itself are definable in M and in N, respectively (the composite interpretations being viewed as operations on M and on N).
In fact, this particular interpretation is often used to define the rational numbers.
To see that it is an interpretation (without parameters), one needs to check the following preimages of definable sets in Q:
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, interpretation of a structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
M in another structure N (typically of a different signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
) is a technical notion that approximates the idea of representing M inside N. For example every reduct
Reduct
In universal algebra and in model theory, a reduct of an algebraic structure is obtained by omitting some of the operations and relations of that structure...
or definitional expansion of a structure N has an interpretation in N.
Many model-theoretic properties are preserved under interpretability. For example if the theory of N is stable
Stable theory
In model theory, a complete theory is called stable if it does not have too many types. One goal of classification theory is to divide all complete theories into those whose models can be classified and those whose models are too complicated to classify, and to classify all models in the cases...
and M is interpretable in N, then the theory of M is also stable.
Definition
An interpretation of M in N with parameters (or without parameters, respectively)is a pair
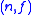 where
wheren is a natural number and
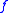 is a surjective map
is a surjective mapMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from a subset of
Nn onto M
such that the
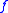 -preimage (more precisely the
-preimage (more precisely the 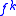 -preimage) of every set X ⊆ Mk definable
-preimage) of every set X ⊆ Mk definableDefinable set
In mathematical logic, a definable set is an n-ary relation on the domain of a structure whose elements are precisely those elements satisfying some formula in the language of that structure...
in M by a first-order formula without parameters
is definable (in N) by a first-order formula with parameters (or without parameters, respectively).
Since the value of n for an interpretation
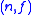 is often clear from context, the map
is often clear from context, the map 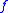 itself is also called an interpretation.
itself is also called an interpretation.To verify that the preimage of every definable (without parameters) set in N is definable in M (with or without parameters), it is sufficient to check the preimages of the following definable sets:
- the domain of N;
- the diagonal of N;
- every relation in the signature of N;
- the graphGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of every function in the signature of N.
In model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
the term definable often refers to definability with parameters; if this convention is used, definability without parameters is expressed by the term 0-definable. Similarly, an interpretation with parameters may be referred to as simply an interpretation, and an interpretation without parameters as a 0-interpretation.
Bi-interpretability
If L, M and N are three structures, L is interpreted in M,and M is interpreted in N, then one can naturally construct a composite interpretation of L in N.
If two structures M and N are interpreted in each other, then by combining the interpretations in two possible ways, one obtains an interpretation of each of the two structures in itself.
This observation permits to define an equivalence relation among structures, reminiscent of the homotopy equivalence among topological spaces.
Two structures M and N are bi-interpretable if there exists an interpretation of M in N and an interpretation of N in M such that the composite interpretations of M in itself and of N in itself are definable in M and in N, respectively (the composite interpretations being viewed as operations on M and on N).
Example
The partial map f from Z × Z onto Q which maps (x, y) to x/y provides an interpretation of the field Q of rational numbers in the ring Z of integers (to be precise, the interpretation is (2, f)).In fact, this particular interpretation is often used to define the rational numbers.
To see that it is an interpretation (without parameters), one needs to check the following preimages of definable sets in Q:
- the preimage of Q is defined by the formula φ(x, y) given by ¬ (y = 0);
- the preimage of the diagonal of Q is defined by the formula given by = ;
- the preimages of 0 and 1 are defined by the formulas φ(x, y) given by x = 0 and x = y;
- the preimage of the graph of addition is defined by the formula given by = ;
- the preimage of the graph of multiplication is defined by the formula given by = .

