Conjunctive query
Encyclopedia
In database theory
, a conjunctive query is a restricted form of first-order
queries. A large part of queries issued on relational database
s can be written as conjunctive queries, and large parts of other first-order queries can be written as conjunctive queries.
Conjunctive queries also have a number of desirable theoretical properties that larger classes of queries (e.g., the relational algebra
queries) do not share.
given by the set of
formulae that can be constructed from atomic formula
e using conjunction
and
existential quantification
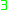, but not using disjunction 
, negation
,
or universal quantification
.
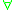Each such formula can be rewritten (efficiently) into an equivalent formula in prenex normal form
, thus this form is usually simply assumed.
Thus conjunctive queries are of the general form
,
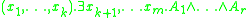with the free variables
being called distinguished variables, and the bound variables
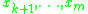being called undistinguished variables. 
are atomic formula
e. Conjunctive queries without distinguished variables are called boolean conjunctive queries
.
Conjunctive queries can express a large part of queries, which are frequently issued on relational database
s. To give an example, imagine a relational database for storing information about students, their address, the courses they visit and their gender. Finding all male students and their addresses who attend a course that is also attended by a female student is expressed by the following conjunctive query:
Note that since the only entity of interest is the male student and his address, these are the only distinguished variables, while the variables
, i.e. undistinguished.
(i.e.,
relational algebra queries that do not use the operations union or difference) and to select-from-where queries in SQL
in which the where-condition uses exclusively conjunctions of atomic equality conditions, i.e. conditions constructed from column names and constants using no comparison operators other than "=", combined using "and". Notably, this excludes the use of aggregation and subqueries. For example, the above query can be written as an SQL query of the conjunctive query fragment as
rules. Many authors in fact prefer the following datalog notation for the query above:
Although there are no quantifiers in this notation, variables appearing in the head of the rule are still implicitly universally quantified
, while variables only appearing in the body of the rule are still implicitly existentially quantified.
While any conjunctive query can be written as a datalog rule, not every datalog program can be written as a conjunctive query. In fact, only single rules over extensional predicate symbols can be easily rewritten as an equivalent conjunctive query. The problem of deciding whether for a given datalog program there is an equivalent nonrecursive program
(corresponding to a positive relational algebra query, or, equivalently, a formula of positive existential first-order logic
, or, as a special case, a conjunctive query) is known as the datalog boundedness problem and is undecidable.
include unions of conjunctive queries, which are equivalent to positive (i.e., negation
-free) relational algebra
, conjunctive queries extended by union and negation
, which by Codd's theorem
correspond to relational algebra
and first-order logic
, conjunctive queries with built-in predicates and conjunctive queries with aggregate function
s. The formal study of all of these extensions is justified by their application in relational databases and is in the realm of database theory
.
of evaluating conjunctive queries, two problems have to be distinguished. The first is the problem of evaluating a conjunctive query on a relational database
where both the query and the database are considered part of the input. The complexity of this problem is usually referred to as combined complexity, while the complexity of the problem of evaluating a query on a relational database, where the query is assumed fixed, is
called data complexity.
Conjunctive queries are NP-complete
with respect to combined complexity, while the data complexity of conjunctive queries is very low, in the parallel complexity class AC0
, which is contained in LOGSPACE and thus in polynomial time. The NP-hard
ness of conjunctive queries may appear surprising, since relational algebra
and SQL
strictly subsume the conjunctive queries and are thus at least as hard (in fact, relational algebra is PSPACE
-complete with respect to combined complexity and is therefore even harder under widely-held complexity-theoretic assumptions). However, in the usual application scenario, databases are large, while queries are very small, and the data complexity model may be appropriate studying and describing their difficulty.
in that many interesting problems that are computationally hard or undecidable for larger classes of queries are feasible for conjunctive queries. For example, consider the query containment problem. We write
for two database relations 
of the same schema
if and only if each tuple occurring in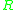
also occurs in 
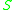. Given a query 
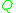and a relational database
instance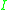
, we write the result relation of evaluating the query on the instance simply as 
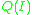. Given two queries 
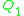and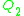 
and a database schema
, the query containment problem is the problem of deciding whether for all possible database instances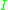
over the input database schema, 
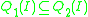. The main application of query containment is in query optimization: Deciding whether two queries are equivalent is possible by simply checking mutual containment.
The query containment problem is undecidable for relational algebra
and SQL
but is decidable and NP-complete
for conjunctive queries. In fact, it turns out that the query containment problem for conjunctive queries is exactly the same problem as the query evaluation problem. Since queries tend to be small, NP-completeness here is usually considered acceptable. The query containment problem for conjunctive queries is also equivalent to the constraint satisfaction problem
.
An important class of conjunctive queries that have polynomial-time combined complexity are the acyclic conjunctive queries. The query evaluation, and thus query containment, is LOGCFL
-complete and thus in polynomial time. Acyclicity of conjunctive queries is a structural property of queries that is defined with respect to the query's hypergraph
: a conjunctive query is acyclic if and only if it has hypertree-width 1. For the special case of conjunctive queries in which all relations used are binary, this notion corresponds to the treewidth of the dependency graph
of the variables in the query (i.e., the graph having the variables of the query as nodes and an undirected edge
between two variables if and only if there is an atomic formula 
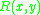or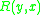 
in the query) and the conjunctive query is acyclic if and only if its dependency graph is acyclic
.
An important generalization of acyclicity is the notion of bounded hypertree-width, which is a measure of how close to acyclic a hypergraph is, analogous to bounded treewidth
in graphs
. Conjunctive queries of bounded tree-width have LOGCFL
combined complexity.
Unrestricted conjunctive queries over tree data (i.e., a relational database consisting of a binary child relation of a tree as well as unary relations for labeling the tree nodes) have polynomial time combined complexity.
Database theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
, a conjunctive query is a restricted form of first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
queries. A large part of queries issued on relational database
Relational database
A relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
s can be written as conjunctive queries, and large parts of other first-order queries can be written as conjunctive queries.
Conjunctive queries also have a number of desirable theoretical properties that larger classes of queries (e.g., the relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
queries) do not share.
Definition
The conjunctive queries are simply the fragment of first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
given by the set of
formulae that can be constructed from atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e using conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
andexistential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
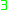, but not using disjunction , negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
,or universal quantification
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
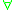.Each such formula can be rewritten (efficiently) into an equivalent formula in prenex normal form
Prenex normal form
A formula of the predicate calculus is in prenex normal form if it is written as a string of quantifiers followed by a quantifier-free part .Every formula in classical logic is equivalent to a formula in prenex normal form...
, thus this form is usually simply assumed.
Thus conjunctive queries are of the general form
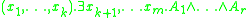,with the free variables
Free variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
being called distinguished variables, and the bound variablesFree variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
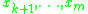being called undistinguished variables. are atomic formulaAtomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e. Conjunctive queries without distinguished variables are called boolean conjunctive queries
Boolean conjunctive query
In the theory of relational databases, a Boolean conjunctive query is a conjunctive query without distinguished predicates, i.e., a query in the form R_1 \wedge \cdots \wedge R_n, where each R_i is a relation symbol and each t_i is a tuple of variables and constants; the number of elements in t_i...
.
Conjunctive queries can express a large part of queries, which are frequently issued on relational database
Relational database
A relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
s. To give an example, imagine a relational database for storing information about students, their address, the courses they visit and their gender. Finding all male students and their addresses who attend a course that is also attended by a female student is expressed by the following conjunctive query:
(student, address) .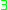 
(student2, course) .
attends(student, course) 
gender(student, 'male') 
attends(student2, course) 
gender(student2, 'female') 
lives(student, address)
Note that since the only entity of interest is the male student and his address, these are the only distinguished variables, while the variables
course, student2 are only existentially quantifiedExistential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
, i.e. undistinguished.
Relationship to other query languages
Conjunctive queries also correspond to select-project-join queries in relational algebraRelational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
(i.e.,
relational algebra queries that do not use the operations union or difference) and to select-from-where queries in SQL
SQL
SQL is a programming language designed for managing data in relational database management systems ....
in which the where-condition uses exclusively conjunctions of atomic equality conditions, i.e. conditions constructed from column names and constants using no comparison operators other than "=", combined using "and". Notably, this excludes the use of aggregation and subqueries. For example, the above query can be written as an SQL query of the conjunctive query fragment as
select l.student, l.address
from attends a1, gender g1,
attends a2, gender g2,
lives l
where a1.student=g1.student
and a2.student=g2.student
and l.student=g1.student
and a1.course=a2.course
and g1.gender='male'
and g2.gender='female';
Conjunctive queries and datalog
Besides their logical notation, conjunctive queries can also be written as datalogDatalog
Datalog is a query and rule language for deductive databases that syntactically is a subset of Prolog. Its origins date back to the beginning of logic programming, but it became prominent as a separate area around 1977 when Hervé Gallaire and Jack Minker organized a workshop on logic and databases...
rules. Many authors in fact prefer the following datalog notation for the query above:
result(student, address) :- attends(student, course), gender(student, male),
attends(student2, course), gender(student2, female),
lives(student, address).
Although there are no quantifiers in this notation, variables appearing in the head of the rule are still implicitly universally quantified
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
, while variables only appearing in the body of the rule are still implicitly existentially quantified.
While any conjunctive query can be written as a datalog rule, not every datalog program can be written as a conjunctive query. In fact, only single rules over extensional predicate symbols can be easily rewritten as an equivalent conjunctive query. The problem of deciding whether for a given datalog program there is an equivalent nonrecursive program
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
(corresponding to a positive relational algebra query, or, equivalently, a formula of positive existential first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, or, as a special case, a conjunctive query) is known as the datalog boundedness problem and is undecidable.
Extensions of conjunctive queries
Extensions of conjunctive queries capturing more expressive powerExpressive power
In computer science, the expressive power of a language describes the ideas expressible in that language.For example, the Web Ontology Language expression language profile lacks ideas which can be expressed in OWL2 RL . OWL2 EL may therefore be said to have less expressive power than OWL2 RL...
include unions of conjunctive queries, which are equivalent to positive (i.e., negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
-free) relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
, conjunctive queries extended by union and negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
, which by Codd's theorem
Codd's theorem
Codd's theorem states that relational algebra and the domain-independent relational calculus queries, two well-known foundational query languages for the relational model, are precisely equivalent in expressive power. That is, a database query can be formulated in one language if and only if it can...
correspond to relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
and first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, conjunctive queries with built-in predicates and conjunctive queries with aggregate function
Aggregate function
In computer science, an aggregate function is a function where the values of multiple rows are grouped together as input on certain criteria to form a single value of more significant meaning or measurement such as a set, a bag or a list....
s. The formal study of all of these extensions is justified by their application in relational databases and is in the realm of database theory
Database theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
.
Complexity of conjunctive queries
For the study of the computational complexityComputational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of evaluating conjunctive queries, two problems have to be distinguished. The first is the problem of evaluating a conjunctive query on a relational database
Relational database
A relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
where both the query and the database are considered part of the input. The complexity of this problem is usually referred to as combined complexity, while the complexity of the problem of evaluating a query on a relational database, where the query is assumed fixed, is
called data complexity.
Conjunctive queries are NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
with respect to combined complexity, while the data complexity of conjunctive queries is very low, in the parallel complexity class AC0
AC0
AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O and polynomial size, with unlimited-fanin AND gates and OR gates....
, which is contained in LOGSPACE and thus in polynomial time. The NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
ness of conjunctive queries may appear surprising, since relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
and SQL
SQL
SQL is a programming language designed for managing data in relational database management systems ....
strictly subsume the conjunctive queries and are thus at least as hard (in fact, relational algebra is PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
-complete with respect to combined complexity and is therefore even harder under widely-held complexity-theoretic assumptions). However, in the usual application scenario, databases are large, while queries are very small, and the data complexity model may be appropriate studying and describing their difficulty.
Formal properties of conjunctive queries
Conjunctive queries are one of the great success stories of database theoryDatabase theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
in that many interesting problems that are computationally hard or undecidable for larger classes of queries are feasible for conjunctive queries. For example, consider the query containment problem. We write
for two database relations of the same schemaDatabase schema
A database schema of a database system is its structure described in a formal language supported by the database management system and refers to the organization of data to create a blueprint of how a database will be constructed...
if and only if each tuple occurring in
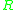also occurs in 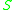. Given a query 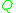and a relational databaseRelational database
A relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
instance
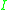, we write the result relation of evaluating the query on the instance simply as 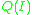. Given two queries 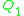and 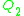and a database schemaDatabase schema
A database schema of a database system is its structure described in a formal language supported by the database management system and refers to the organization of data to create a blueprint of how a database will be constructed...
, the query containment problem is the problem of deciding whether for all possible database instances
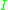over the input database schema, 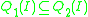. The main application of query containment is in query optimization: Deciding whether two queries are equivalent is possible by simply checking mutual containment.The query containment problem is undecidable for relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
and SQL
SQL
SQL is a programming language designed for managing data in relational database management systems ....
but is decidable and NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
for conjunctive queries. In fact, it turns out that the query containment problem for conjunctive queries is exactly the same problem as the query evaluation problem. Since queries tend to be small, NP-completeness here is usually considered acceptable. The query containment problem for conjunctive queries is also equivalent to the constraint satisfaction problem
Constraint satisfaction problem
Constraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
.
An important class of conjunctive queries that have polynomial-time combined complexity are the acyclic conjunctive queries. The query evaluation, and thus query containment, is LOGCFL
LOGCFL
In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter...
-complete and thus in polynomial time. Acyclicity of conjunctive queries is a structural property of queries that is defined with respect to the query's hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
: a conjunctive query is acyclic if and only if it has hypertree-width 1. For the special case of conjunctive queries in which all relations used are binary, this notion corresponds to the treewidth of the dependency graph
Dependency graph
In mathematics, computer science and digital electronics, a dependency graph is a directed graph representing dependencies of several objects towards each other...
of the variables in the query (i.e., the graph having the variables of the query as nodes and an undirected edge
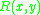between two variables if and only if there is an atomic formula or 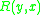in the query) and the conjunctive query is acyclic if and only if its dependency graph is acyclicGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
.
An important generalization of acyclicity is the notion of bounded hypertree-width, which is a measure of how close to acyclic a hypergraph is, analogous to bounded treewidth
Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
in graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. Conjunctive queries of bounded tree-width have LOGCFL
LOGCFL
In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter...
combined complexity.
Unrestricted conjunctive queries over tree data (i.e., a relational database consisting of a binary child relation of a tree as well as unary relations for labeling the tree nodes) have polynomial time combined complexity.
External links
- http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6V1G-43G4RRN-2&_user=5423704&_coverDate=05/28/2000&_rdoc=2&_fmt=summary&_orig=browse&_srch=doc-info(%23toc%235674%232000%23997609997%23255297%23FLP%23display%23Volume)&_cdi=5674&_sort=d&_docanchor=&_ct=8&_acct=C000007438&_version=1&_urlVersion=0&_userid=5423704&md5=adc35b17aaf28963cc6925a017813785Ullman, J. D. Information integration using logical views Theoretical Computer Science, 2000, 239, 189-210]
- Georg GottlobGeorg GottlobGeorg Gottlob FRS is an Oxford-based Austrian computer scientist who works in the areas of database theory, logic, and artificial intelligence.Gottlob obtained his PhD in computer science at Vienna University of Technology in 1981...
, Presentation on structural decomposition methods for the efficient evaluation of conjunctive queries (PDF)